今天来讨论多元函数求极值问题,在Logistic回归用牛顿迭代法求参数会用到,所以很有必要把它研究清楚。
回想一下,一元函数求极值问题我们是怎样做的?比如对于凹函数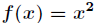 ,先求一阶导数,得
,先求一阶导数,得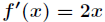 ,
,
由于极值处导数一定为零,但是导数等于零的点不一定就有极值,比如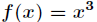 。所以还需要进一步判断,对
。所以还需要进一步判断,对
函数继续求二阶导得到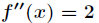 ,因为在驻点
,因为在驻点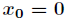 处二阶导数
处二阶导数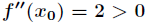 成立,所以
成立,所以
在 处取得极小值,二阶导数在这里的意义就是判断函数局部的凹凸性。
处取得极小值,二阶导数在这里的意义就是判断函数局部的凹凸性。
在多元函数中求极值的方法类似,只是在判断凹凸性这里引入了一个矩阵,叫做Hessian矩阵。
如果实值多元函数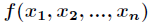 在定义域内二阶连续可导,那么我们求它的极值,首先对所有
在定义域内二阶连续可导,那么我们求它的极值,首先对所有
得到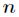 个方程如下
个方程如下
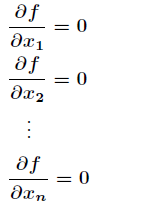
通过这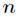 个方程可以解得驻点
个方程可以解得驻点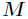 ,这个驻点是一个长度为
,这个驻点是一个长度为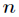 的一维向量。但是我们仅仅得到这个驻点,其实在这
的一维向量。但是我们仅仅得到这个驻点,其实在这
个驻点有3种情况,分别是:局部极大值,局部极小值和非极值。
所以接下来要做的事就是判断这个驻点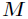 属于这3个中的哪一个。所以就引入了Hessian矩阵,也就是说它用来
属于这3个中的哪一个。所以就引入了Hessian矩阵,也就是说它用来
判断在多元函数的凹凸性问题。
Hessian矩阵是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率,常用于牛顿迭代法解决优化问题。
例如对于上面的多元函数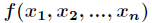 ,如果它的二阶偏导数都存在,那么Hessian矩阵如下
,如果它的二阶偏导数都存在,那么Hessian矩阵如下
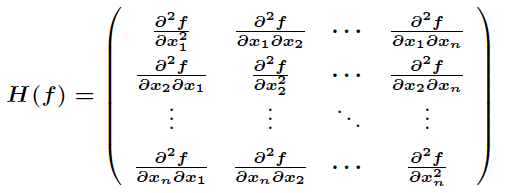
如果函数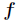 在定义域内二阶连续可导,那么
在定义域内二阶连续可导,那么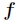 的Hessian矩阵
的Hessian矩阵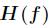 在定义域内为对称矩阵,因为如果函数
在定义域内为对称矩阵,因为如果函数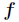 连
连
续,则二阶偏导数的求导顺序没有区别,即

有了Hessian矩阵,我们就可以判断上述极值的3种情况了,结论如下
(1)如果 是正定矩阵,则临界点
是正定矩阵,则临界点 处是一个局部极小值
处是一个局部极小值
(2)如果 是负定矩阵,则临界点
是负定矩阵,则临界点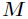 处是一个局部极大值
处是一个局部极大值
(3)如果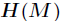 是不定矩阵,则临界点
是不定矩阵,则临界点
接下来继续学习如何判断一个矩阵是否是正定的,负定的,还是不定的。
一个最常用的方法就是顺序主子式。实对称矩阵

由于这个方法涉及到行列式的计算,比较麻烦! 对于实二次型矩阵还有一个方法,描述如下
实二次型矩阵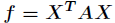 为正定二次型的充要条件是
为正定二次型的充要条件是

件是

拉格朗日乘数法
拉格朗日乘数法是用来求条件极值的,极值问题有两类,其一,求函数在给定区间上的极值,对自变量
没有其它要求,这种极值称为无条件极值。其二,对自变量有一些附加的约束条件限制下的极值,称为
条件极值。例如给定椭球

求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题,即在条件
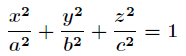
下,求 的最大值。
的最大值。
当然这个问题实际可以先根据条件消去 ,然后带入转化为无条件极值问题来处理。但是有时候这样做
,然后带入转化为无条件极值问题来处理。但是有时候这样做
很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。如下描述
求函数 在满足
在满足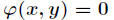 下的条件极值,可以转化为函数
下的条件极值,可以转化为函数
的无条件极值问题。如果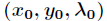 是函数
是函数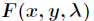 的驻点,则
的驻点,则 就是条件极值的嫌疑点。
就是条件极值的嫌疑点。
回到上面的题目,通过拉格朗日乘数法将问题转化为

对 求偏导得到
求偏导得到

联立前面三个方程得到 和
和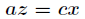 ,带入第四个方程解之
,带入第四个方程解之

带入解得最大体积为

拉格朗日乘数法对一般多元函数在多个附加条件下的条件极值问题也适用。例如
题目:求旋转抛物面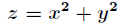 与平面
与平面 的交线上到坐标原点最近的点与最远的点。
的交线上到坐标原点最近的点与最远的点。
分析:设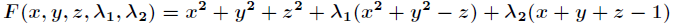 ,令
,令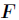 的所有
的所有
偏导数为零,得到
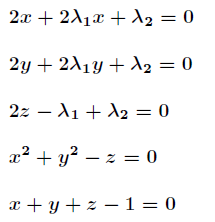
解得两个嫌疑点分别为
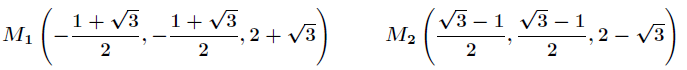
由于

所以,与原点最近的点是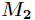 ,最远的点是
,最远的点是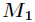 。
。
题目:求离散分布的最大熵。
分析:因为离散分布的熵表示如下
而约束条件为
要求函数
对所有的
计算出这
这说明所有的

因此,使用均匀分布可得到最大熵的值。




