前言
原题题目《瞿葩的数字游戏》T2-多边形数。
因为博客园标题不能太长所以压缩了一下。
题解
这道题目我是按表格中的列来考虑的,
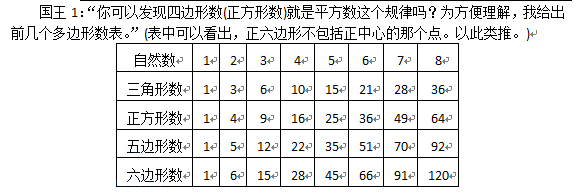
设读入的数字为(x),考虑上面的表格。
我们发现如果当前为第(k)列,那么该列每行之间都差了(1+2+dots+(k-1))。
于是我们暴力枚举列号,如果当前的(x)满足((x-k) \% (1+2+dots+(k-1))=0)的话,
显然(x)是珂以成为一个多边形数的。
设它为(n)边形,那么显然(n=(x-k) / (1+2+dots+(k-1))+2)
然后我们发现每一个边形数的第一个都是它自己,因此除了(2)以外不会有(poor),特判一下即可。
还有一个(1)也需要特殊处理,它应该输出(3)和(4)。
代码
#include <cstdio>
int read(){
int x = 0; int zf = 1; char ch = ' ';
while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') zf = -1, ch = getchar();
while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;
}
int main(){
int ng = read();
while (ng--){
int x = read(), ans1 = 0, ans2 = 0;
if (x == 1){puts("3 4"); continue;}
else if (x == 2){puts("Poor2"); continue;}
/*n边形数 k + (n - 2) * (1 + 2 + ... + k)*/
long long sum = 1;
for (int k = 2; ; ++k){
if (sum + k > x) break;
int lft = x - k;
if (!(lft % sum)){
int ans = lft / sum + 2;
if (ans >= 3){
if (ans < ans1 || (!ans1))
ans2 = ans1, ans1 = ans;
else if (ans < ans2 || (!ans2))
ans2 = ans;
}
}
sum += k;
}
if (ans1) printf("%d", ans1);
if (ans2) printf(" %d
", ans2);
else puts("");
}
return 0;
}