AcWing 848. 有向图的拓扑序列

题目传送门

一、理解与感悟

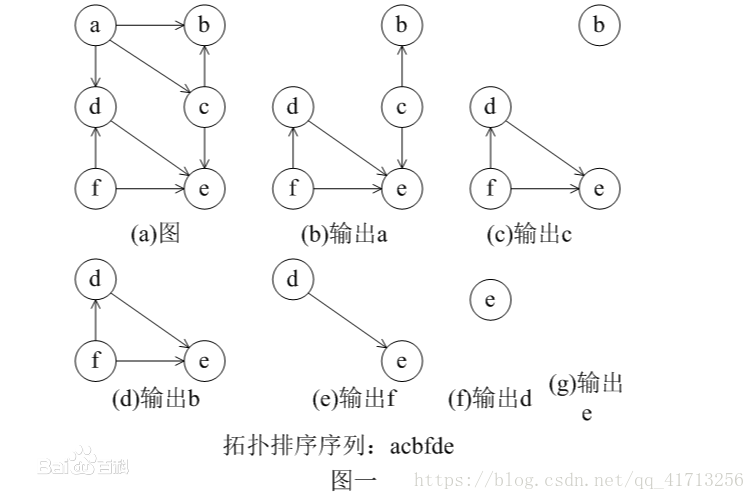
• 拓扑序：在一个有向图中，对所有的节点进行排序，要求没有一个节点指向它前面的节点。

• 有向无环图一定有拓扑序列,有向有环图一定没有拓扑序列。

• 出度：从节点出发，有几条边。 出度为零，表示是叶子节点。

• 入度：进入节点，有几条边。 入度为零，表示是根，应该排在拓扑序列最前面的位置。

二、完整代码

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int d[N], q[N]; //d[N]：入度,所有入度为零的点，可以排在当前最前面的位置。

//树和图的存储
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

//拓扑
bool topsort() {
    //初始化队列
    int hh = 0, tt = -1;

    //扫描所有入度为零的点入队列
    for (int i = 1; i <= n; i++)
        if (!d[i]) q[++tt] = i;

    //广度遍历
    while (hh <= tt) {
        int t = q[hh++];//队列头
        for (int i = h[t]; i != -1; i = ne[i]) {//遍历t的所有出边
            int j = e[i];
            if (--d[j] == 0)    //入度减1后，是不是为0
                q[++tt] = j;    //为0则入队列
        }
    }
    //如果一共n个结点进入过队列，则表示存在拓扑序
    return tt == n - 1;
}

int main() {
    //初始化为-1
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b);
        d[b]++;// 记录每个结点的入度
    }
    if (!topsort()) puts("-1");
    else {
        //队列次序其实就是拓扑序,这里就充分体现了利用数组模拟队列的优势，queue<int>就麻烦了。
        for (int i = 0; i < n; i++) printf("%d ", q[i]);
        puts("");
        //有向无环图的拓扑序是不唯一的
    }
    return 0;
}