CodeForces 608C Chain Reaction

#include <bits/stdc++.h> using namespace std; const int maxn = 1e6 + 50; int cov[100010]; ///覆盖个数 int sum[maxn]; struct node { int a, b; }; bool cmp(node A, node B) { return A.a < B.a; } node cnt[100010]; int vis[maxn]; int dp[100010][2]; int main() { // freopen("1.txt", "r", stdin); int n; scanf("%d", &n); for(int i = 1; i <= n; i++) scanf("%d %d", &cnt[i].a, &cnt[i].b), vis[cnt[i].a] = 1; sum[0] = vis[0]; for(int i = 1; i <= (1e6); i++) sum[i] = sum[i - 1] + vis[i]; ///求前缀和 sort(cnt + 1, cnt + n + 1, cmp); for(int i = 1; i <= n; i++) ///相当于离散化一下 { // int tmp = (cnt[i].a - cnt[i].b - 1 > 0 ? cnt[i].a - cnt[i].b - 1 : 0); if(cnt[i].a - cnt[i].b - 1 >= 0) cov[i] = sum[cnt[i].a] - sum[cnt[i].a - cnt[i].b - 1]; ///覆盖的区间个数 + 1 else cov[i] = sum[cnt[i].a]; } for(int i = 1; i <= n; i++) { dp[i][0] = dp[i - cov[i]][0] + 1; ///第i灯亮,则跳到它所覆盖区间之前的灯 dp[i][1] = max(dp[i - 1][0], dp[i - 1][1]); ///第i灯灭,则前一个灯的情况取最大值 } printf("%d ", n - max(dp[n][0], dp[n][1])); return 0; } /* 11 110 90 100 70 90 10 80 10 70 1 60 1 50 10 40 1 30 1 10 1 20 1 */
AC自动机+DP,过后再补。。。
01背包放置有顺序,状压处理不了,贪心来处理。

#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> using namespace std; const int maxn = 1e3 + 50; struct node { int a, b, c; friend bool operator < (node A, node B) { return B.b * A.c < A.b * B.c; } }; node pro[maxn]; int dp[3333]; int main() { int T; scanf("%d", &T); while(T--) { int n, t; scanf("%d %d", &n, &t); for(int i = 1; i <= n; i++) scanf("%d %d %d", &pro[i].a, &pro[i].b, &pro[i].c); sort(pro + 1, pro + n + 1); memset(dp, -1, sizeof(dp)); dp[0] = 0; int ans = 0; for(int i = 1; i <= n; i++) { for(int j = t; j >= pro[i].c; j--) { if(dp[j - pro[i].c] != -1) dp[j] = max(dp[j], dp[j - pro[i].c] + pro[i].a - pro[i].b * j); ans = max(ans, dp[j]); } } printf("%d ", ans); } }
枚举每一位的贡献,![]()

#include <cstdio> #include <algorithm> #include <map> #include <cstring> using namespace std; typedef long long ll; map<ll, ll> mp; const int maxn = 111111; const ll mod = 1e9 + 7; ll a[maxn]; ll mi[maxn]; int main() { int T; scanf("%d", &T); mi[0] = 1; for(int i = 1; i < maxn; i++) mi[i] = mi[i - 1] * 2LL % mod; while(T--) { mp.clear(); int n; scanf("%d", &n); for(int i = 1; i <= n; i++) scanf("%I64d", &a[i]); ll ans = 0; for(int i = 1; i <= n; i++) { if(mp.count(a[i])) ans = (ans + (mi[i - 1] + mod - mp[a[i]] ) % mod * mi[n - i] % mod * a[i] % mod) % mod; else ans = (ans + (mi[i - 1]) * mi[n - i] % mod * a[i] % mod) % mod; mp[a[i]] = (mp[a[i]] + mi[i - 1]) % mod; } printf("%I64d ", ans); } return 0; }

#include <bits/stdc++.h> using namespace std; const int maxn = 1e5+50; typedef long long ll; vector<int> g[maxn]; ///加边 int cnt, h[maxn]; struct edge { int to, pre, v; } e[maxn << 1]; void init() { cnt = 0; memset(h, 0, sizeof(h)); } void add(int from, int to, int v) { cnt++; e[cnt].pre = h[from]; ///5-->3-->1-->0 e[cnt].to = to; e[cnt].v = v; h[from] = cnt; } ///LCA int dist[maxn]; int dep[maxn]; int anc[maxn][33]; ///2分的父亲节点 void dfs(int u, int fa) { for(int i = h[u]; i; i = e[i].pre) { int v = e[i].to; if(v == fa) continue; dist[v] = dist[u] + e[i].v; dep[v] = dep[u] + 1; anc[v][0] = u; dfs(v, u); } } void LCA_init(int n) { for(int j = 1; (1 << j) < n; j++) for(int i = 1; i <= n; i++) if(anc[i][j-1]) anc[i][j] = anc[anc[i][j-1]][j-1]; } int LCA(int u, int v) { int log; if(dep[u] < dep[v]) swap(u, v); for(log = 0; (1 << log) < dep[u]; log++); for(int i = log; i >= 0; i--) if(dep[u] - (1 << i) >= dep[v]) u = anc[u][i]; if(u == v) return u; for(int i = log; i >= 0; i--) if(anc[u][i] && anc[u][i] != anc[v][i]) u = anc[u][i], v = anc[v][i]; return anc[u][0]; } int main() { int T; scanf("%d", &T); while(T--) { init(); int n,m; scanf("%d %d",&n,&m); for(int i=1;i<n;i++) { int u,v,w; scanf("%d %d %d",&u,&v,&w); add(u,v,w),add(v,u,w); } for(int i=1;i<=m;i++) { g[i].clear(); int G; scanf("%d",&G); int x; while(G--) { scanf("%d",&x); g[i].push_back(x); } sort(g[i].begin(),g[i].end()); g[i].end() = g[i].erase(unique(g[i].begin(),g[i].end()),g[i].end()); } dist[1] = 0; ///定义根节点 dfs(1,0); LCA_init(n); int Q; scanf("%d",&Q); while(Q--) { int u,v; scanf("%d %d",&u,&v); int ans = 1e9; for(int i=0;i<g[u].size();i++) { for(int j=0;j<g[v].size();j++) { int p = g[u][i],q = g[v][j]; ans = min(ans,dist[p]+dist[q]-2*dist[LCA(p,q)]); } } printf("%d ",ans); } } return 0; }
Minimum spanning tree for each edge

#include <bits/stdc++.h> using namespace std; const int maxn = 2e5+50; typedef long long ll; ///加边 int cnt, h[maxn]; struct edge { int id; int to, pre, v; int a, b; friend bool operator < (edge A, edge B) { return A.v < B.v; } } e[maxn << 1], ms[maxn]; void init() { cnt = 0; memset(h, 0, sizeof(h)); } void add(int from, int to, int v) { cnt++; e[cnt].pre = h[from]; ///5-->3-->1-->0 e[cnt].to = to; e[cnt].v = v; h[from] = cnt; } ///LCA int dist[maxn]; int dep[maxn]; int anc[maxn][33]; ///2分的父亲节点 int MAX[maxn][33]; ///记录路径上的最大值 ///附加信息 void dfs(int u, int fa) { for(int i = h[u]; i; i = e[i].pre) { int v = e[i].to; if(v == fa) continue; dist[v] = dist[u] + e[i].v; dep[v] = dep[u] + 1; anc[v][0] = u; MAX[v][0] = e[i].v; ///附加信息 dfs(v, u); } } void LCA_init(int n) { for(int j = 1; (1 << j) < n; j++) for(int i = 1; i <= n; i++) { if(anc[i][j-1]) { anc[i][j] = anc[anc[i][j-1]][j-1]; MAX[i][j] = max(MAX[i][j-1], MAX[anc[i][j-1]][j-1]); ///附加信息 } } } int LCA(int u, int v) { int ret = 0; int log; if(dep[u] < dep[v]) swap(u, v);///u高1 v低2,u低2 v高1 for(log = 0; (1 << log) < dep[u]; log++); for(int i = log; i >= 0; i--) if(dep[u] - (1 << i) >= dep[v]) { ret = max(ret, MAX[u][i]); ///附加信息 u = anc[u][i]; } if(u == v) return ret; ///附加信息 for(int i = log; i >= 0; i--) if(anc[u][i] && anc[u][i] != anc[v][i]) { ret = max(ret, max(MAX[u][i], MAX[v][i])); ///附加信息 u = anc[u][i]; v = anc[v][i]; } return max(ret, max(MAX[u][0], MAX[v][0])); ///附加信息 } int pre[maxn]; int Find(int x) { return x == pre[x] ? x : (pre[x] = Find(pre[x])); } ll MST(int n, int m) { ll mincost = 0; for(int i = 1; i <= n; i++) pre[i] = i; for(int i = 1; i <= m; i++) { int a = Find(ms[i].a); int b = Find(ms[i].b); if(a != b) { pre[a] = b; add(ms[i].a, ms[i].b, ms[i].v); add(ms[i].b, ms[i].a, ms[i].v); mincost += ms[i].v; } } return mincost; } ll ans[maxn]; int main() { init(); int n, m; scanf("%d %d",&n, &m); for(int i = 1; i <= m; i++) { ms[i].id = i; scanf("%d %d %d", &ms[i].a, &ms[i].b, &ms[i].v); } sort(ms + 1, ms + m + 1); ll mincost = MST(n, m); dfs(1, -1); LCA_init(n); for(int i = 1; i <= m; i++) { ans[ms[i].id] = mincost - LCA(ms[i].a, ms[i].b) + ms[i].v; } for(int i = 1; i <= m; i++) { printf("%I64d ", ans[i]); } return 0; }
自己的做法做完后发现要超时,发现网上的题解 全是主席树 + LCA,绝望之际,发现学姐的做法,正是LCA修改部分的真谛,LCA的修改信息能衍生出好多题目来,让我想起来 网络流模板里的修改,能修改了模板,才能掌握了算法。

#include <bits/stdc++.h> using namespace std; const int maxn = 1e5+50; typedef long long ll; vector<int> g[maxn]; vector<int> mer[maxn][33]; ///加边 int cnt, h[maxn]; struct edge { int to, pre, v; } e[maxn << 1]; void init() { cnt = 0; memset(h, 0, sizeof(h)); } void add(int from, int to, int v) { cnt++; e[cnt].pre = h[from]; ///5-->3-->1-->0 e[cnt].to = to; e[cnt].v = v; h[from] = cnt; } ///LCA int dist[maxn]; int dep[maxn]; int anc[maxn][33]; ///父亲节点 void Merge(vector <int> &a, vector <int> b) { for(int i = 0; i < min(10, (int)b.size()); i++) a.push_back(b[i]); sort(a.begin(), a.end()); int len = unique(a.begin(), a.end()) - a.begin(); ///虽然不会有重复的节点编号,但是比如 a中3号之前已经被放到过be了 a.resize(min(len, 10)); ///revize重新分配n块,并保留前n个数字 } void dfs(int u, int fa) { for(int i = h[u]; i; i = e[i].pre) { int v = e[i].to; if(v == fa) continue; dist[v] = dist[u] + e[i].v; dep[v] = dep[u] + 1; anc[v][0] = u; Merge(mer[v][0], g[v]); Merge(mer[v][0], g[u]); ///合并我和父亲节点的值 dfs(v, u); } } void LCA_init(int n) { for(int j = 1; (1 << j) < n; j++) for(int i = 1; i <= n; i++) if(anc[i][j-1]) { anc[i][j] = anc[anc[i][j-1]][j-1]; Merge(mer[i][j], mer[i][j-1]); Merge(mer[i][j], mer[anc[i][j-1]][j-1]); } } vector<int> ans; int LCA(int u, int v) { int log; if(dep[u] < dep[v]) swap(u, v); for(log = 0; (1 << log) < dep[u]; log++); for(int i = log; i >= 0; i--) if(dep[u] - (1 << i) >= dep[v]) { Merge(ans, mer[u][i]); u = anc[u][i]; } if(u == v) { Merge(ans, g[u]); return u; } for(int i = log; i >= 0; i--) if(anc[u][i] && anc[u][i] != anc[v][i]) { Merge(ans, mer[u][i]); Merge(ans, mer[v][i]); u = anc[u][i], v = anc[v][i]; } Merge(ans, mer[u][0]); Merge(ans, mer[v][0]); return anc[u][0]; } int main() { int n, m, q; scanf("%d %d %d", &n, &m, &q); init(); for(int i = 1; i < n; i++) { int u, v; scanf("%d %d", &u, &v); add(u, v, 1), add(v, u, 1); } for(int i = 1; i <= m; i++) { int x; scanf("%d", &x); g[x].push_back(i); } for(int i = 1; i <= n; i++) { sort(g[i].begin(), g[i].end()); if(g[i].size() > 10) g[i].resize(10); ///很关键 } dfs(1, -1); LCA_init(n); ///千万记得初始化!!!!! while(q--) { int u, v, a; scanf("%d %d %d", &u, &v, &a); ans.clear(); LCA(u, v); printf("%d ", min(a, (int)ans.size())); for(int i = 0; i < min(a, (int)ans.size()); i++) { printf("%d ", ans[i]); } printf(" "); } return 0; }

#include <bits/stdc++.h> using namespace std; const int maxn = 1e5+50; typedef long long ll; vector<int> g[maxn]; ///加边 int cnt, h[maxn]; struct edge { int to, pre, v; } e[maxn << 1]; void init() { cnt = 0; memset(h, 0, sizeof(h)); } void add(int from, int to, int v) { cnt++; e[cnt].pre = h[from]; ///5-->3-->1-->0 e[cnt].to = to; e[cnt].v = v; h[from] = cnt; } ///LCA int dist[maxn]; int dep[maxn]; int anc[maxn][33]; ///2分的父亲节点 int num[maxn]; void dfs(int u, int fa) { num[u]++; for(int i = h[u]; i; i = e[i].pre) { int v = e[i].to; if(v == fa) continue; dist[v] = dist[u] + e[i].v; dep[v] = dep[u] + 1; anc[v][0] = u; dfs(v, u); num[u] += num[v]; } } void LCA_init(int n) { for(int j = 1; (1 << j) < n; j++) for(int i = 1; i <= n; i++) if(anc[i][j-1]) anc[i][j] = anc[anc[i][j-1]][j-1]; } int LCA(int u, int v) { int log; if(dep[u] < dep[v]) swap(u, v); for(log = 0; (1 << log) < dep[u]; log++); for(int i = log; i >= 0; i--) if(dep[u] - (1 << i) >= dep[v]) u = anc[u][i]; if(u == v) return u; for(int i = log; i >= 0; i--) if(anc[u][i] && anc[u][i] != anc[v][i]) u = anc[u][i], v = anc[v][i]; return anc[u][0]; } int calc(int u, int d) ///计算u节点向上深度为d的节点编号 { for(int i = 30; i >= 0; i--) { if(dep[u] - (1 << i) >= d) u = anc[u][i]; } return u; } int main() { int n; scanf("%d", &n); init(); for(int i = 1; i < n; i++) { int a, b; scanf("%d %d", &a, &b); add(a, b, 1), add(b, a, 1); } memset(num, 0, sizeof(num)); dfs(1, -1); LCA_init(n); int m; scanf("%d", &m); for(int i = 1; i <= m; i++) { int u, v; scanf("%d %d", &u, &v); int lca = LCA(u, v); if(u == v) { printf("%d ", n); continue; } if(dep[u] == dep[v]) { int tmp = dep[lca] + 1; int fu = calc(u, tmp); int fv = calc(v, tmp); printf("%d ", n - num[fu] - num[fv]); } else { int dist = dep[u] + dep[v] - 2 * dep[lca]; if(dist % 2) { puts("0"); continue; } if(dep[v] < dep[u]) swap(u, v); int mid = calc(v, dist / 2 - dep[u] + 2 * dep[lca]); int k = calc(v, dist / 2 - dep[u] + 2 * dep[lca] + 1); printf("%d ", num[mid] - num[k]); } } return 0; }
CHD校赛
我发现我每次比赛WA上几发后(尤其是在别人都会的题目上),心情就会很暴躁,不能太着急,可能是算法没选对。
L题比赛时候gf的策略是我现在的钱数掉在哪段区间,离哪个端点最近就选那个钱数,我没法证明正确性,不过也AC了,也尝试了dfs,一直写的有点搓。看了牛客代码,很精致。

#include <iostream> #include <algorithm> #include <cmath> using namespace std; int ans = 0; void dfs(int res, int mi, int num)///剩余钱数 幂 货币数量 { int cur = pow(9, mi); if(cur == 1) { ans = min(ans, num + res); return; } dfs(res % cur, mi - 1, num + res / cur); dfs(cur - res % cur, mi - 1, num + res / cur + 1); } int main() { int T; cin >> T; while(T--) { ans = 1e9 + 5; int n; cin >> n; dfs(n, 4, 0); cout << ans << endl; } return 0; }
得知这道题是费用流,我就在想从正面怎么做。
正面的话,求的是总的最小面积,如把面积当成费用的话,应该求的是一股水流中的最大值,而不是费用和,拿网络流没法做。
看了题解后,画出此图
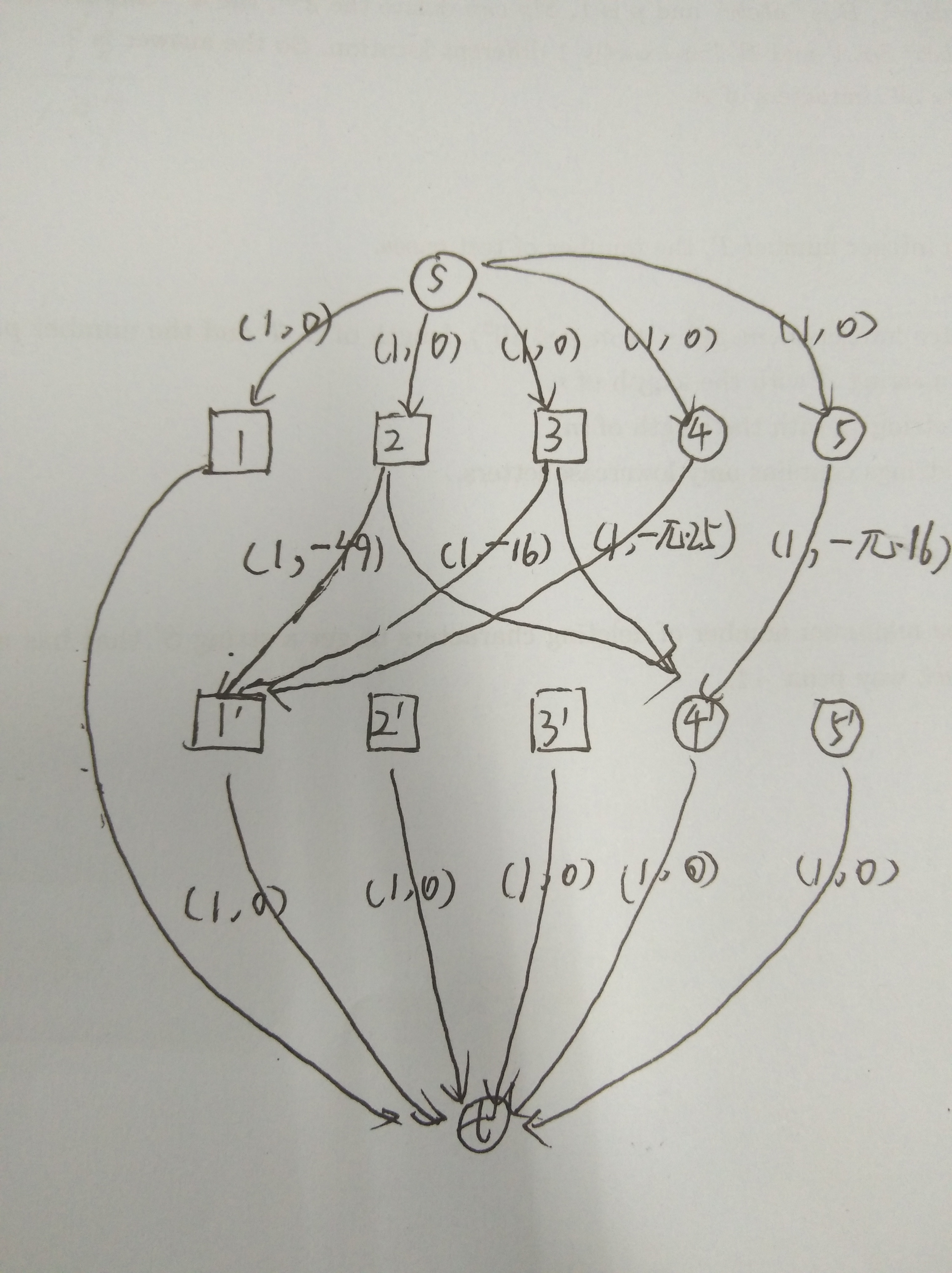
它首先拆点,然后s先向每个图形连一条容量为1,费用为0(即(1,0))的边,表示有这么多的图形。 每个复制点再向汇点t连一条(1,0)边,这条边保证与每个图形直接嵌套的最多有一个,然后每个原先的点再向 t 连一条(1,0)的边(表示我不嵌套也可以,其实这些边我觉得不连也是可以的),然后如果2能放到1里,连一条(1,-1*面积)的边。画完所有边后,跑最小费用流,得到的负值取正就是我嵌套到别人身体里的最大面积,最后用总面积减去就可以了。
代码还在一直超时。。。,和nps要他的代码看看。。。
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<set> #include<map> #include<queue> #include<stack> #include<vector> using namespace std; typedef long long ll; typedef pair<double,int> P; #define PI acos(-1.0) const int maxn=505,maxm=1e5+100,inf=0x3f3f3f3f,mod=1e9+7; const ll INF=1e18+7; const double eps=0.000001; struct edge { int from,to; int cap; double cost; int rev; }; int NN; vector<edge>G[maxn]; double h[maxn]; ///顶点的势,取h(u)=(s到u的最短距离),边e=(u,v)的长度变成d`(e)=d(e)+h(u)-h(v)>=0 double dist[maxn]; int prevv[maxn],preve[maxn];///前驱结点和对应的边 void addedge(int u,int v,int cap,double cost) { edge e; e.from=u,e.to=v,e.cap=cap,e.cost=cost,e.rev=G[v].size(); G[u].push_back(e); e.from=v,e.to=u,e.cap=0,e.cost=-cost,e.rev=G[u].size()-1; G[v].push_back(e); } double min_cost_flow(int s,int t,int f) { double res=0.0; NN = 500; fill(h,h+NN,0.0); while(f>0) { priority_queue<P,vector<P>,greater<P> >q; fill(dist,dist+NN,inf); dist[s]=0.0; q.push(P(dist[s],s)); while(!q.empty()) { P p=q.top(); q.pop(); int u=p.second; if(dist[u]<p.first) continue; for(int i=0; i<G[u].size(); i++) { edge e=G[u][i]; if(e.cap>0&&dist[e.to]-(dist[u]+e.cost+h[u]-h[e.to])>=eps) { dist[e.to]=dist[u]+e.cost+h[u]-h[e.to]; prevv[e.to]=u; preve[e.to]=i; q.push(P(dist[e.to],e.to)); } } } if(fabs(dist[t]-inf)<=eps) return res; for(int i=0; i<NN; i++) h[i]+=dist[i]; int d=f; for(int i=t; i!=s; i=prevv[i]) d=min(d,G[prevv[i]][preve[i]].cap); f-=d; res+=d*h[t]; //cout<<d<<" "<<h[t]<<" "<<d*h[t]<<endl; for(int i=t; i!=s; i=prevv[i]) { //cout<<i<<" "; edge &e=G[prevv[i]][preve[i]]; e.cap-=d; G[i][e.rev].cap+=d; } //cout<<s<<endl; } return res; } int a[maxn]; int b[maxn]; struct node { int id; int r; double area; }; node cur[maxn]; const double pi = acos(-1.0); int main() { freopen("1.txt","r", stdin); int T; scanf("%d",&T); while(T--) { int n, m; scanf("%d %d", &n, &m); int s = 451; int t = 452; for(int i = 1; i <= n; i++) scanf("%d", &a[i]); for(int i = 1; i <= m; i++) scanf("%d", &b[i]); sort(a + 1, a + n + 1); sort(b + 1, b + m + 1); n = unique(a + 1, a + n + 1) - a - 1; m = unique(b + 1, b + m + 1) - b - 1; double sum = 0; for(int i = 1; i <= n; i++) cur[i].id = 0, cur[i].r = a[i], cur[i].area = (double)cur[i].r * cur[i].r, sum += cur[i].area; for(int i = n + 1; i <= n + m; i++) cur[i].id = 1, cur[i].r = b[i - n], cur[i].area = (double) pi * cur[i].r *cur[i].r, sum += cur[i].area; for(int i = 1; i <= n + m; i++) addedge(s, i, 1, 0), addedge(i, t, 1, 0), addedge(i + 200, t, 1, 0); for(int i = 1; i <= n + m; i++) { for(int j = 1; j <= n + m; j++) { if(i == j) continue; if(cur[i].id == cur[j].id && cur[i].r > cur[j].r) addedge(j, i + 200, 1, -1.0 * cur[j].area); else if(cur[i].id != cur[j].id) { if(cur[i].id) ///圆 { if((double)sqrt(2.0)*cur[i].r - (double)cur[j].r >= eps) { addedge(j, i + 200, 1, -1.0 * cur[j].area); } } else ///矩形 { if(cur[i].r >= 2*cur[j].r) { addedge(j, i + 200, 1, -1.0 * cur[j].area); } } } } } double cost=min_cost_flow(s,t,n+m); printf("%.2f ",(sum + cost)); for(int i=0; i<NN; i++) G[i].clear(); } return 0; }
