先学习一下单调队列与单调栈,其实和STL的也没啥区别,就是手动维护数组。

#include <cstdio> #include <algorithm> using namespace std; const int maxn = 1e6 + 50; struct node { int x, val; }; node q[maxn * 2]; int minv[maxn], maxv[maxn]; int a[maxn]; int n, k; int main() { scanf("%d %d", &n, &k); for(int i = 1; i <= n; i++) scanf("%d", &a[i]); int head = 1, tail = 0; int i = 1; q[++tail].val = a[i], q[tail].x = i; i++; for(; i < k; i++) { while(head <= tail && q[tail].val < a[i]) { tail--; } q[++tail].val = a[i], q[tail].x = i; } if(k == 1) maxv[1] = q[head].val; for(; i <= n; i++) { while(head <= tail && q[tail].val < a[i]) { tail--; } q[++tail].val = a[i], q[tail].x = i; if(q[head].x + k <= i) head++; maxv[i - k + 1] = q[head].val; //printf("%d ", maxv[i - k + 1]); } head = 1, tail = 0; q[++tail].val = a[1], q[tail].x = 1; i = 2; for(; i < k; i++) { while(head <= tail && q[tail].val > a[i]) { tail--; } q[++tail].val = a[i], q[tail].x = i; } if(k == 1) minv[1] = q[head].val; for(; i <= n; i++) { while(head <= tail && q[tail].val > a[i]) { tail--; } q[++tail].val = a[i], q[tail].x = i; if(q[head].x + k <= i) head++; minv[i - k + 1] = q[head].val; } int t = n - k + 1; for(int i = 1; i <= t; i++) { printf("%d", minv[i]); if(i < t) printf(" "); else printf(" "); } for(int i = 1; i <= t; i++) { printf("%d", maxv[i]); if(i < t) printf(" "); else printf(" "); } return 0; } /* 8 1 1 3 -1 -3 5 3 6 7 */

#include <bits/stdc++.h> using namespace std; const int maxn = 1e5 + 50; int q1[maxn * 2], q2[maxn * 2], num[maxn]; int main() { int n, m, k; while(scanf("%d %d %d", &n, &m, &k) != EOF) { for(int i = 1; i <= n; i++) scanf("%d", &num[i]); int he1 = 1, ta1 = 0, he2 = 1, ta2 = 0, ans = 0, cur = 1; for(int i = 1; i <= n; i++) { while(he1 <= ta1 && num[q1[ta1]] < num[i]) ta1--; while(he2 <= ta2 && num[q2[ta2]] > num[i]) ta2--; q1[++ta1] = i, q2[++ta2] = i; while(he1 <= ta1 && he2 <= ta2 && num[q1[he1]] - num[q2[he2]] > k) { if(q1[he1] < q2[he2]) cur = q1[he1++] + 1; else cur = q2[he2++] + 1; } if(he1 <= ta1 && he2 <= ta2 && num[q1[he1]] - num[q2[he2]] >= m) { ans = max(ans, i - cur + 1); } } printf("%d ", ans); } return 0; }
本题和POJ2823很像,只不过是倒着扫,维护一个单调递减的区间。队列内的元素个数就是某个区间的最大值的变化数。
为什么不能正着扫呢? 维护单调递增区间,不好处理那些在最大值后面的小值,把最大值去了,那些也没法加了。 可能有更麻烦的做法。

#include <bits/stdc++.h> using namespace std; const int maxn = 1e7 + 50; typedef long long ll; int n, m, k, p, q, r; ll MOD; int a[maxn]; int qq[maxn]; int main() { int T; scanf("%d", &T); while(T--) { scanf("%d %d %d %d %d %d %lld", &n, &m, &k, &p, &q, &r, &MOD); for(int i = 1; i <= n; i++) { if(i <= k) scanf("%d", &a[i]); else a[i] = ((ll)p * a[i - 1] + (ll)q * i + (ll)r) % MOD; } int head = 1, tail = 0; ll A = 0, B = 0; int i = n; for(; i > n - m + 1; i--) { while(head <= tail && a[qq[tail]] <= a[i]) tail--; qq[++tail] = i; } for(; i >= 1; i--) { while(head <= tail && a[qq[tail]] <= a[i]) tail--; qq[++tail] = i; if(head <= tail && qq[head] >= i + m) head++; A += (ll)a[qq[head]] ^ i; B += (ll)(tail - head + 1) ^ i; // printf("%d %d ", a[qq[head]], (tail - head + 1)); } printf("%lld %lld ", A, B); } return 0; } /* 1 13 6 13 5 5 5 5 13 12 11 10 9 8 7 6 5 4 3 2 1 1 10 1 10 5 5 5 5 3 2 2 1 5 7 6 8 2 9 */
Problem C. Dynamic Graph Matching
$f[i][s]$表示经过前i次操作后,s集合的点已经匹配的方案数。
加边操作,递推公式:$f[i][s]=f[i-1][s]+f[i-1][s-u-v]。$
$f[i-1][s]$表示不使用这条边的情况,$f[i-1][s-u-v]$表示使用这条边的情况,相加就得到添加一条边的情况。
删边操作$f[i][s]=f[i-1][s]-f[i-1][s-u-v]$ 就可以了。

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn = 1111; int f[maxn]; const ll mod = 1e9 + 7; int ans[11]; int main() { int T; scanf("%d", &T); while(T--) { memset(f, 0, sizeof(f)); int n, m; scanf("%d %d", &n, &m); char fu[5]; int u, v; f[0] = 1; for(int i = 1; i <= m; i++) { scanf("%s %d %d",fu, &u, &v); u--, v--; ///从0开始表示点 memset(ans, 0, sizeof(ans)); for(int s = 0; s < (1 << n); s++) { if(((1 << u) & s) && ((1 << v) & s)) { int ccc = 0; if(fu[0] == '+') f[s] = ((ll)f[s] + f[s - (1 << u) - (1 << v)]) % mod; else f[s] = ((ll)f[s] - f[s - (1 << u) - (1 << v)] + mod) % mod; } if(f[s] != 0) { int st = s; int cnt = 0; while(st) { if(st & 1) cnt++; st >>= 1; } ans[cnt / 2] = ((ll)ans[cnt / 2] + f[s]) % mod; } } for(int ge = 1; ge <= (n >> 1); ge++) { printf("%d", ans[ge]); if(ge < (n >> 1)) printf(" "); else printf(" "); } } } return 0; }
Problem G. Interstellar Travel
先学习一发极角排序。
逆时针走起,符合逆时针则 $>0。$

#include <cstdio> #include <algorithm> using namespace std; const int maxn = 100; struct Point { Point(int _x, int _y) { x = _x; y = _y; } Point(){} int x, y; }; Point point[maxn]; Point operator - (Point A, Point B) { return Point(A.x - B.x, A.y - B.y); } int Cross(Point A, Point B) { return (A.x * B.y - A.y * B.x); } bool cmp(Point A, Point B) { int tmp = Cross(A - point[0], B - point[0]); if(tmp > 0) return 1; else if(tmp < 0) return false; } int main() { int cnt = 0; while(~scanf("%d %d", &point[cnt].x, &point[cnt].y)) { cnt++; } sort(point + 1, point + cnt, cmp); for(int i = 0; i < cnt; i++) { printf("(%d,%d) ", point[i].x, point[i].y); } return 0; }
整理个自己的凸包模板。

#include <bits/stdc++.h> using namespace std; const int maxn = 1e3 + 50; const double PI = acos(-1.0); struct Point { Point(int _x, int _y) { x = _x; y = _y; } Point(){} int x, y; }; Point point[maxn]; Point operator - (Point A, Point B) { return Point(A.x - B.x, A.y - B.y); } int Cross(Point A, Point B) { return (A.x * B.y - A.y * B.x); } Point pmin; double dis(Point A, Point B) { return sqrt((double)(A.x - B.x) * (A.x - B.x) + (double)(A.y - B.y) * (A.y - B.y)); } bool cmp(Point A, Point B) { int tmp = Cross(A - point[1], B - point[1]); if(tmp > 0) return 1; else if(tmp == 0 && dis(A , pmin) < dis(B , pmin)) return 1; else return false; } int top = 0; int st[maxn]; void graham(int n) { if(n == 1) { top = 1, st[1] = 1; } else if(n == 2) { top = 2, st[1] = 1, st[2] = 2; } else { for(int i = 1; i <= 2; i++) st[i] = i; top = 2; for(int i = 3; i <= n; i++) { while(top >= 2 && Cross(point[st[top]] - point[st[top - 1]], point[i] - point[st[top - 1]]) <= 0) { top--; } top++; st[top] = i; } } } double f(int x, int y) { return (double)x * x + (double)y * y; } int main() { int T; scanf("%d", &T); while(T--) { int n, L; scanf("%d %d", &n, &L); for(int i = 1; i <= n; i++) scanf("%d %d", &point[i].x, &point[i].y); ///要先找到最下,最左的点作为原点 int k = 1; pmin.x = point[1].x, pmin.y = point[1].y; for(int i = 2; i <= n; i++) { if(pmin.y > point[i].y || (pmin.y == point[i].y && pmin.x > point[i].x)) { pmin.y = point[i].y; pmin.x = point[i].x; k = i; } } point[k] = point[1]; point[1] = pmin; sort(point + 2, point + n + 1, cmp); top = 0; graham(n); double C = 0; for(int i = 1; i < top; i++) { C += (double)sqrt(f(point[st[i]].x - point[st[i+1]].x, point[st[i]].y - point[st[i+1]].y)); // printf("%lf ", C); } C += (double)sqrt(f(point[st[top]].x - point[st[1]].x, point[st[top]].y - point[st[1]].y)); long long ans = 0; C += (double)2.0 * PI * L; printf("%.0lf ",C); if(T!=0) printf(" "); } return 0; }
去重点,去共线。

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn = 2e5 + 50; const double PI = acos(-1.0); struct Point { Point(ll _x, ll _y) { x = _x; y = _y; } Point(){} ll x, y; int id; }; Point point[maxn]; Point operator - (Point A, Point B) { return Point(A.x - B.x, A.y - B.y); } ll Cross(Point A, Point B) { return (A.x * B.y - A.y * B.x); } ll dis(Point A, Point B) { return (A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y); } bool cmp(Point A, Point B) { ll tmp = Cross(A - point[1], B - point[1]); if(tmp < 0LL) return 1; else if(tmp == 0 && dis(A , point[1]) < dis(B , point[1])) return 1; else if(tmp == 0 && dis(A , point[1]) == dis(B , point[1])) { return A.id < B.id; } else return 0; } int top = 0; int st[maxn]; void graham(int n) { if(n == 1) { top = 1, st[1] = 1; } else if(n == 2) { top = 2, st[1] = 1, st[2] = 2; } else { for(int i = 1; i <= 2; i++) st[i] = i; top = 2; for(int i = 3; i <= n; i++) { if(point[i].x == point[st[top]].x && point[i].y == point[st[top]].y) continue; while(top >= 2 && Cross(point[st[top]] - point[st[top - 1]], point[i] - point[st[top - 1]]) >= 0) { if(Cross(point[st[top]] - point[st[top - 1]], point[i] - point[st[top - 1]]) > 0) { top--; } else { if(point[st[top]].id > point[i].id) ///共线,top的点属于线段中间的点,字典序较大,不符 { top--; } else break; } } top++; st[top] = i; } } } int main() { int T; scanf("%d", &T); while(T--) { int n; scanf("%d", &n); for(int i = 1; i <= n; i++) scanf("%lld %lld", &point[i].x, &point[i].y), point[i].id = i; ///要先找到最下,最左的点作为原点 sort(point + 2, point + n + 1, cmp); top = 1; graham(n); for(int i = 1; i <= top; i++) { printf("%d", point[st[i]].id); if(i < top) printf(" "); else printf(" "); } } return 0; } /* 123 7 0 0 3 2 1 1 2 3 3 2 4 0 1 3 */
Aguin的写法真的是天秀。。。。

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn = 2e5 + 10; ll x[maxn], y[maxn], id[maxn], st[maxn]; bool cmp(int i, int j) { if(x[i] != x[j]) return x[i] < x[j]; if(y[i] != y[j]) return y[i] > y[j]; return i < j; } ll cross(int i, int j, int k) { return ((x[i] - x[k]) * (y[j] - y[k]) - (x[j] - x[k]) * (y[i] - y[k])); } vector<ll> can; int main() { int T; scanf("%d", &T); while(T--) { int n; scanf("%d", &n); for(int i = 1; i <= n; i++) { scanf("%lld %lld", &x[i], &y[i]); id[i] = i; } sort(id + 1, id + n + 1, cmp); can.clear(); for(int i = 1; i <= n; i++) ///去掉重点,和x相等,较低的点 { if(i == 1 || x[id[i]] > x[id[i - 1]]) can.push_back(id[i]); } int top = 0; for(int i = 0; i < can.size(); i++) { while(top >= 2 && cross(st[top], can[i], st[top - 1]) > 0) top--; while(top >= 2 && cross(st[top], can[i], st[top - 1]) == 0 && can[i] < st[top]) top--; st[++top] = can[i]; } for(int i = 1; i <= top; i++) printf("%lld%c", st[i], i == top ? ' ' : ' '); } return 0; } /* 123 7 0 0 3 2 1 1 2 3 3 2 4 0 1 3 */
不计复杂度的写法是:
$dp[i][a[i]][a[i-1]][a[i-2]]+=dp[i-1][a[i-1]][a[i-2]][a[i-3]] imes v[gcd(a[i],a[i-1],a[i-2],a[i-3])]$
复杂度应该是$O(m^4n)。$
然后我们发现,在求$gcd(a[i],a[i-1],a[i-2],a[i-3])$的时候,如果$a[i]=2$,那么$a[i-1]=4$或者$6$都已经不重要,因为此时它的$gcd$最大是$2。$
所以我们可以令
$v1=a[i-1];$
$v2=gcd(a[i-1],a[i-2]);$
$v3=gcd(a[i-1],a[i-2],a[i-3]);$
所以$v2$是$v1$的因子,即$v1|v2,v2|v3.$
带入转移方程中:
$dp[i][a[i]][gcd(a[i],v1)][gcd(a[i],v2)]+=dp[i-1][v1][v2][v3] imes v[gcd(a[i], v3)].$
#include <bits/stdc++.h> using namespace std; int main() { int cnt = 0; for(int i = 1; i <= 100; i++) { for(int j = 1; j <= 100; j++) { for(int k = 1; k <= 100; k++) { if(i % j == 0 && j % k == 0) { cnt++; printf("%d %d %d ", i, j, k); } } } } printf("cnt = %d ", cnt); } …… 100 100 5 100 100 10 100 100 20 100 100 25 100 100 50 100 100 100 cnt = 1471
打表出来的状态只有$1471$个。
复杂度$O(nmS).$

#include <bits/stdc++.h> using namespace std; typedef long long ll; const ll mod = 1e9 + 7; ll quick_pow(ll a, ll n) { ll res = 1; while(n) { if(n & 1) res = a * res % mod; n >>= 1; a = a * a % mod; } return res; } int gcd[101][101]; int id[101][101][101], a[101]; struct node { int v1, v2, v3; }st[1500]; int cnt = 0; ll inv[101]; void init() { for(int i = 1; i <= 100; i++) inv[i] = quick_pow(i, mod - 2); for(int i = 1; i <= 100; i++) { for(int j = 1; j <= 100; j++) { gcd[i][j] = __gcd(i, j); } } /// a[i-1] gcd(a[i-1],a[i-2]) gcd(a[i-1],a[i-2],a[i-3]) for(int i = 1; i <= 100; i++) { for(int j = 1; j <= i; j++) { if(i % j != 0) continue; for(int k = 1; k <= j; k++) { if(j % k != 0)continue; st[++cnt] = node{i, j, k}; id[i][j][k] = cnt; } } } } ll v[101], dp[101][1500]; int main() { init(); ///printf("%d ", cnt); 1471 int T; scanf("%d", &T); while(T--) { memset(dp, 0, sizeof(dp)); int n, m; scanf("%d %d", &n, &m); for(int i = 1; i <= n; i++) scanf("%d", a + i); for(int i = 1; i <= m; i++) scanf("%lld", v + i); ///初始化前三个 for(int i = 1; i <= m; i++) { if(a[3] && a[3] != i) continue; for(int j = 1; j <= m; j++) { if(a[2] && a[2] != j) continue; for(int k = 1; k <= m; k++) { if(a[1] && a[1] != k) continue; int v1 = i; int v2 = gcd[v1][j]; int v3 = gcd[v2][k]; int net = id[v1][v2][v3]; dp[3][net]++; // printf("%d %d %d ", v1, v2, v3); } } } for(int i = 3; i < n; i++) ///枚举的是a[i+1] { for(int j = 1; j <= cnt; j++) { if(dp[i][j]) { int v1 = st[j].v1, v2 = st[j].v2, v3 = st[j].v3; for(int k = 1; k <= m; k++) { if(a[i + 1] && a[i + 1] != k) continue; int net = id[k][gcd[k][v1]][gcd[k][v2]]; // printf("%d %d ", i + 1, net); dp[i + 1][net] = (dp[i + 1][net] + dp[i][j] * v[gcd[k][v3]] % mod) % mod; // printf("%d %lld %lld ", gcd[k][v3], v[gcd[k][v3]], dp[i+1][net]); } } } } ll ans = 0; for(int i = 1; i <= cnt; i++) { ans = (ans + dp[n][i]) % mod; } for(int i = 1; i <= n; i++) { if(!a[i]) ans = (ans * inv[m]) % mod; } printf("%lld ", ans); } return 0; } /* 23 4 3 0 0 0 0 3 2 4 */
首先最容易想到的状态是$G[i][j][k]$,表示从$i$到$j$最少经过$k$条路径。
状态转移方程是:$G[i][j][k]=min(G[i][j][k],G[i][p][k-1]+g[p][j])$,表示从$p$到$j$有一条路径。
时间复杂度是$O(n^3 k).$ 肯定超时。
然后就真香系列……
https://blog.csdn.net/qq_34454069/article/details/81292814
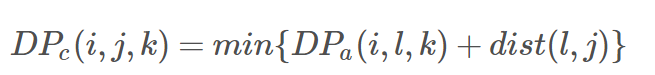
注意此处DPa应该是DPb。
还有个坑点是$DPc[i][j][k]$枚举至少经过$k$条路径的时候,应该从$k=0$开始。因为询问可以是$100$的整数倍。

#include <bits/stdc++.h> using namespace std; int w[55][55]; int dist[55][55]; ///跑一遍Floyd求两点最短路 const int INF = 0x3f3f3f3f; ///k <= 100 int dp0[51][51][101]; ///经过刚好k*100条边 int dp1[51][51][101]; ///刚好经过k条边 int dp2[51][51][101]; ///至少经过k条边的最短路 int main() { // printf("%d ", INF + INF); int T; scanf("%d", &T); while(T--) { int n, m; scanf("%d %d", &n, &m); memset(w, INF, sizeof(w)); memset(dist, INF, sizeof(dist)); memset(dp0, INF, sizeof(dp0)); memset(dp1, INF, sizeof(dp1)); memset(dp2, INF, sizeof(dp2)); for(int i = 1; i <= m; i++) { int u, v, val; scanf("%d %d %d", &u, &v, &val); w[u][v] = min(w[u][v], val); dist[u][v] = w[u][v]; } for(int i = 1; i <= n; i++) { dist[i][i] = 0; dp1[i][i][0] = 0; dp0[i][i][0] = 0; dp2[i][i][0] = 0; } ///Floyd for(int k = 1; k <= n; k++) { for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]); } } } ///刚好经过k条边 for(int k = 1; k <= 100; k++) { for(int l = 1; l <= n; l++) { for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { dp1[i][j][k] = min(dp1[i][j][k], dp1[i][l][k - 1] + w[l][j]); } } } } // printf("%d ", dist[2][2]); ///刚好经过k*100条边 for(int k = 1; k <= 100; k++) { for(int l = 1; l <= n; l++) { for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { dp0[i][j][k] = min(dp0[i][j][k], dp0[i][l][k - 1] + dp1[l][j][100]); } } } } ///至少经过k条边 for(int k = 0; k <= 100; k++) { for(int l = 1; l <= n; l++) { for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { dp2[i][j][k] = min(dp2[i][j][k], dp1[i][l][k] + dist[l][j]); } } } } int q; scanf("%d", &q); while(q--) { int s, t, k; scanf("%d %d %d", &s, &t, &k); int ans = INF; for(int i = 1; i <= n; i++) { ans = min(ans, dp0[s][i][k / 100] + dp2[i][t][k % 100]); } printf("%d ", ans == INF ? -1 : ans); } } return 0; }
