LG3389 「模板」高斯消元法 高斯消元

问题描述

LG3389

---

题解

高斯消元，是用来解(n)元一次方程组的算法，时间复杂度(O(n^3))

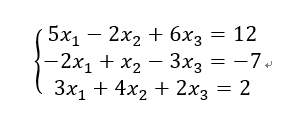
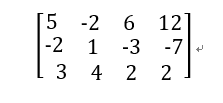
这样就构造出了这个方程组的矩阵

目标就是把这个矩阵左边(n imes n)消为单位矩阵

---

(mathrm{Code})

#include<bits/stdc++.h>
using namespace std;

void read(int &x){
	x=0;char ch=1;int fh;
	while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
	if(ch=='-') fh=-1,ch=getchar();
	else fh=1;
	while(ch>='0'&&ch<='9'){
		x=(x<<1)+(x<<3)+ch-'0';
		ch=getchar();
	}
	x*=fh;
}

#define maxn 107

int n;

double a[maxn][maxn];

int pla;

int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(register int i=1;i<=n;i++){
		for(register int j=1;j<=n+1;j++) cin>>a[i][j];
	}
	for(register int i=1;i<=n;i++){
		pla=i;
		while(pla<=n&&a[pla][i]==0) pla++;
		if(pla==n+1){//如果第i列没有非0的，显然无解
			puts("No Solution");return 0;
		}
		for(register int j=1;j<=n+1;j++) swap(a[i][j],a[pla][j]);//交换到第i行
		double tmp=a[i][i];
		for(register int j=1;j<=n+1;j++) a[i][j]=a[i][j]/tmp;//消除第i行
		for(register int j=1;j<=n;j++){
			if(i==j) continue;
			double rp=a[j][i];
			for(register int k=1;k<=n+1;k++){
				a[j][k]=a[j][k]-rp*a[i][k];//消除其他
			}
		}
	}
	for(register int i=1;i<=n;i++){
		cout<<fixed<<setprecision(2)<<a[i][n+1]<<endl;
	}
	return 0;
}