题目描述
本题中,我们将用符号[c]表示对c向下取整,例如:[3.0」= [3.1」=[3.9」=3。蛐蛐国最近蚯蚓成灾了!隔壁跳
蚤国的跳蚤也拿蚯蚓们没办法,蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。蛐蛐国里现在共有n只蚯蚓(n为正整
数)。每只蚯蚓拥有长度,我们设第i只蚯蚓的长度为a_i(i=1,2,...,n),并保证所有的长度都是非负整数(即:可
能存在长度为0的蚯蚓)。每一秒,神刀手会在所有的蚯蚓中,准确地找到最长的那一只(如有多个则任选一个)
将其切成两半。神刀手切开蚯蚓的位置由常数p(是满足0<p<1的有理数)决定,设这只蚯蚓长度为x,神刀手会将其
切成两只长度分别为[px]和x-[px]的蚯蚓。特殊地,如果这两个数的其中一个等于0,则这个长度为0的蚯蚓也会被
保留。此外,除了刚刚产生的两只新蚯蚓,其余蚯蚓的长度都会增加q(是一个非负整常数)。蛐蛐国王知道这样不
是长久之计,因为蚯蚓不仅会越来越多,还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物,但是
救兵还需要m秒才能到来......(m为非负整数)蛐蛐国王希望知道这m秒内的战况。具体来说,他希望知道:?m秒内
,每一秒被切断的蚯蚓被切断前的长度(有m个数)?m秒后,所有蚯蚓的长度(有n+m个数)。蛐蛐国王当然知道怎
么做啦!但是他想考考你......
输入格式
第一行包含六个整数n,m,q,u,v,t,其中:n,m,q的意义见问题描述;
u,v,t均为正整数;你需要自己计算p=u/v(保证0<u<v)t是输出参数,其含义将会在输出格式中解释。
第二行包含n个非负整数,为ai,a2,...,an,即初始时n只蚯蚓的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。
保证1<=n<=10^5,0<m<7*10^6,0<u<v<10^9,0<=q<=200,1<t<71,0<ai<10^8。
输出格式
第一行输出[m/t]个整数,按时间顺序,依次输出第t秒,第2t秒,第3t秒……被切断蚯蚓(在被切断前)的长度。
第二行输出[(n+m)/t]个整数,输出m秒后蚯蚓的长度;需要按从大到小的顺序
依次输出排名第t,第2t,第3t……的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。即使某一行没有任何数需要 输出,你也应输出一个空行。
请阅读样例来更好地理解这个格式。
输入输出样例

3 7 1 1 3 1 3 3 2

3 4 4 4 5 5 6 6 6 6 5 5 4 4 3 2 2

3 7 1 1 3 2 3 3 2

4 4 5 6 5 4 3 2

3 7 1 1 3 9 3 3 2

//空行 2
说明/提示


【数据范围】
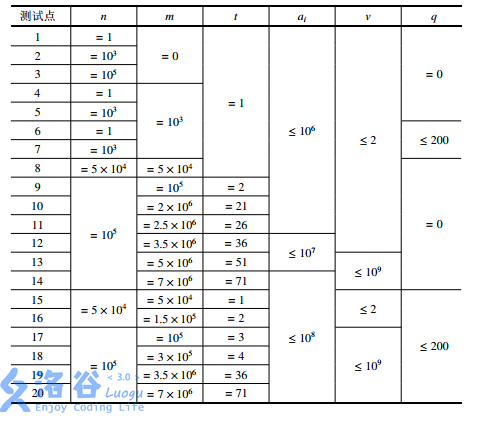
分析
m的最大值已经达到了7e6,这道题我们如果直接枚举的话肯定会超时因为每次都要选出最长的蚯蚓将其切断,所以我们考虑一下它是否具有单调性
我们可以在把所有蚯蚓的长度读入后按照从大到小的顺序排一下序
这样的话,第一次我们肯定会将下标为1的蚯蚓取出将其切断
那么第二次呢?我们还会继续取下标为2的蚯蚓吗,这是不一定的
有可能最长的蚯蚓的长度很长,把它切断后它剩下的部分仍然要比之前长度第2长的蚯蚓要长
那我们可以怎么办呢
当我们切开一条蚯蚓时,必定会把它分成两部分
我们可以把其中较大的一个部分扔到一个大根堆中,再把其中较小的部分扔到另一个大根堆中
这样,我们每次在原数组和这两个大根堆中取一个最大值
把这个最大值作为切开的蚯蚓,按照上面的操作把切开的两部分分别扔到两个堆中
那么每次操作后蚯蚓的长度都会增加一个值q,这该怎么处理呢
把每个数都枚举一遍分别加上q显然是不现实的
我们可以开一个变量ad记录到当前的时间蚯蚓长度的增加量
比如过了1秒,ad=q,过了2秒,ad=2q……过了n秒,ad=nq
每次取出一个元素把它加上ad就可以了
但这时又有一个问题,被切断的蚯蚓在那一秒内长度是不会变化的,如果我们还给它加上ad,显然会出错
所以我们在把它放到堆中时,先将它的值减去ad
大家可以这样理解,这条蚯蚓是在第m秒生成的,
也就是说,在前m秒,它的长度并不会增加
这样如果没有任何处理的话,它的长度会多算在它被切割那一秒时的ad值,所以我们再把它放进堆中时,要把它的长度减去那一秒时的ad值
这样的话,我们就可以写出如下的代码

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<iostream> 5 #include<queue> 6 using namespace std; 7 typedef long long ll; 8 const int maxn=8000000+5; 9 ll a[maxn]; 10 bool cmp(ll aa,ll bb){ return aa>bb; } 11 priority_queue<ll> qq,xi,da; 12 int main(){ 13 ll n,m,q,u,v,t; 14 scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&q,&u,&v,&t); 15 for(ll i=1;i<=n;i++){ 16 scanf("%lld",&a[i]); 17 } 18 sort(a+1,a+1+n,cmp); 19 ll head=1,tail=n; 20 ll js=0,ad=0; 21 while(m--){ 22 js++; 23 ll ans=-0x3f3f3f3f3f3f3f3f; 24 ll bb=ans,cc=ans,dd=ans; 25 if(!xi.empty()) bb=xi.top(); 26 if(!da.empty()) cc=da.top(); 27 if(head<=tail) dd=a[head]; 28 ans=max(max(ans,bb),max(cc,dd)); 29 if(ans==bb) xi.pop(); 30 else if(ans==cc) da.pop(); 31 else head++; 32 ans+=ad; 33 if(js%t==0) printf("%lld ",ans); 34 ad=js*q; 35 ll left=u*ans/v; 36 ll right=ans-left; 37 left-=ad,right-=ad; 38 xi.push(min(left,right)); 39 da.push(max(left,right)); 40 } 41 printf(" "); 42 for(ll i=head;i<=tail;i++) {qq.push(a[i]);} 43 while(!xi.empty()) {qq.push(xi.top()),xi.pop();} 44 while(!da.empty()) {qq.push(da.top()),da.pop();} 45 ll cnt=0; 46 while(!qq.empty()){ 47 cnt++; 48 if(cnt%t==0) printf("%lld ",qq.top()+ad); 49 qq.pop(); 50 } 51 printf(" "); 52 return 0; 53 }
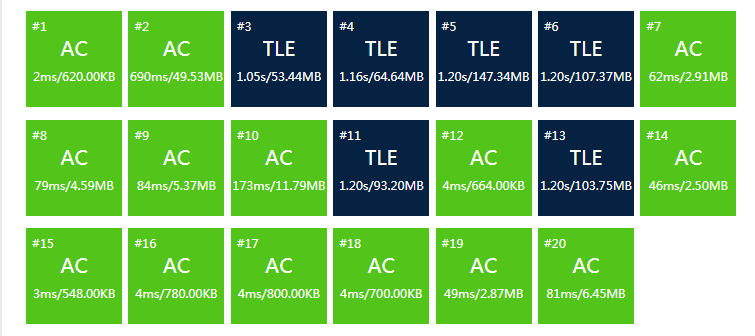
这样写T掉是必然的,因为你用优先队列的话,每次插入时间复杂度都为O(logn)
这样的效率肯定会有数据T掉
那么我们再仔细想想,发现其实是没有必要用优先队列的
因为我们每一次都是先把最长的蚯蚓切割,所以先切的蚯蚓一定长于后切的蚯蚓
所以先切的蚯蚓的较长的部分一定长于后切的蚯蚓较长的部分,所以先切的蚯蚓的较短的部分一定长于后切的蚯蚓较短的部分
所以用来储存切割后两部分的两个堆都具有单调性,因此我们可以用数组模拟,这样会快很多

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<iostream> 5 #include<queue> 6 using namespace std; 7 #define maxn 7000005 8 #define ll long long 9 ll a[maxn],xi[maxn],da[maxn]; 10 bool cmp(ll aa,ll bb){ return aa>bb; } 11 int main(){ 12 ll n,m,q,u,v,t; 13 scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&q,&u,&v,&t); 14 for(register ll i=1;i<=n;++i){ 15 scanf("%lld",&a[i]); 16 } 17 sort(a+1,a+1+n,cmp); 18 ll ha=1,ta=n,hx=1,hd=1,tx=0,td=0; 19 ll js=0,ad=0; 20 ll mm=m; 21 while(mm--){ 22 js++; 23 ll ans=-0x3f3f3f3f3f3f3f3f; 24 if(ha<=ta && a[ha]>=ans) ans=a[ha]; 25 if(hx<=tx && xi[hx]>=ans) ans=xi[hx]; 26 if(hd<=td && da[hd]>=ans) ans=da[hd]; 27 if(a[ha]==ans && ha<=ta) ha++; 28 else if(xi[hx]==ans && hx<=tx) hx++; 29 else hd++; 30 ans+=ad; 31 if(js%t==0) printf("%lld ",ans); 32 ll left=u*ans/v; 33 ll right=ans-left; 34 ad=js*q; 35 left-=ad,right-=ad; 36 xi[++tx]=min(left,right); 37 da[++td]=max(left,right); 38 } 39 printf(" "); 40 ll now=n+m; 41 for(ll i=1;i<=now;++i){ 42 ll ans=-0x3f3f3f3f3f3f3f3f; 43 if(ha<=ta && a[ha]>=ans) ans=a[ha]; 44 if(hx<=tx && xi[hx]>=ans) ans=xi[hx]; 45 if(hd<=td && da[hd]>=ans) ans=da[hd]; 46 if(a[ha]==ans && ha<=ta) ha++; 47 else if(xi[hx]==ans && hx<=tx) hx++; 48 else hd++; 49 if(i%t==0) printf("%lld ",ans+ad); 50 } 51 printf(" "); 52 return 0; 53 }

这样的话,我们交到洛谷上可以过,但是在Vjudge上会T掉
于是,我又加上了读入优化、输出优化,以及register、inline等等,但发现还是会T

就像上面这样
后来我发现,其实没有必要写额外的读入优化、输出优化
一开始,我为了不炸int,把所有的变量都开成了long long
但实际上,有很多变量只用int就能解决,而且int比long long要快
只要把不必要的long long改成int就可以AC了

代码

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<iostream> 5 #include<queue> 6 using namespace std; 7 #define maxn 7000005 8 #define ll long long 9 int a[maxn]; 10 ll xi[maxn],da[maxn]; 11 int cmp(int aa,int bb){ return aa>bb; } 12 int main(){ 13 int n,m,q,u,v,t; 14 scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t); 15 for(int i=1;i<=n;++i){ 16 scanf("%d",&a[i]); 17 } 18 sort(a+1,a+1+n,cmp); 19 int ha=1,ta=n,hx=1,hd=1,tx=0,td=0; 20 ll js=0,ad=0; 21 int mm=m; 22 while(mm--){ 23 js++; 24 ll ans=-0x3f3f3f3f3f3f3f3f; 25 if(ha<=ta && a[ha]>=ans) ans=a[ha]; 26 if(hx<=tx && xi[hx]>=ans) ans=xi[hx]; 27 if(hd<=td && da[hd]>=ans) ans=da[hd]; 28 if(a[ha]==ans && ha<=ta) ha++; 29 else if(xi[hx]==ans && hx<=tx) hx++; 30 else hd++; 31 ans+=ad; 32 if(js%t==0) printf("%lld ",ans); 33 ll left=u*ans/v; 34 ll right=ans-left; 35 ad=js*q; 36 left-=ad,right-=ad; 37 xi[++tx]=min(left,right); 38 da[++td]=max(left,right); 39 } 40 printf(" "); 41 int now=n+m; 42 for(int i=1;i<=now;++i){ 43 ll ans=-0x3f3f3f3f3f3f3f3f; 44 if(ha<=ta && a[ha]>=ans) ans=a[ha]; 45 if(hx<=tx && xi[hx]>=ans) ans=xi[hx]; 46 if(hd<=td && da[hd]>=ans) ans=da[hd]; 47 if(a[ha]==ans && ha<=ta) ha++; 48 else if(xi[hx]==ans && hx<=tx) hx++; 49 else hd++; 50 if(i%t==0) printf("%lld ",ans+ad); 51 } 52 printf(" "); 53 return 0; 54 }
