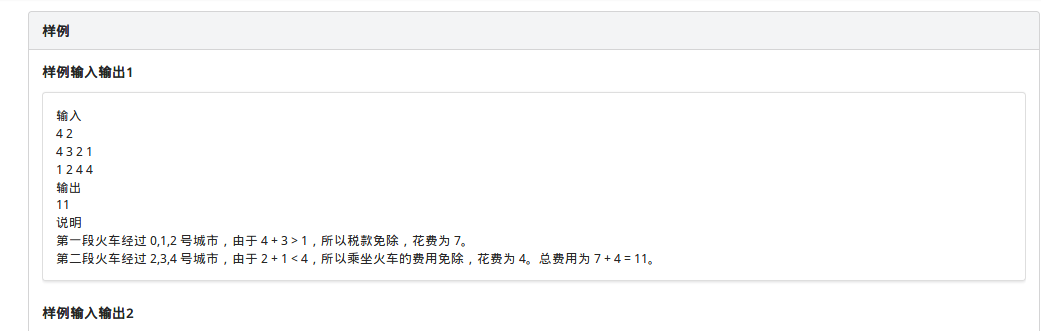
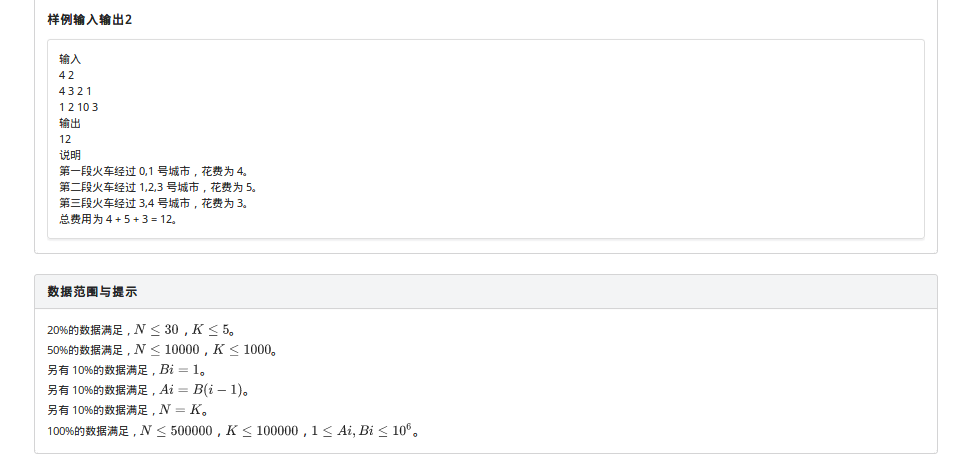
题目描述
分析
(50) 分的 (n^2DP) 比较好想
设 (f[i]) 为在 (i) 处下车的最小花费,(sum[i]) 为 (a[i]) 的前缀和
则 (f[i]=min(f[i],f[j]+max(b[j],s[i]-s[j])))
考虑如何优化

代码
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<iostream>
#include<queue>
#include<vector>
inline int read(){
int x=0,fh=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=5e5+5;
typedef long long ll;
int n,m,a[maxn],b[maxn];
ll f[maxn],sum[maxn];
struct asd{
int id;
ll val;
asd(){}
asd(int aa,ll bb){
id=aa,val=bb;
}
bool operator < (const asd &A) const{
return val>A.val;
}
};
std::priority_queue<asd> q1;
std::priority_queue<asd> q2;
int main(){
freopen("empire.in","r",stdin);
freopen("empire.out","w",stdout);
memset(f,0x3f,sizeof(f));
n=read(),m=read();
for(int i=1;i<=n;i++){
a[i]=read();
}
for(int i=1;i<=n;i++){
b[i-1]=read();
}
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+a[i];
}
f[0]=0;
ll nans;
for(int i=1;i<=n;i++){
q1.push(asd(i-1,f[i-1]+b[i-1]));
nans=0x3f3f3f3f3f3f3f3f;
while(!q1.empty() && i-q1.top().id>m) q1.pop();
while(!q2.empty() && i-q2.top().id>m) q2.pop();
while(!q1.empty()){
int now=q1.top().id;
if(q1.top().val<=f[now]-sum[now]+sum[i]){
q2.push(asd(now,f[now]-sum[now]));
q1.pop();
} else {
break;
}
}
while(!q1.empty() && i-q1.top().id>m) q1.pop();
while(!q2.empty() && i-q2.top().id>m) q2.pop();
if(!q1.empty()) nans=std::min(nans,q1.top().val);
if(!q2.empty()) nans=std::min(nans,q2.top().val+sum[i]);
f[i]=nans;
}
printf("%lld
",f[n]);
return 0;
}