# 递归的三个条件 # 基本结束条件 # 向基本结束条件演进 # 调用自身
# 理解递归
# 递归就是把大问题一步步不断的化解为小问题,小问题解决后在一步步依赖回去解决大问题。
# (1+3+5+7+9)
# -> (1+(3+5+7+9))
# ->(1+(3+(5+7+9)))
# ->(1+(3+(5+(7+9))))
# ->(1+(3+(5+(7+(9))))
# (1+(3+(5+(7+(9)))) # if len(num_list)== 1
# (1+(3+(5+(16))))<-
# (1+(3+(21)))<-
# (1+(24))<-
# (25)<-
# 迭代与递归求和对比 def list_sum1(num_list): result = 0 for i in num_list: result += i return result def list_sum2(num_list): if len(num_list) == 1: return num_list[0] else: return num_list[0] + list_sum2(num_list[1:]) # 四种求阶乘
# 迭代 reduce+lambda math 递归 def fact1(num): while num is not None: if num < 0: return False elif num == 0: return 1 else: count = 1 for i in range(1, num+1): count *= i return count from functools import reduce def fact2(num): while num is not None: if num < 0: return False elif num == 0: return 1 else: return reduce(lambda x,y:x*y,range(1,num+1)) def fact3(num): import math while num is not None: return math.factorial(num) def fact4(num): if num == 0: return 1 else: return num * fact4(num-1) print(fact4(5)) # 递归的实例 # int 转 str 整数转任意进制的字符串 # 基本结束条件 直到 n/base 整除后的n值小于进制数 # 向基本结束条件演进 每当 n/base <= base 时都进一个取余完的字符串 # 调用自身 每次 n 变成 n/base def int_to_str(n, base): convert_string = '0123456789ABCDEF' if n < base: return convert_string[int(n)] else: return int_to_str(n/base, base)+convert_string[int(n%base)] print(int_to_str(1453, 16)) # 字符串逆序 # 结束 字符串为空 # 演进 每调用一次,开头的字符就加到后面一次,字符串就少头部一个 # 调用 调用自身,将每次的字符串分为 开头第一个字符在最后,余下的在前面 def reverse_str(aString): if aString == '': return aString else: return reverse_str(aString[1:])+aString[0] print(reverse_str('hello')) # 判断回文词 def palchecker(aString): import string aString = aString.translate(str.maketrans('','', string.punctuation)).replace(' ','') print(aString) if len(aString) < 2: return True elif aString[0] != aString[-1]: return False return palchecker(aString[1:-1]) print(palchecker('radm i,m dar')) # 递归的内部实现 栈帧 fp sp # python默认深度998 最大深度3800 sys.setrecursionlimit() # print(fact4(1000)) RecursionError: maximum recursion depth exceeded in comparison # 栈帧空间就是运行函数的, # 调用函数就是开辟一个新的栈帧空间, # 调用结束后会自动释放栈帧空间
# 函数调用过程
# 去的过程: # 没调用一个函数就开辟一块新的栈帧空间, # 每结束一个变量, 就释放一个栈帧空间 # 递归本质上就是开辟和释放栈帧空间的过程 # 回的过程: 需要触底反弹 # 1.当前这层栈帧空间的代码全部执行完毕, # 会自动回到上一层函数的调用处 # 2.当前函数遇到return会终止当前函数 # 回到上一层函数的调用处 def digui(n): print(n) if n > 0: digui(n-1) print(n) digui(5) # 代码从上到下执行: # digui(5) # print 5 # digui(4) # print 4 # digui(3) # print 3 # digui(2) # print 2 # digui(1) # print 1 # digui(0) # print 0 # n !> 0 # print 0 # 最内层的函数已经结束 # 开始向外面跳转 # print 1 # print 2 # print 3 # print4 # prin 5
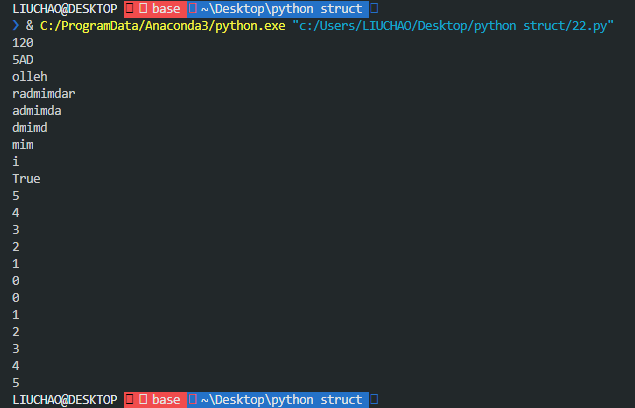
运行情况: