HDU-2067-小兔的棋盘

转载自 ______________白白の屋

题目链接

http://acm.hdu.edu.cn/showproblem.php?pid=2067

这个题目，题意都没有弄明白，有点难度啊！这个题目是个好题。

看了大牛的结题报告：

题目分析:

假设小兔的棋盘是 8 × 8 的 ( 当然你也可以假设是其他 )。如下图:
箭头方向表示从该格子下一步能去的格子。因为不能穿越对角线，所有对角线上的格子只有进去的箭头，没有出来的箭头。

 

这图画的太好了。
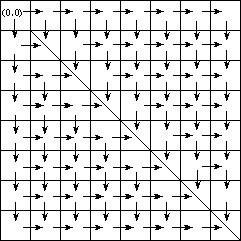
观察上图你就可以发现，其实这是一张关于对角线对称的图。所有我们只要求一个方向的值，然后乘以2即可。
我们就拿下三角来考虑。不难发现，所有在0列上的格子，路径数都是 1 (只能从上面过来)。
而其他格子则都是由上、左两个方向过来，即:f(i, j) = f(i - 1, j) + f(i, j - 1);
另外f(i, i) = f(i, j - 1)  或者 f(i, i) = f( i-1, j ) ;

代码如下:

#include<iostream>
using namespace std;
typedef long long int64;
int64 f[37][37];
int main()
{
    int ca=0;
    int N;
    while ( cin >> N , N + 1 )
    {
        ++ ca;
        for ( int i = 1;i <= N; ++ i )
        {
              f[0][i] = 1;
        }
        for ( int i = 1; i < N; ++ i )
        {
              for ( int j = i; j <= N; ++ j )
              {
                    if ( i == j )
                    {
                         f[i][j] = f[i-1][j];
                    }
                    else
                    {
                         f[i][j] = f[i-1][j] + f[i][j-1];
                    }
              }
        }
        printf("%d %d %I64d ", ca, N, 2 * f[N-1][N] );
    }
    return 0;
}

另外看别人的解题报告说这个是卡特兰数 ( 详细请查看 <<卡特兰数>>  ), 其实现在还不理解, 分析如下:

Catalan数。。
令h(1)＝1,h(0)=1，catalan数满足递归式：
　　h(n)= h(0)*h(n-1)+h(1)*h(n-2) +  + h(n-1)h(0) (其中n>=2)
　　另类递归式：
　　h(n)=((4*n-2)/(n+1))*h(n-1);
　　该递推关系的解为：
　　h(n)=C(2n,n)/(n+1) (n=1,2,3,…)

附卡特兰代码:

#include<stdio.h>
int main()
{
    __int64 a[37][37]={0};
    int i,j,n,t=0;
    a[0][0]=0;
    a[0][1]=1;
    a[1][1]=2;
    for(i=2;i<37;i++)
    {
        a[i][0]=1;
        for(j=1;j<i-1;j++)
            a[i][j]=a[i][j-1]+a[i-1][j];
        a[i][i-1]=a[i][i-2]+a[i-1][i-1]/2;
        a[i][i]=2*a[i][i-2]+a[i-1][i-1];
 
    }
    while(scanf("%d",&n)&&n!=-1)
    {
        printf("%d %d %I64d ",++t,n,a[n][n]);
    }
    return 0;
}

我的代码

#include<stdio.h>
#include<string.h>

__int64 a[40];

int main(void)
{
__int64 i,j,k,n;
a[1]=1;
for(i=2;i<=35;i++)
a[i]=(4*i-2)*1.0/(i+1)*a[i-1];
k=1;
while(scanf("%I64d",&n)==1&&n!=-1)
{
printf("%I64d %I64d %I64d ",k++,n,a[n]*2);
}
return 0;
}

这里有一个细节必须说一下       有  a*b/c   且a，b，c 是整数。   如果a*b很大数据漏出的话，改变成a/c*b是不行的  在于当 a%c！=0 时是不行的

可以这样处理   a*1.0/c*b  这样就可行了。

    

代码

#include<stdio.h>

int main(void)
{
__int64 dp[36][36];
int i,j,k=1,n;
while(scanf("%d",&n)==1&&n!=-1)
{
for(i=1;i<=n;i++)
dp[0][i]=1;
for(i=1;i<n;i++)
{
for(j=i;j<=n;j++)
{
if(i==j)
{
dp[i][j]=dp[i-1][j];
}
else
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
}
printf("%d %d %I64d ",k++,n,2*dp[n-1][n]);
}
return 0;
}