使用条件
优化函数在搜索区间内为单峰函数
算法
算法类似于二分查找算法,能够求单峰函数在搜索区间的极值
算法如下:
(step0:)
(qquad)确定单峰函数(f(x))的搜索区间([a_0,b_0]);容错误差(delta=a-b), (epsilon=f(b)-f(a)) ,t=0.618;(p=a_0+(1-t)(b_0-a_0)),(q=a_0+t(b_0-a_0))
(step1:)
[f(p) <=f(q)egin{cases} yes, & ext{to step 2}\ no, & ext{to step 3} end{cases}
]
(step2:)
if |f(b)-f(a)| >= $epsilon or |b-a|>=delta$
b=q,f(b)=f(q), q=p, f(q)=f(p);
p=a+(1-t)(b-a), resolve f(p);
else
stop;
print p;\p为求得极值点
(step3:)
if |f(b)-f(a)| >= $epsilon or |b-a|>delta$
a=p,f(a)=f(p), p=q, f(p)=f(q);
q=a+t(b-a), resolve f(q);
else
stop;
print q;\p为求得极值点
算法实现函数:
function [R,loos,loos_t] = xiansousuo_golds(func,a,b,delta,epsilon,iterate)
t = (sqrt(5)-1)/2;
p = a+(1-t)*(b-a);
q = a+t*(b-a);
f_a=func(a);
f_b=func(b);
f_p = func(p);
f_q = func(q);
R=zeros(1,2);
loos_t = zeros(iterate,1);
loos = zeros(1,2);
%step1
k=0;
while abs(f_b-f_a)>=epsilon || abs(b-a) >= delta || k < iterate
k=k+1;
loos_t(k,1)=abs(f_b-f_a);
if f_p <= f_q
b=q;
f_b=f_q;
q=p;
f_q =f_p;
p=a+(1-t)*(b-a);
f_p = func(p);
else
a=p;
f_a=f_p;
p=q;
f_p =f_q;
q=a+t*(b-a);
f_q=func(q);
end
%disp([p,abs(f_b-f_a)]);
end
if f_p <= f_q
R(1,1)=p;
R(1,2)=func(p);
else
R(1,1)=q;
R(1,2)=func(q);
end
loos=[abs(b-a),abs(f_b-f_a)];
end
main函数
clc;
close all;
iterate=30;
func=@(s) s^2-sin(s);
[R,loos,loos_t]=xiansousuo_golds(func,0,1,1e-4,1e-5,iterate);
disp(R);
disp(loos);
figure(1);
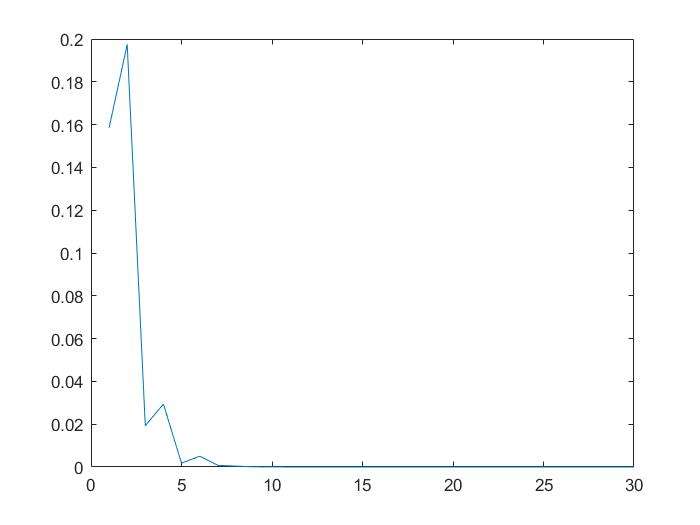
plot(1:iterate,loos_t);
figure(2);
t=linspace(0,1,iterate);
y=zeros(iterate,1);
for i =1:iterate
y(i,1)=func(t(i));
end
plot(t,y);
hold on;
minimum = fminbnd(func,0,1);
f_min=func(minimum);
plot(minimum,f_min,'rp','MarkerSize',10);
text(minimum,f_min,['(',num2str(minimum),',',num2str(f_min),')'],'color','b');
disp([minimum,f_min]);
epsilon随迭代变化
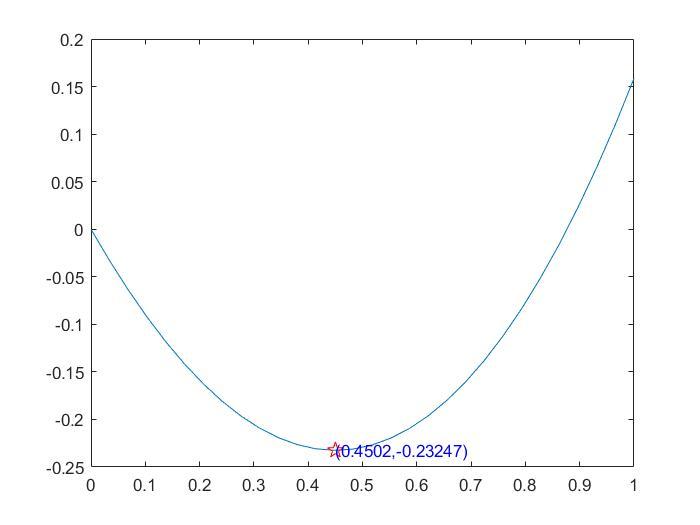
所求函数及极小值
conclusion
- 算法求得结果和matlab极小值函数结果相同,精度较高;
- 对于应用范围有限制【单峰函数】。