牛顿算法及其改进【阻尼牛顿法、修正牛顿法】

牛顿算法

对于优化函数(f(x)),(x=(x_1;x_2;...;x_n)),二阶连续可导

在(x_k)处泰勒展开，取前三项，即对于优化函数二阶拟合

[f(x)=f(x_k)+g_k(x-x_k)+frac{1}{2}(x-x_k)G_k(x-x_k) ]

其中(g_k= abla f(x_k)),为函数梯度；(G_k= abla^2f(x_k))，为函数的Hesse矩阵
当(G_k)正定时，上式存在极小值，使得( abla f(x)=0)

( abla f(x)=g_k+G_k(x-x_k)=0)
可得牛顿法迭代公式：

[x_{k+1}=x_k-G_k^{-1}g_k ]

1. 可见，对于牛顿法，需要计算二阶偏导数（Hesse矩阵），且Hesse矩阵必须可逆、正定
2. 并且，牛顿法对于迭代初始值(x_0)也有要求，当(x_0)距离最优解(x*)足够近时，算法才收敛

阻尼牛顿法

阻尼牛顿法解决了第二个问题，使得算法全局收敛
主要方法是引入线搜索技术，使得算法满足收敛性条件，关于线搜索技术
线搜索

算法：

(step0:)
给定迭代初始值(x_0),和容许误差(epsilon)

(step1:)
计算梯度(g_k= abla f(x_k))
if (||g_k||<epsilon),break；输出当前(x_k)
else 解方程：

[G_kd_k=-g_k ]

求出迭代方向$d_k$, to step 2

(step2:)
利用Armijo准则算法，计算迭代步长(alpha_k)

[x_{k+1}=x_k+alpha_k d_k ]

k=k+1;to step 1

修正的牛顿算法

上面算法有前提条件1（Hesse矩阵正定）
为了扩大算法的适用范围，对算法修正，解决条件1 的强制条件，有两种方法

方法1：

对于阻尼牛顿算法求得的迭代方向(d_k),检查是否满足收敛条件：

[g_k^Td_k<0 ]

if 满足
(d_k=d_k)
else
(d_k=-g_k)

就是牛顿算法和梯度下降算法的混合算法，当牛顿算法求得迭代方向不满足收敛条件，使用负梯度方向为迭代方向

关于为什么不直接使用梯度下降法

可以证明：牛顿算法是二阶收敛，梯度下降线性收敛【牛顿法收敛速度快】

方法2

引进阻尼因子(mu_k),对Hesse矩阵修正,选择适当(mu_k),使得

[G_k=G_k+mu_kI ]

正定

方法二matlab代码

function [x,val,fun_t] = revise_newton(fun,gfun,hesse,x0,iterate)
%revise_newton - Description
%
% Syntax: [x,val,fun_t] = revise_newton(fun,gfun,hesse,x0)
%
% 修正牛顿法

    n=length(x0);maxk=iterate;
    rho=0.55;Sigma=0.4;tau=0.0;
    k=0;epsilon=1e-5;
    fun_t=zeros(1,maxk);
    while k<maxk

        k=k+1;
        fun_t(1,k)=fun(x0);

        gk=gfun(x0);
        muk=norm(gk)^(1+tau);
        Gk=hesse(x0);
        Ak=Gk+muk*eye(n);
        dk=-Akgk;
        if norm(gk)<epsilon
            break;
        end
        m=0;mk=0;
        while m<20
            if fun(x0+rho^m*dk)<fun(x0)+Sigma*rho^m*gk'*dk
                mk=m;
                break;
            end
            m=m+1;
        end
        x0=x0+rho^mk*dk;
    end

    x=x0;
    val=fun(x);
end

main functin

clc;
close all;

fun=@(x) 100*(x(1)^2-x(2))^2+(x(1)-1)^2;
gfun=@(x) [400*(x(1)^2-x(2))*x(1)+2*(x(1)-1);-200*(x(1)^2-x(2))];
hesse=@(x) [1200*x(1)^2-400*x(2)+2,-400*x(1);-400*x(1),200];

x0=[0;0];
iterate=30;

[x,val,fun_t] = revise_newton(fun,gfun,hesse,x0,iterate);

disp(x);
disp(val);
figure(1);
plot(1:iterate,fun_t);
set(get(gca, 'XLabel'), 'String', 'number of iterations');
set(get(gca, 'YLabel'), 'String', 'function value');

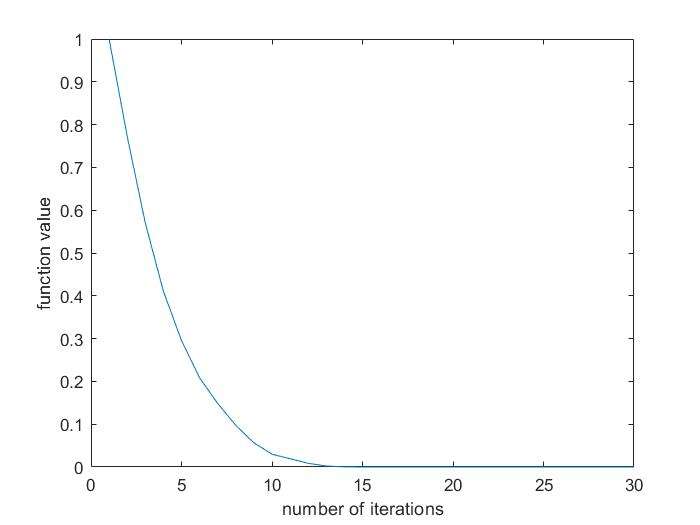
result

conclusion

上述图像为函数值随迭代次数变化，可见收敛速度较快；且计算结果较精确；

reference

《最优化方法及其matlab程序设计》