深度滤波器(2)——三角化深度值的误差分析

上一篇文章中，我们介绍了单目SLAM中的三角化恢复三维点深度的原理，本篇文章我们来聊一聊三角化深度值的误差分析。

目录：

(1)三角化所带来的误差的提出

(2)三角化中误差的来源分析

(3)如何减小三角化所带来的误差

(4)三角化所遇到的奇异情况

---

(1)三角化所带来的误差的提出

上一篇文章中，我们提到了两帧图像中的特征点坐标三角化得到空间点的三维信息。

今天，我们来分析一下三角化得到的三维信息中深度的误差。

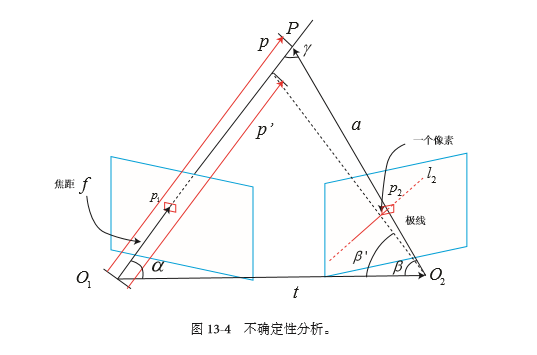
如上图所示：

P为空间中的一个三维点，p₁和p₂分别为在两个位置处，摄像机观察到的投影的二维点坐标。

l₂为p₁在第二幅图中所对应的极线（极线的概念请参考立体视觉中的对极几何，这里不再赘述）。

现在，我们要探讨的是：

如果我们在l₂进行极线搜索时，所找到的p_2^'点与真实的p₂点有一个像素的误差，那么会给三角化后的三维点P的深度z带来多大的误差。

首先，根据上图，我们可以得到向量之间的关系，以及三角化中的两个夹角的定义：

a = p - t                公式(1)

α = arccos<p, t>    公式(2)

β = arccos<a, -t>   公式(3)

其中，a, p, t均为向量，α和β为图中所示的两个夹角。

如果此时，我们求取的p_2^'点与p₂点有一个像素的偏差，同时，这一个像素的偏差又会给β带来δβ的角度变化，我们利用β'来表示对β进行δβ扰动后的新的角度。

设相机的焦距为f，则：

公式(4):

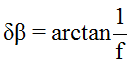
公式(5):

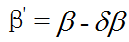
公式(6):

至此，加入扰动后的所有新的角度我们都求出来了。

由正弦定理，我们可以得到：

公式(7):

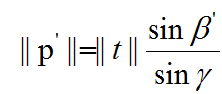
则由第二个位置上的二维点的一个像素的误差，可能导致的三角化后深度的误差为：

 δp = ||p|| - ||p'||

 这里的δp其实也正是深度的一个均方差（不确定度σ_obs），这个不确定度是我们后面要介绍的深度滤波器的一个很重要的概念，深度滤波器的目的也正是要不断减小这个不确定度，使得深度的不确定度最后能够收敛到一个能够接受的值。

(2)三角化中误差的来源分析

上面分析了第二幅图中的特征点p₂的误差是如何影响三角化后的深度值的。 

下面，我们来指出三角化的误差来源有哪几方面：

a.图像的分辨率：图像的分辨率越高，一个像素所带来的δβ就越小。

b.特征点求取时的精度：是否做到亚像素，在亚像素的基础上，误差有多大？

c.p₁点的误差：会引起极线l₂的误差，从而间接地影响p₂点的精度。

d.相机两次位置的平移向量t的大小：t的模的大小也代表了对极几何中的基线长度，由公式(7)可以看出基线长度越大，三角化的误差越小。

(3)如何减小三角化所带来的误差

根据【(2)三角化中误差的来源分析】中所分析的一些因素可知，要想减小三角化过程中引入的误差，可以有如下几个方法：

a.选取尽可能高分辨率的相机。

b.进行亚像素的优化（比如在极线搜索时对像素点坐标进行双线性插值）

// 双线性灰度插值 
inline double getBilinearInterpolatedValue( const Mat& img, const Vector2d& pt ) 
{
    uchar* d = & img.data[ int(pt(1,0))*img.step+int(pt(0,0)) ];
    double xx = pt(0,0) - floor(pt(0,0)); 
    double yy = pt(1,0) - floor(pt(1,0));
    return  (( 1-xx ) * ( 1-yy ) * double(d[0]) +
            xx* ( 1-yy ) * double(d[1]) +
            ( 1-xx ) *yy* double(d[img.step]) +
            xx*yy*double(d[img.step+1]))/255.0;
}

（关于双线性插值，这篇文章做了比较清晰的讲解：http://blog.163.com/guohuanhuan_cool@126/blog/static/167614238201161525538402/）

c.同样使用亚像素级的图像处理算法来处理p₁点。

d.在不丢失特征点的情况下，让平移量t尽量大。

(4)三角化所遇到的奇异情况

由上面的公式推导我们可以看出，三角化中，必须要有平移量t，否则无法构成三角形，进行三角化。

所以在有些单目的SLAM，AR/VR的场景中，有经验的人都会有意识地将设备或者相机进行一定量的平移，而不会在原地进行纯旋转。

总结一下，我们今天分析了三角化过程中的误差有哪些，并从理论上对误差进行了量化的推导。同时，我们还分析了如果减小三角化过程中的误差。

下一篇文章，我们将会带着大家一起分析深度滤波器的原理。敬请期待！