深度滤波器(3)——深度滤波器的原理及实现

在前两篇文章中，我们介绍了三角化恢复深度信息，并对三角化过程中的误差进行了分析和讨论。

今天，我们就进入我们这个系列的正题：深度滤波器的原理及实现。

一提到深度滤波器，大家肯定首先会觉得深不可测，听名字就觉得高大上。其实，有了前面的预备知识，不难理解今天要讲解的深度滤波器的原理。

我们今天给大家介绍的是比较简单的高斯分布假设下的深度滤波器。

高斯分布是自然界中最常见的一种分布形式，并且也符合绝大部分的自然情况。简单起见，我们先假设三角化后恢复的深度值符合高斯分布。对于像素点的深度值d，满足：

P(d) = N(μ，σ²)

每当新的数据过来，我们就要利用新的观测数据更新原有的深度d的分布。

这里的数据融合的方式与经典的Kalman滤波方式大同小异。

这里，我们利用观测方程进行信息融合。

假设新计算出来的深度数据的分布为：

P(d_obs) = N(μ_obs，σ_obs²)

我们将新计算出来的深度数据乘在原来的分布上，进行信息融合的更新：

我们知道，利用两个高斯分布的乘积的分布公式，可以得到融合后的高斯分布：

P(d_fuse) = N(μ_fuse, σ_fuse²)

其中，

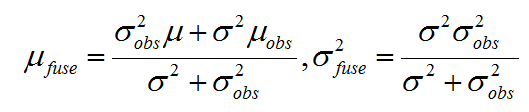
那么问题来了，这里的μ_obs，σ_obs²该如何才能得到呢？

这里的μ_obs实际上就是每次我们新三角化出来的深度值，而对于σ_obs²，如果你还对上一篇文章有印象的话，就会记得我们推导了一系列公式所得到的那个 δp（不确定度σ_obs），如果你忘记了，可以回去上一篇文章再复习一下。

那么原始的分布μ，σ²该如何得到呢？

这个很简单，第一次三角化出来的μ，σ²就可以作为初始值，然后每次新三角化出一个三维点，就去更新深度值的分布。

至此，我们似乎得到了一个不错的结果：既简单又优美的公式。

实际上还会存在什么问题呢？

（1）实际的深度值分布是否真的符合高斯分布？

（2）如果我们中间过程有一次三角化的过程求错了，并且还进行了信息融合，会有什么后果？

（3）我们如何避免第二个问题中所提出的情况？

这些问题留给读者去思考，也欢迎在下方给我留言，一起探讨这些问题的解决方案。

下篇文章我将会带着大家一起分析一下高博的单目稠密重建的代码，有了前三篇文章的理论铺垫，相信你读起来下一篇文章中的代码会如鱼得水。

我们下一期再见！