数学归纳法:搞定循环与递归的钥匙
1. 温故知新:数学归纳法
计算机的本质,是一个用来计算的工具,它最开始就是帮助我们完成一些现实世界里面的计算任务,并且完成的又快又好。那么现实世界的问题,是如何转换成可以在计算机中计算的任务呢?这个转换的过程中,都有哪些必不可少的东西呢?
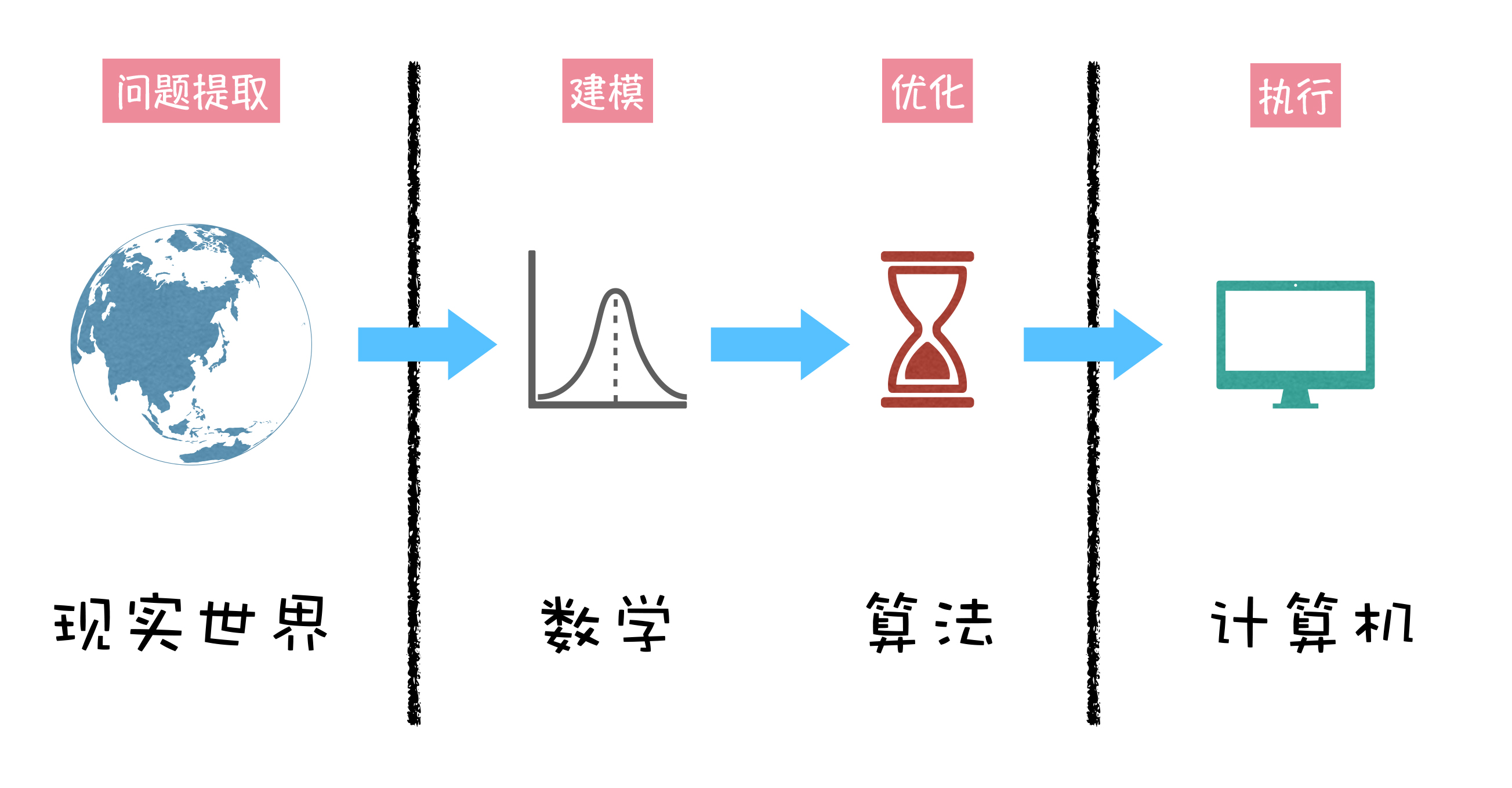
在这幅图中,我们把转换过程分成四个部分:“现实世界”“数学”“算法”和“计算机”。这四个部分形成了一个路线,也就是从现实世界中的实际问题,到计算机中的可计算任务的过程。
现实世界中的问题,本质是可以计算的,也就是说实际问题都可以做数学建模。
算法是将数学问题,转换到计算机中的计算任务的桥梁。
计算机的核心是算法,算法的核心是数学。

其实数学归纳法的三个步骤,总结起来就是,有一个已知正确的初始状态,然后证明如果前一个状态成立,那么后一个状态也成立(这一步主要在做过程正确性的证明),最后就是得出结论,在这个初识状态和转移过程的正确保证下,所有问题中的状态都成立。
第一步,验证边界条件,第一块多米诺骨牌倒下了。
第二步,就是假设,第 n 块倒下了,根据多米诺骨牌的结构性质,那么如果存在 n + 1 块,第 n + 1 块也一定会倒下。
第三步,得出结论,只要第一块倒了,所有的多米诺骨牌都会倒下。
2. 深入浅出:理解递归函数
什么是递归呢?递归是一种编程技巧。
递归程序设计中的重要的两部分:边界条件和处理过程
- 所谓边界条件,就是当递归函数中的参数等于多少的时候,可以直接返回的条件。
- 处理过程呢,就是设计程序过程,处理递归调用的返回结果,根据递归调用的返回结果,得到本函数的结果。
总结
- 数学归纳法中重要的两部分,一是要边界条件成立,二是证明转移过程成立。
- 程序设计最重要的是正确性,递归函数的正确性可以利用数学归纳法来保证。