(三)tensorflow-gpu2.0之线性模型

摘要：通过一个简单的实例，说明线性回归的工作原理。首先需要假定一个线性模型（如y=aX**2+b，a和b就是这个模型的权重和偏置），假设给定一定数量的已知数据，因变量通过预测模型得到一个预测值，这个预测值与真实值之间的存在误差，当这个误差足够小，此时对应的a和b的值作为训练好的模型参数。

BP神经网络的理论推导过程中解释了，正向传播和反向传播的详细工作过程。（参考资料：https://www.cnblogs.com/liuhuacai/p/11973036.html）

1.训练集

　　如下图所示的数据集（离散点），这些数据集之间存在什么样的关系。从大体上看，这个数据集像一个一元二次函数，但是我们并不清楚这个函数的具体表达式。这里有两个关键点：

　　1>一元二次函数

　　2>不知具体表达式

　　然而，在实际数据中，我们大概率的不知道这个数据整体满足什么样的函数关系式。因此，我们先用一个一元二次方程进行回归分析（了解实现过程），之后再用多项式方程进行回归分析（虽然多项式也并不能完全表达，但是其更接近实际情况）

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
##1.训练数据准备:y=x**2+1加入噪声，作为训练数据
data = []
x_data = []
y_data = []
for i in range(1000):##这里循环1000次，生成1000个采样点
    x = np.random.uniform(-1.,1.)
    y = x**2+1+np.random.normal(0.,0.1)##加入高斯噪声，均值0.，方差为0.01
    data.append([x,y])
    x_data.append(x)
    y_data.append(y)
data = np.array(data)
plt.scatter(x_data,y_data, s=20, c="#ff1212", marker='o')
plt.ylabel('y',fontproperties = 'SimHei',fontsize = 20)
plt.xlabel('x',fontproperties = 'SimHei',fontsize = 20)
plt.title('训练集',fontproperties = 'SimHei',fontsize = 30)
plt.legend()
plt.show()

2.正向传播

　　我们假定一个预测模型为y=a*x**2+b,给定任意的初始值a,b作为原始预测模型（后续通过不断更新a,b的值，来修正这个模型）。正向传播的目的：通过数据集上的已知点，计算已知结果（已知点的y值）与预测结果的误差（预测结果：已知的x带入预测模型得到的值）。

def forward(a,b,data):
    totalEoor = 0
    for i in range(0,len(data)):
        x = data[i,0]                    ##已知点x
        y = data[i,1]                    ##已知点y
        totalEoor +=(y-(a*x**2+b))**2    ##a*x**2+b当前预测值，此处计算差的平方，并累加
    ##将累计误差求平均值，得到均方差
    return totalEoor / float(len(data))

3.计算梯度

　　梯度的求导过程如下图所示，总误差对a,b的导数（其它视作常量）

　　

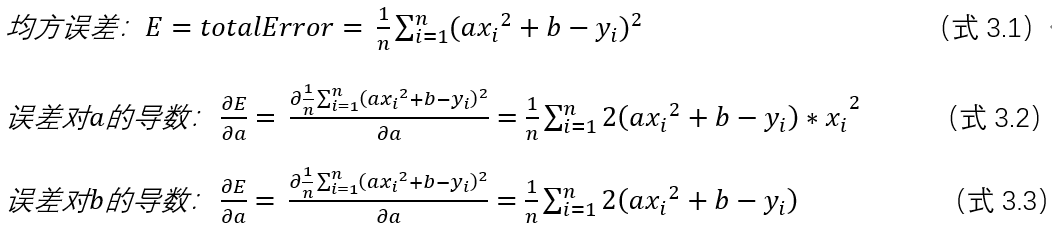
##3.计算梯度
def step_gradient(a_currunt,b_current,data,lr): ##data训练集，lr学习率
    a_gradient = 0
    b_gradient = 0
    n  = float(len(data))
    for i in range(0,len(data)):
        x = data[i, 0]  ##已知点x
        y = data[i, 1]  ##已知点y
        ##计算总误差对a到梯度
        a_gradient +=(2/n)*(a_currunt*x**2+b_current-y)*x**2
        ##计算总误差对b到梯度
        b_gradient += (2 / n) * (a_currunt * x ** 2 + b_current - y)

        ##通过梯度下降计算，下一状态的a和b
        new_a = a_currunt-(lr*a_gradient)
        new_b = b_current-(lr*b_gradient)
        return [new_a,new_b]

4.梯度更新（此处详见BP神经网络推导过程，文首有链接）

##4.梯度更新
    def gradient_descent(data,start_a,start_b,lr,num_iter):
        a = start_a
        b = start_b
        for step in range(num_iter):
            a,b = step_gradient(a,b,data,lr)
            loss = forward(a,b,data)
            if step%50 == 0:
                print(f"iteration:{step},loss:{loss},a:{a},b:{b}")
        return [a,b]

5.实现该线性回归的完整代码

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
'''
线性回归的关键点：
1.足够数量的训练数据
2.前向传播的误差计算
3.反向传播的梯度计算
4.反向传播的梯度更新
备注：BP神经网络的理论推导过程见另一篇博文
说明：训练模型的目的是获得最佳的权重和偏置值，通过梯度下降法，不断更新权重和偏置，最终获得预测模型
1.先默认给一个权重和偏置（初始预测模型）
2.计算训练数据与初始预测模型预测结果的误差
3.通过误差对权重和偏置求梯度
4.通过梯度更新权重和偏置，得到新的预测模型
5.重复2-4步骤，直到误差达到足够小，即得到最终的预测模型
'''
##1.训练数据准备:y=x**2+1加入噪声，作为训练数据
data_pra = []
x_data = []
y_data = []
for i in range(1000):##这里循环1000次，生成1000个采样点
    x = np.random.uniform(-1.,1.)
    y = x**2+1+np.random.normal(0.,0.1)##加入高斯噪声，均值0.，方差为0.01
    data_pra.append([x,y])
    x_data.append(x)
    y_data.append(y)
data_pra = np.array(data_pra)
# plt.scatter(x_data,y_data, s=20, c="#ff1212", marker='o')
# plt.ylabel('y',fontproperties = 'SimHei',fontsize = 20)
# plt.xlabel('x',fontproperties = 'SimHei',fontsize = 20)
# plt.title('训练集',fontproperties = 'SimHei',fontsize = 30)
# plt.legend()
# plt.show()

##2.计算误差：每个点的预测值与真实值之间的平方误差累加，获得训练集上的均方误差。
def mse(a,b,data):
    totalEoor = 0
    for i in range(0,len(data)):
        x = data[i,0]                    ##已知点x
        y = data[i,1]                    ##已知点y
        totalEoor +=(y-(a*x**2+b))**2    ##a*x**2+b当前预测值，此处计算差的平方，并累加
    ##将累计误差求平均值，得到均方差
    return totalEoor / float(len(data))
##3.计算梯度
def step_gradient(a_currunt,b_current,data,lr): ##data训练集，lr学习率
    a_gradient = 0
    b_gradient = 0
    n  = float(len(data))
    for i in range(0,len(data)):
        x = data[i, 0]  ##已知点x
        y = data[i, 1]  ##已知点y
        ##计算总误差对a到梯度
        a_gradient +=(2/n)*(a_currunt*x**2+b_current-y)*x**2
        ##计算总误差对b到梯度
        b_gradient += (2 / n) * (a_currunt * x ** 2 + b_current - y)

        ##通过梯度下降计算，下一状态的a和b
        new_a = a_currunt-(lr*a_gradient)
        new_b = b_current-(lr*b_gradient)
        return [new_a,new_b]

##4.梯度更新
def gradient_descent(data,start_a,start_b,lr,num_iter):
    a = start_a
    b = start_b
    for step in range(num_iter):
        a,b = step_gradient(a,b,data,lr)
        loss = mse(a,b,data)
        if step%50 == 0:
            print(f"iteration:{step},loss:{loss},a:{a},b:{b}")
    return [a,b]
def main():
    lr = 0.1##学习率
    initial_a = 1.2
    initial_b = 2
    num_iter = 100000
    [a,b] = gradient_descent(data_pra,initial_a,initial_b,lr,num_iter)
    loss = mse(a,b,data_pra)
    print(f'loss:{loss},a:{a},b:{b}')
if __name__ == '__main__':
    main()

6.运行结果分析

iteration:35350,loss:0.015599832320452396,a:1.1954485957169838,b:0.9742178239825664
iteration:35400,loss:0.015598969390681304,a:1.195448557215267,b:0.9742091465783564
iteration:35450,loss:0.015598115197044205,a:1.1954485190966948,b:0.9742005555260452
iteration:35500,loss:0.01559726964965752,a:1.195448481357453,b:0.9741920499663144
iteration:35550,loss:0.015596432659590657,a:1.1954484439937678,b:0.9741836290483971
iteration:35600,loss:0.015595604138855211,a:1.195448407001902,b:0.9741752919299927
iteration:35650,loss:0.015594784000394428,a:1.1954483703781558,b:0.974167037777183

iteration:99750,loss:0.015513872837423056,a:1.1954447267330348,b:0.9733458437061412
iteration:99800,loss:0.015513872835265523,a:1.195444726732935,b:0.9733458436840607
iteration:99850,loss:0.015513872833129468,a:1.195444726732835,b:0.9733458436622
iteration:99900,loss:0.015513872831014526,a:1.195444726732735,b:0.9733458436405569
iteration:99950,loss:0.015513872828920576,a:1.1954447267326351,b:0.973345843619129

从iteration：35350开始loss值就是0.0155，到迭代结束iteration：99950 loss值还是0.0155，为什么这6万次的迭代没有降低误差呢？

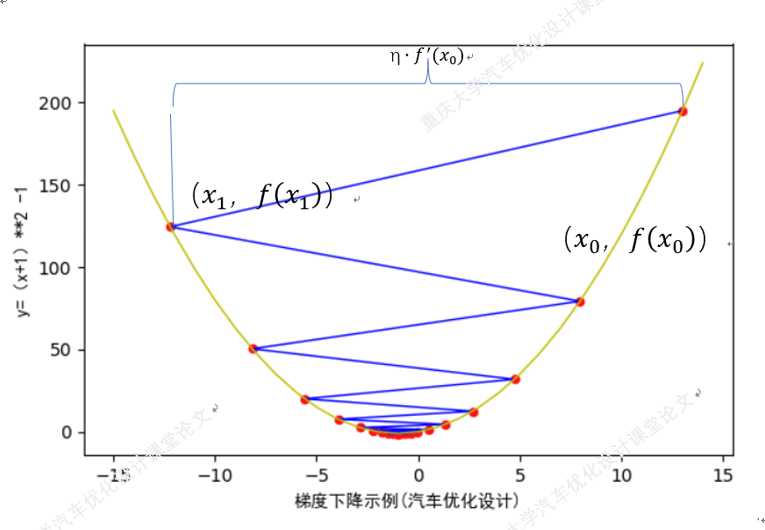
我们从梯度下降的原理着手分析：梯度下降法的运行轨迹如下图所示（参考资料https://www.cnblogs.com/liuhuacai/p/11973036.html）

如果梯度更新的步长过大，有可能出现梯度更新时，出现左右摆动而不能达到最小值的情况。（梯度下降法更新梯度越靠近内测，效率越低，深刻可能出现梯度爆炸的情况。）

 解决方案1：减小学习率  将学习率调整到0.01

iteration:99050,loss:0.016146801388219667,a:1.0715538518082957,b:1.0525016042319189
iteration:99100,loss:0.016122305316709693,a:1.0715337966809884,b:1.0523536651833887
iteration:99150,loss:0.016097882047442086,a:1.0715137619671822,b:1.0522058767174955
iteration:99200,loss:0.01607353140891555,a:1.0714937476460986,b:1.0520582386809658
iteration:99250,loss:0.016049253230001503,a:1.0714737536969805,b:1.051910750920681
iteration:99300,loss:0.01602504733994341,a:1.071453780099092,b:1.05176341328368
iteration:99350,loss:0.016000913568355722,a:1.0714338268317198,b:1.0516162256171544
iteration:99400,loss:0.015976851745224098,a:1.0714138938741686,b:1.0514691877684585
iteration:99450,loss:0.015952861700902866,a:1.0713939812057653,b:1.0513222995850953
iteration:99500,loss:0.015928943266115474,a:1.071374088805858,b:1.0511755609147246
iteration:99550,loss:0.015905096271953398,a:1.0713542166538164,b:1.051028971605161
iteration:99600,loss:0.01588132054987588,a:1.071334364729032,b:1.0508825315043764
iteration:99650,loss:0.015857615931708084,a:1.071314533010915,b:1.0507362404604943
iteration:99700,loss:0.01583398224964124,a:1.071294721478897,b:1.0505900983217955
iteration:99750,loss:0.0158104193362315,a:1.071274930112432,b:1.050444104936713
iteration:99800,loss:0.01578692702439933,a:1.0712551588909944,b:1.050298260153836
iteration:99850,loss:0.015763505147428348,a:1.0712354077940787,b:1.0501525638219054
iteration:99900,loss:0.01574015353896525,a:1.0712156768012013,b:1.0500070157898183
iteration:99950,loss:0.015716872033018504,a:1.0711959658918981,b:1.0498616159066254

从结果分析，在第99950次迭代的时候损失值并没有明显的降低。但是可以看出，此时的loss值还在继续下降（上面时0.0155时，loss一直不下降）

解决方案二：增加迭代步数

iteration:134050,loss:0.009879049443214306,a:1.0615099188313872,b:0.9784113296942267
iteration:134100,loss:0.00987880513284394,a:1.0615000871164961,b:0.9783388048718202
iteration:134150,loss:0.009878572575364288,a:1.061490265409008,b:0.9782663538702139
iteration:134200,loss:0.009878351735404826,a:1.061480453698735,b:0.9781939766142678
iteration:134250,loss:0.009878142577678602,a:1.061470651975503,b:0.9781216730289182
iteration:134300,loss:0.009877945066982101,a:1.0614608602291453,b:0.9780494430391786
iteration:134350,loss:0.009877759168195135,a:1.0614510784495068,b:0.9779772865701379
iteration:134400,loss:0.009877584846280518,a:1.0614413066264428,b:0.9779052035469619
iteration:134450,loss:0.00987742206628409,a:1.0614315447498188,b:0.9778331938948922
iteration:134500,loss:0.009877270793334302,a:1.061421792809511,b:0.9777612575392466
iteration:134550,loss:0.009877130992642173,a:1.0614120507954055,b:0.9776893944054187
iteration:134600,loss:0.009877002629501157,a:1.0614023186973973,b:0.977617604418879
iteration:134650,loss:0.009876885669286788,a:1.061392596505395,b:0.9775458875051721
iteration:134700,loss:0.009876780077456685,a:1.0613828842093145,b:0.9774742435899202
iteration:134750,loss:0.009876685819550235,a:1.061373181799083,b:0.9774026725988201
iteration:134800,loss:0.009876602861188527,a:1.0613634892646384,b:0.9773311744576444
iteration:134850,loss:0.009876531168074115,a:1.0613538065959283,b:0.9772597490922417
iteration:134900,loss:0.009876470705990788,a:1.0613441337829115,b:0.9771883964285354
iteration:134950,loss:0.009876421440803534,a:1.0613344708155548,b:0.9771171163925245
iteration:135000,loss:0.00987638333845821,a:1.0613248176838375,b:0.9770459089102844
iteration:135050,loss:0.009876356364981487,a:1.0613151743777485,b:0.9769747739079637
iteration:135100,loss:0.009876340486480588,a:1.0613055408872856,b:0.9769037113117879
iteration:135150,loss:0.009876335669143161,a:1.0612959172024583,b:0.976832721048057
iteration:135200,loss:0.0098763418792371,a:1.0612863033132858,b:0.9767618030431462
iteration:135250,loss:0.009876359083110338,a:1.0612766992097977,b:0.9766909572235051
iteration:135300,loss:0.009876387247190737,a:1.0612671048820326,b:0.9766201835156584
iteration:135350,loss:0.00987642633798581,a:1.061257520320041,b:0.9765494818462058
iteration:135400,loss:0.00987647632208263,a:1.0612479455138808,b:0.9764788521418222
iteration:135450,loss:0.009876537166147687,a:1.0612383804536243,b:0.9764082943292561
iteration:135500,loss:0.009876608836926605,a:1.06122882512935,b:0.9763378083353311

增加迭代步数，loss值下降到了0.0098，但是此后不能继续下降。

学习率过低，计算时间和计算量却增加了不少。

解决方案三：是否时数据本身的误差就很大呢？在方案二的基础上调整噪声的方差（缩小10倍）

    y = x**2+1+np.random.normal(0.,0.001)##加入高斯噪声，均值0.，方差为0.01

iteration:287050,loss:3.9431556454632605e-05,a:1.0063919298163915,b:1.003793957193313
iteration:287100,loss:3.9397361754980635e-05,a:1.006391409298289,b:1.0037912788789307
iteration:287150,loss:3.936321878138548e-05,a:1.0063908893200904,b:1.0037886033426102
iteration:287200,loss:3.932912744649047e-05,a:1.006390369881235,b:1.0037859305814705
iteration:287250,loss:3.929508766309385e-05,a:1.0063898509811644,b:1.0037832605926327
iteration:287300,loss:3.926109934414391e-05,a:1.0063893326193176,b:1.0037805933732211
iteration:287350,loss:3.922716240276282e-05,a:1.0063888147951388,b:1.0037779289203625

从结果来看，缩小原始数据本身的误差，可以继续缩小loss值。因此，loss不能继续降低有可能是数据本身误差就比较大

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
'''
线性回归的关键点：
1.足够数量的训练数据
2.前向传播的误差计算
3.反向传播的梯度计算
4.反向传播的梯度更新
备注：BP神经网络的理论推导过程见另一篇博文
说明：训练模型的目的是获得最佳的权重和偏置值，通过梯度下降法，不断更新权重和偏置，最终获得预测模型
1.先默认给一个权重和偏置（初始预测模型）
2.计算训练数据与初始预测模型预测结果的误差
3.通过误差对权重和偏置求梯度
4.通过梯度更新权重和偏置，得到新的预测模型
5.重复2-4步骤，直到误差达到足够小，即得到最终的预测模型
'''
##1.训练数据准备:y=x**2+1加入噪声，作为训练数据
data_pra = []
x_data = []
y_data = []
for i in range(1000):##这里循环1000次，生成1000个采样点
    x = np.random.uniform(-1.,1.)
    y = x**2+1+np.random.normal(0.,0.001)##加入高斯噪声，均值0.，方差为0.01
    data_pra.append([x,y])
    x_data.append(x)
    y_data.append(y)
data_pra = np.array(data_pra)
# plt.scatter(x_data,y_data, s=20, c="#ff1212", marker='o')
# plt.ylabel('y',fontproperties = 'SimHei',fontsize = 20)
# plt.xlabel('x',fontproperties = 'SimHei',fontsize = 20)
# plt.title('训练集',fontproperties = 'SimHei',fontsize = 30)
# plt.legend()
# plt.show()

##2.计算误差：每个点的预测值与真实值之间的平方误差累加，获得训练集上的均方误差。
def mse(a,b,data):
    totalEoor = 0
    for i in range(0,len(data)):
        x = data[i,0]                    ##已知点x
        y = data[i,1]                    ##已知点y
        totalEoor +=(y-(a*x**2+b))**2    ##a*x**2+b当前预测值，此处计算差的平方，并累加
    ##将累计误差求平均值，得到均方差
    return totalEoor / float(len(data))
##3.计算梯度
def step_gradient(a_currunt,b_current,data,lr): ##data训练集，lr学习率
    a_gradient = 0
    b_gradient = 0
    n  = float(len(data))
    for i in range(0,len(data)):
        x = data[i, 0]  ##已知点x
        y = data[i, 1]  ##已知点y
        ##计算总误差对a到梯度
        a_gradient +=(2/n)*(a_currunt*x**2+b_current-y)*x**2
        ##计算总误差对b到梯度
        b_gradient += (2 / n) * (a_currunt * x ** 2 + b_current - y)

        ##通过梯度下降计算，下一状态的a和b
        new_a = a_currunt-(lr*a_gradient)
        new_b = b_current-(lr*b_gradient)
        return [new_a,new_b]

##4.梯度更新
def gradient_descent(data,start_a,start_b,lr,num_iter):
    a = start_a
    b = start_b
    for step in range(num_iter):
        a,b = step_gradient(a,b,data,lr)
        loss = mse(a,b,data)
        if step%50 == 0:
            print(f"iteration:{step},loss:{loss},a:{a},b:{b}")
        if loss<0.00001:
            break
    return [a,b],lr
def main():
    lr = 0.01##学习率
    initial_a = 1.2
    initial_b = 2
    num_iter = 100000000000000000
    [a,b] = gradient_descent(data_pra,initial_a,initial_b,lr,num_iter)
    loss = mse(a,b,data_pra)
    print(f'loss:{loss},a:{a},b:{b}')
if __name__ == '__main__':
    main()