后缀数组被称为字符串处理神器,要解决字符串问题,一定要掌握它。(我这里的下标全部都是从1开始)
首先后缀数组要处理出两个数组,一个是sa[],sa[i]表示排名第i为的后缀的起始位置是什么,rank[i]表示第i个字符为起始点的后缀,它的排名是什么。可以知道sa[rank[i]] = i; rank[sa[i]] = i;

由于每个后缀各不相同,至起码长度不同,所以每个后缀是不可能相等的。
解除一个值,就能在O(n)时间内得到另外一个。
定义:suffix(i)表示从[i, lenstr]这个后缀。
普通排序复杂度显然是O(n^2),因为快排最坏情况也是O(n^2)。考虑运用字符串的特点?。这里考虑倍增法。为什么能用倍增呢?因为它充分利用了前面已经得到的信息。因为字符串的比较,都是从头到尾比较的,那么如果已经知道一个字符串前len / 2部分的比较结果,对于后加进来的后len / 2部分,还需要继续比较前len / 2部分吗?答案是不用的。所以,考虑倍增,先得到1个字符自己的rank,然后考虑2个字符的时候,用后一个字符的rank来作为第二关键字,进行排序即可。
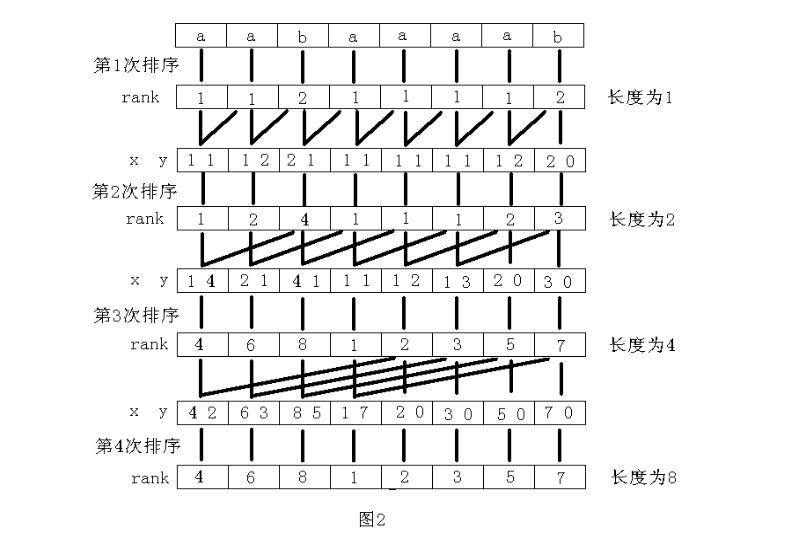
对关键字排序选用的是基数排序,因为它可以在O(n + maxnum)的时间内排好序。然后为了预防越界,就是aaaa这样,suffix(1)和suffix(2)比较的话,前3个都是匹配的,然后明显是"aaa",suffix(2)比较小,所以就在末尾加上一个0,来预防越界,也能解决排名问题。
关于后缀数组的字符数组为什么用int str[]这样:
ans:因为有时候解题的时候,需要把n个串连接起来,那么你每两个串之间就要加上一些不会出现的字符,来防止越界。
就是aaa%aaa%aaa这样是没用的,因为两个%会相等,使得LCP变大。aaa$aaa%aaa#才是正确的打开方式。
那么问题来了,n很大,1000个左右,你用char字符无能为力了,所以这个时候只能用int str[]了。
但是一般的题,都是1个或者两个字符串而已,用char str[]是足够的。
题目就是那个POJ 3294了。
book[]大小,用于基数排序,起码要大于lenstr,因为要记录rank[],而rank[]会有lenstr那么大

const int maxn = 20000 + 20; int a[maxn]; int sa[maxn]; int x[maxn]; int y[maxn]; int book[10000000 + 20]; bool cmp(int r[], int a, int b, int len) { return r[a] == r[b] && r[a + len] == r[b + len]; } void da(int str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; // 开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //倍增法求sa[],复杂度O(nlogn),p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //上面已经求出了第一个关键字了,现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个关键字是从sa[i]处拿的,排名靠前也正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键字保存的记录 //所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int rank[maxn]; int height[maxn]; //height[i]:表示suffix(sa[i - 1]) 和 suffix(sa[i]) 的LCP //就是两个排名紧挨着的后缀的LCP //sa[rank[i]] = i; rank[sa[i]] = i; void CalcHight(int str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) rank[sa[i]] = i; int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[rank[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[rank[i]] = k; } return ; }
height[],height[i]表示suffix(sa[i])和suffix(sa[i - 1])的LCP
可知道,sa[1]是最后末尾那个0(因为字典序总是最小的),而它没有前一个后缀,所以height[1] = 0是一定的。同理,sa[2]和sa[1],也是没有交集的,因为sa[1]的开头就是那个0,所以height[2] = 0也是一定的。而相反,height[lenstr + 1]是有定义的,因为被0占据了sa[1],所以其他的后移一位。

int rank[maxn]; int height[maxn]; //height[i]:表示suffix(sa[i - 1]) 和 suffix(sa[i]) 的LCP //就是两个排名紧挨着的后缀的LCP //sa[rank[i]] = i; rank[sa[i]] = i; void CalcHight(int str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) rank[sa[i]] = i; int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[rank[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[rank[i]] = k; } return ; }
更多详细的,请看这篇文章,我忘记了是谁写的了,找不到原文,真的真的不好意思。sorry

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 5000 + 20; int wa[maxn],wb[maxn],wv[maxn],WS[maxn]; int sa[maxn]; char r[maxn]; int cmp(int *r,int a,int b,int l) { return r[a]==r[b]&&r[a+l]==r[b+l]; //就像论文所说,由于末尾填了0,所以如果r[a]==r[b]( //实际是y[a]==y[b]), //说明待合并的两个长为j的字符串,前面那个一定不包含末尾0, //因而后面这个的起始位置至多在0的位置,不会再靠后了,因而不会产生 //数组 //越界。 } //da函数的参数n代表字符串中字符的个数,这里的n里面是包括人为在 //字符串末尾添加的那个0的,但论文的图示上并没有画出字符串末尾的0。 //da函数的参数m代表字符串中字符的取值范围,是基数排序的一个参数, //如果原序列都是字母可以直接取128,如果原序列本身都是整数的话, //则m可以取比最大的整数大1的值。 void da(char *r,int *sa,int n,int m) { int i,j,p,*x=wa,*y=wb,*t; //以下四行代码是把各个字符(也即长度为1的字符串)进行基数排序, //如果不理解为什么这样可以达到基数排序的效果, //不妨自己实际用纸笔模拟一下,我最初也是这样才理解的。 for(i=0; i<m; i++) WS[i]=0; for(i=0; i<n; i++) WS[x[i]=r[i]]++; //x[]里面本意是保存各个后缀的rank值的,但是这里并没有去存储rank值, //因为后续只是涉及x[]的比较工作,因而这一步可以不用存储真实的rank值 //,能够反映相对的大小即可。 for(i=1; i<m; i++) WS[i]+=WS[i-1]; for(i=n-1; i>=0; i--) sa[--WS[x[i]]]=i; //i之所以从n-1开始循环,是为了保证在当字符串中有相等的字符串时, //默认靠前的字符串更小一些。 // for (int i = 0; i < n; ++i) { // cout << sa[i] << " "; // } //下面这层循环中p代表rank值不用的字符串的数量,如果p达到n,那么各个字符串的大小关系就已经明了了。 //j代表当前待合并的字符串的长度,每次将两个长度为j的字符串合并成一个长度为2*j的字符串, //当然如果包含字符串末尾具体则数值应另当别论,但思想是一样的。 //m同样代表基数排序的元素的取值范围 for(j=1,p=1; p<n; j*=2,m=p) { //以下两行代码实现了对第二关键字的排序 for(p=0,i=n-j; i<n; i++) y[p++]=i; //结合论文的插图,我们可以看到位置在第n-j至n的元素的第二关键字 //都为0,因此如果按第二关键字排序,必然这些元素都是排在前面的。 for(i=0; i<n; i++) if(sa[i]>=j) y[p++]=sa[i]-j; //结合论文的插图,我们可以看到,下面一行的第二关键字不为0的 //部分都是根据上面一行的排序结果得到的,且上一行中只有sa[i]>=j //的第sa[i]个字符串(这里以及后面指的“第?个字符串”不是按字典序 //排名来的,是按照首字符在字符串中的位置来的)的rank才会作为下 //一行的第sa[i]-j个字符串的第二关键字,而且显然按sa[i]的 //顺序rank[sa[i]]是递增的,因此完成了对剩余的元素的第二关键字的 //排序。 // for (int i = 0; i < p; ++i) { // cout << y[i] << " "; // } // cout << endl; //第二关键字基数排序完成后,y[]里存放的是按第二关键字排序的字符串下标 for(i=0; i<n; i++) wv[i]=x[y[i]]; //这里相当于提取出每个字符串的第一关键字(前面说过了x[]是 //保存rank值的,也就是字符串的第一关键字),放到wv[]里面是 //方便后面的使用 // for (int i = 0; i < n; ++i) { // cout << wv[i] << " "; // } // cout << endl; //以下四行代码是按第一关键字进行的基数排序 for(i=0; i<m; i++) WS[i]=0; for(i=0; i<n; i++) WS[wv[i]]++; for(i=1; i<m; i++) WS[i]+=WS[i-1]; for(i=n-1; i>=0; i--) sa[--WS[wv[i]]]=y[i]; //i之所以从n-1开始循环,含义同上,同时注意这里是y[i], //因为y[i]里面才存着字符串的下标 //下面两行就是计算合并之后的rank值了,而合并之后的rank值应该存 // 在x[]里面,但我们计算的时候又必须用到上一层的rank值, //也就是现在x[]里面放的东西,如果我既要从x[]里面拿, //又要向x[]里面放,怎么办?当然是先把x[]的东西放到另外一个 //数组里面,省得乱了。这里就是用交换指针的方式, //高效实现了将x[]的东西“复制”到了y[]中。 for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1; i<n; i++) x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; //这里就是用x[]存储计算出的各字符串rank的值了, //记得我们前面说过,计算sa[]值的时候如果字符串相同是 //默认前面的更小的,但这里计算rank的时候必须将相同 //的字符串看作有相同的rank,要不然p==n之后就不会再循环啦。 // cout << p << endl; } return; } //能够线性计算height[]的值的关键在于h[](height[rank[]])的性质, //即h[i]>=h[i-1]-1,下面具体分析一下这个不等式的由来。 //论文里面证明的部分一开始看得我云里雾里,后来画了一下终于搞明白了, //我们先把要证什么放在这:对于第i个后缀,设j=sa[rank[i] - 1], //也就是说j是i的按排名来的上一个字符串,按定义来i和j的最长公共前缀就 //是height[rank[i]],我们现在就是想知道height[rank[i]]至少是多少, //而我们要证明的就是至少是height[rank[i-1]]-1。 //好啦,现在开始证吧。 //首先我们不妨设第i-1个字符串(这里以及后面指的“第?个字符串” //不是按字典序排名来的,是按照首字符在字符串中的位置来的) //按字典序排名来的前面的那个字符串是第k个字符串,注意k不一定是i-2, //因为第k个字符串是按字典序排名来的i-1前面那个,并不是指在原字符串中 //位置在i-1前面的那个第i-2个字符串。 //这时,依据height[]的定义,第k个字符串和第i-1个字符串的公共前缀 //自然是height[rank[i-1]],现在先讨论一下第k+1个字符串和第i个字符串 //的关系。 //第一种情况,第k个字符串和第i-1个字符串的首字符不同, //那么第k+1个字符串的排名既可能在i的前面,也可能在i的后面, //但没有关系,因为height[rank[i-1]]就是0了呀,那么无论height[rank[i]] //是多少都会有height[rank[i]]>=height[rank[i-1]]-1, //也就是h[i]>=h[i-1]-1。 //第二种情况,第k个字符串和第i-1个字符串的首字符相同, //那么由于第k+1个字符串就是第k个字符串去掉首字符得到的, //第i个字符串也是第i-1个字符串去掉首字符得到的,那么显然 //第k+1个字符串要排在第i个字符串前面,要么就产生矛盾了。同时, //第k个字符串和第i-1个字符串的最长公共前缀是height[rank[i-1]], //那么自然第k+1个字符串和第i个字符串的最长公共前缀就是 //height[rank[i-1]]-1。 //到此为止,第二种情况的证明还没有完,我们可以试想一下, //对于比第i个字符串的字典序排名更靠前的那些字符串, //谁和第i个字符串的相似度最高(这里说的相似度是指 //最长公共前缀的长度)?显然是排名紧邻第i个字符串的那个字符串了呀, //即sa[rank[i]-1]。也就是说sa[rank[i]]和sa[rank[i]-1]的最长公共 //前缀至少是height[rank[i-1]]-1,那么就有 //height[rank[i]]>=height[rank[i-1]]-1,也即h[i]>=h[i-1]-1。 //证明完这些之后,下面的代码也就比较容易看懂了。 int rank[maxn],height[maxn]; void calheight(char *r,int *sa,int n) { int i,j,k=0; for(i=1; i<=n; i++) rank[sa[i]]=i; //计算每个字符串的字典序排名 for(i=0; i<n; height[rank[i++]]=k) //将计算出来的height[rank[i]]的值,也就是k,赋给height[rank[i]]。 //i是由0循环到n-1,但实际上height[]计算的顺序是由height[rank[0]] //计算到height[rank[n-1]]。 for(k?k--:0,j=sa[rank[i]-1]; r[i+k]==r[j+k]; k++); //上一次的计算结果是k,首先判断一下如果k是0的话, //那么k就不用动了,从首字符开始看第i个字符串和第j个字符串前 //面有多少是相同的,如果k不为0,按我们前面证明的,最长公共 //前缀的长度至少是k-1,于是从首字符后面k-1个字符开始检查起即 //可。 return; } //最后再说明一点,就是关于da和calheight的调用问题,实际上在“小罗”写的源程序里面是如下调用的, //这样我们也能清晰的看到da和calheight中的int n不是一个概念, //同时height数组的值的有效范围是height[1]~height[n]其中height[1]=0, //原因就是sa[0]实际上就是我们补的那个0,所以sa[1]和sa[0]的最长公共前 //缀自然是0。 void work () { strcpy(r,"1111111111"); int n = strlen(r); r[n]=0; da(r,sa,n+1,128); for (int i = 0; i < n + 1; ++i ) { cout << sa[i] << " "; } cout << endl; calheight(r,sa,n); for (int i = 0; i < n; ++i) { cout << rank[i] << " "; } cout << endl; for (int i = 0; i < n; ++i) { cout << height[i] << " "; } cout << endl; } int main () { work (); return 0; }
Question 1:
如果求任意给定后缀suffix(i)和suffix(j)的LCP?
ansLCP = min (height[rank[i] + 1],....height[j]);
例如:aabaaaab

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 4000 + 20; char str[maxn]; int sa[maxn], x[maxn], y[maxn], book[300]; bool cmp(int r[], int a, int b, int len) { return r[a] == r[b] && r[a + len] == r[b + len]; } void da(char str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int RANK[maxn], height[maxn]; void CalcHight(char str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } void work() { scanf("%s", str + 1); int lenstr = strlen(str + 1); str[lenstr + 1] = '$'; str[lenstr + 2] = '�'; da(str, sa, lenstr + 1, 128); CalcHight(str, sa, lenstr + 1); cout << "sa: "; for (int i = 1; i <= lenstr + 1; ++i) { cout << sa[i] << " "; } cout << endl; cout << "rank: "; for (int i = 1; i <= lenstr + 1; ++i) { cout << RANK[i] << " "; } cout << endl; cout << "Height: "; for (int i = 1; i <= lenstr + 1; ++i) { cout << height[i] << " "; } cout << endl; for (int i = 1; i <= lenstr + 1; ++i) { cout << i << " "; for (int j = sa[i]; j <= lenstr + 1; ++j) { cout << str[j]; } cout << endl; } } int main() { #ifdef local freopen("data.txt","r",stdin); #endif work(); return 0; }
先输出东西看看。
假如我求suffix(2) 和 suffix(5)
本来是求suffix(sa[7])和suffix(sa[3])的,但是他们不相邻,无法直接height[i] O(1)出结果。
那么问题转化为
sa[4] 和 sa[3]
sa[5] 和 sa[4]
sa[6]和sa[5]
sa[7]和sa[6]即可啊。
一前以后,重叠的最小的就是答案。
题目也一并写在这里:
POJ 3261 Milk Patterns
http://poj.org/problem?id=3261
求出重复至少k次的字符串最大长度,可重叠的。
运用height[i]的定义,两个后缀之间的LCP,那么二分一个答案,如果有height[i] >= val,证明有两个串是这样重叠的,因为最起码也有一个吧,本来height[i] 就是两个串之间的比较。要用连续的height[i] >= val才行,因为可知道,height[i]是按sa来分的,这样的话,字典序差不多的,总会挨在一起,这样是刚好,是一定要这样,不然你2、3、2、3、2、3 + 4、6、4、6、4、6
这样,ans只能是4而已,因为后面那个重叠和前面那个重叠,是不一样的,可以说这里的height[]十分美妙。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> int n, k; const int maxn = 20000 + 20; int a[maxn]; int sa[maxn]; int x[maxn]; int y[maxn]; int book[10000000 + 20]; bool cmp(int r[], int a, int b, int len) { return r[a] == r[b] && r[a + len] == r[b + len]; } void da(int str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; // 开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //倍增法求sa[],复杂度O(nlogn),p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //上面已经求出了第一个关键字了,现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个关键字是从sa[i]处拿的,排名靠前也正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键字保存的记录 //所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int rank[maxn]; int height[maxn]; //height[i]:表示suffix(sa[i - 1]) 和 suffix(sa[i]) 的LCP //就是两个排名紧挨着的后缀的LCP //sa[rank[i]] = i; rank[sa[i]] = i; void CalcHight(int str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) rank[sa[i]] = i; int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[rank[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[rank[i]] = k; } return ; } bool check (int val) { //检查有多少个连续重叠val个字符的元素 int cnt = 1; for (int i = 3; i <= n + 1; ++i) { if (height[i] >= val) cnt++; else cnt = 1; if (cnt >= k) return true; } return false; } void work () { int mx = -inf; for (int i = 1; i <= n; ++i) { scanf ("%d", &a[i]); a[i]++; mx = max (a[i], mx); } a[n + 1] = 0; da (a, sa, n + 1, mx + 2); CalcHight (a, sa, n + 1); // for (int i = 1; i <= n; ++i) { // cout << sa[i] << " "; // } // cout << endl; // for (int i = 1; i <= n; ++i) { // cout << height[i] << " "; // } // cout << endl; // cout << check (9) << endl; int begin = 1, end = n; while (begin <= end) { int mid = (begin + end) >> 1; if (check (mid)) { begin = mid + 1; } else { end = mid - 1; } } cout << end << endl; return; } int main () { #ifdef local freopen("data.txt","r",stdin); #endif while (scanf ("%d%d", &n, &k) != EOF) work (); return 0; }
poj 1743 Musical Theme
http://poj.org/problem?id=1743
给定一个序列,求其中的最长的不重复序列,两个序列认为相同,前提是他们的公差是相同的。
思路:首先先把这个元素减去上一个元素,得到整个序列的公差,问题转化为求相同的序列中最长的那个。(至少出现两次)
先得到height[],首先二分长度val,对于height[i] >= val的,分为一组,(要求连续的,不连续的又重新开始,因为height[]是按字典序拍好的,如果遇到一个height[i] < k,那么后面的height[i] > k是一定和前面的height[i] > k不会相同的,如果相同,矛盾了,他们应该排在一起。),题目的问题是存在性问题,我二分一个答案val,只需要找到2个不重叠的串即可。那么就对每一个分组,记录一个mi和mx,表示这个分组中最小开始位置和最大开始位置,如果,mx - mi >= val,则证明val可行。为什么呢?
假如是1 2 3 4 5 6 7 8 9 10 ..... val是5,mi = 1, mx = 6,他们开始的,5个位置,绝对不会重叠。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 20000 + 20; int a[maxn]; int n; int sa[maxn], x[maxn], y[maxn], book[2000 + 20]; bool cmp(int r[], int a, int b, int len) { return r[a] == r[b] && r[a + len] == r[b + len]; } void da(int str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //倍增法求sa[],复杂度O(nlogn),p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int height[maxn]; int rank[maxn]; void CalcHight(int str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) rank[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[rank[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[rank[i]] = k; } return ; } bool check (int val) { int mi = inf, mx = -inf; for (int i = 3; i <= n; ++i) { if (height[i] >= val) { mi = min (mi, min(sa[i - 1],sa[i])); mx = max (mx, max(sa[i - 1],sa[i])); if (mx - mi >= val) return true; } else { mi = inf; mx = -inf; } } return false; } int gg[maxn]; void work () { for (int i = 1; i <= n; ++i) { scanf ("%d", &a[i]); } int fix = 100; int t = 0; int mx = -inf; for (int i = 2; i <= n; ++i) { gg[++t] = a[i] - a[i - 1] + fix; mx = max (mx, gg[t]); } gg[t + 1] = 0; da (gg, sa, t + 1, mx + 2); CalcHight (gg, sa, t + 1); int begin = 1, end = t; while (begin <= end) { int mid = (begin + end) >> 1; if (check (mid)) { begin = mid + 1; } else { end = mid - 1; } } if (end < 4) { printf ("0 "); } else { printf ("%d ", end + 1); } return ; } int main () { #ifdef local freopen("data.txt","r",stdin); #endif while (scanf ("%d", &n) != EOF && n) work (); return 0; }
不同子串个数
spoj 694 Distinct Substrings
求解[1,lentr]中不同子串的个数。一个字符串str,有n个后缀,那么有多少个子串呢?就是每个后缀的所有前缀,但题目求的是不同子串的个数,所以要去重。先按字典序拍好所有后缀,每个后缀,有lenstr - sa[i] + 1个后缀,然后重复了那些呢?重复了height[i]啊。所以ans就是lenstr - sa[i] + 1 - height[i]
假如样例:ABABA
后缀排名是:
0 0
A 0
ABA 1
ABABA 3
BA 0
BABA 2
减去height即可

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 1000 + 20; char str[maxn]; int sa[maxn], x[maxn], y[maxn], book[maxn]; bool cmp(int r[], int a, int b, int len) { return r[a] == r[b] && r[a + len] == r[b + len]; } void da(char str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int RANK[maxn]; int height[maxn]; void CalcHight(char str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } void work () { scanf ("%s", str + 1); int lenstr = strlen (str + 1); str[lenstr + 1] = 0; str[lenstr + 2] = '�'; da (str, sa, lenstr + 1, 128); CalcHight (str, sa, lenstr + 1); // for (int i = 1; i <= lenstr + 1; ++i) { // cout << sa[i] << " "; // } // cout << endl; int ans = 0; for (int i = 1; i <= lenstr + 1; ++i) { ans += lenstr - sa[i] + 1 - height[i]; } cout << ans << endl; return ; } int main () { #ifdef local freopen("data.txt","r",stdin); #endif int t; scanf ("%d", &t); while (t--) work (); return 0; }
其实这题可以用字符串hash做,只不过要一步一步算出来,区间内子串也要算出来

#include <cstdio> #include <cstdlib> #include <cstring> typedef unsigned long long int ULL; const int seed = 13131; // 31 131 1313 13131 131313 etc.. const int maxn = 2000+20; char str[maxn]; ULL powseed[maxn]; // seed的i次方 爆了也没所谓,sumHash的也爆。用了ULL,爆了也没所谓,也能唯一确定它,因为是无符号的 ULL sumHash[maxn]; //前缀hash值 int ans[maxn][maxn]; //ans[L][R]就代表ans,就是区间[L,R]内不同子串的个数 const int MOD = 10007; struct StringHash { int first[MOD+2],num; // 这里因为是%MOD ,所以数组大小注意,不是maxn ULL EdgeNum[maxn]; // 表明第i条边放的数字(就是sumHash那个数字) int next[maxn],close[maxn]; //close[i]表示与第i条边所放权值相同的开始的最大位置 //就比如baba,现在枚举长度是2,开始的时候ba,close[1] = 1;表明"ba"开始最大位置//是从1开始,然后枚举到下一个ba的时候,close[1]要变成3,开始位置从3开始了 void init () { num = 0; memset (first,0,sizeof first); return ; } int insert (ULL val,int id) //id是用来改变close[]的 { int u = val % MOD; //这里压缩了下标,val是一个很大的数字, for (int i = first[u]; i ; i = next[i]) //存在边不代表出现过,出现过要用val判断,val才是唯一的,边还是压缩后(%MOD)的呢 { if (val == EdgeNum[i]) //出现过了 { int t = close[i]; close[i] = id;//更新最大位置 return t; } } ++num; //没出现过的话,就加入图吧 EdgeNum[num] = val; // 这个才是精确的,只能用这个判断 close[num] = id; next[num] = first[u]; first[u] = num; return 0;//没出现过 } }H; void work () { scanf ("%s",str+1); int lenstr = strlen(str+1); for (int i=1;i<=lenstr;++i) sumHash[i] = sumHash[i-1]*seed + str[i]; memset(ans,0,sizeof(ans)); for (int L=1;L<=lenstr;++L) //暴力枚举子串长度 { H.init(); for (int i=1;i+L-1<=lenstr;++i) { int pos = H.insert(sumHash[i+L-1]-powseed[L]*sumHash[i-1],i); ans[i][i+L-1] ++; //ans[L][R]++,自己永远是一个 ans[pos][i+L-1]--; //pos放回0是没用的 //就像bababa,第二个ba的时候,会ans[1][4]--;表明[1,4]重复了一个 //然后第三个ba的时候,ans[2][6]--,同理,表明[2,6]也是重复了 //那么ans[1][6]重复了两个怎么算?就是在递推的时候,将ans[2][6]的值覆盖上来的 //ans[1][6] += ans[2][6] + ans[1][5] - ans[2][5]; } } for (int i = lenstr; i>=1; i--) { for (int j=i;j<=lenstr;j++) { ans[i][j] += ans[i+1][j]+ans[i][j-1]-ans[i+1][j-1]; } } printf ("%d ", ans[1][lenstr]); return ; } int main () { #ifdef local freopen("data.txt", "r", stdin); #endif powseed[0] = 1; for (int i = 1; i <= maxn-20; ++i) powseed[i] = powseed[i-1] * seed; int t; scanf ("%d",&t); while (t--) work(); return 0; }
ural 1297. Palindrome
http://acm.timus.ru/problem.aspx?space=1&num=1297
求一个串的最长回文子串

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 1000 + 20; char str[maxn * 2]; int p[maxn * 2]; int anspos; int manacher (char str[],int lenstr) { str[0]='*';//表示一个不可能的值 //目标要插入lenstr+1个'#',所以长度变成2*lenstr+1 for (int i=lenstr; i>=0; i--) { //str[lenstr+1]是'�' //i=lenstr时,i+i+2那个值要赋为'�'; //总长度只能是lenstr+lenstr+2,所以i从lenstr开始枚举 str[i+i+2]=str[i+1]; str[i+i+1]='#'; } int id=0,maxlen=0;//现在开始在str[2]了 anspos = 1; for (int i=2; i<=2*lenstr+1; i++) { //2*lenstr+1是'#'没用 if (p[id]+id>i) { //没取等号的,只能去到p[id]+id-1 p[i]=min(p[id]+id-i,p[2*id-i]); } else p[i]=1; //记得修改的是p[i] while (str[i+p[i]] == str[i-p[i]]) ++p[i]; if (p[id]+id<p[i]+i) id=i; // maxlen=max(maxlen,p[i]); if (maxlen < p[i]) { maxlen = p[i]; anspos = i; } } return maxlen-1; } char sub[maxn]; void work() { scanf("%s", str + 1); strcpy(sub + 1, str + 1); int lenstr = strlen(str + 1); int t = manacher(str, lenstr); // cout << anspos << endl; // cout << lenstr << endl; // cout << t << endl; anspos /= 2; if (t & 1) { int begin = anspos - (t - 1) / 2; int end = anspos + (t - 1) / 2; for (int i = begin; i <= end; ++i) { printf ("%c", sub[i]); } } else { int begin = anspos - t / 2 + 1; int end = anspos + t / 2; for (int i = begin; i <= end; ++i) { printf ("%c", sub[i]); } } printf (" "); return; } int main() { #ifdef local freopen("data.txt","r",stdin); #endif work(); return 0; }
后缀数组 + rmq
因为任何两个后缀,LCP = min(rank[i] + 1, ... rank[j])
rmq预处理,O(1)查询
先把这个串反过来放在后面,中间用个'$'隔开,免得重合。然后求一次后缀数组,即可得到不相交的后缀(LCP不会相交,因为'$'隔开了),奇数rmq rank[i] rank[all - i] 偶数 rank[i] rank[all - i + 1],画个图吧。aabaaaab
枚举每个起点作为中间点。即可

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 5000 + 20; char str[maxn]; int sa[maxn], x[maxn], y[maxn], book[2000 + 20]; bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] return r[a] == r[b] && r[a + len] == r[b + len]; } void da(char str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int RANK[maxn], height[maxn]; void CalcHight(char str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } int dp_min[maxn][30]; void init_RMQ (int n,int a[]) { //预处理->O(nlogn) for (int i=1; i<=n; ++i) { //dp_max[i][0] = a[i]; //自己 dp_min[i][0] = a[i]; //dp的初始化 } for (int j=1; j<20; ++j) { //先循环j,不取等号 for (int i=1; i+(1<<j)-1<=n; ++i) { //dp_max[i][j] = max(dp_max[i][j-1],dp_max[i+(1<<(j-1))][j-1]);//只用到上一维状态 dp_min[i][j] = min(dp_min[i][j-1],dp_min[i+(1<<(j-1))][j-1]); } } return ; } int RMQ_MIN (int begin,int end) { if (begin > end) { swap(begin, end); } begin++; int k = (int)floor(log2(end-begin+1.0)); return min(dp_min[begin][k],dp_min[end-(1<<k)+1][k]); } void work() { scanf("%s", str + 1); int lenstr = strlen(str + 1); str[lenstr + 1] = '$'; int to = lenstr; for (int i = lenstr + 2; i <= 2 * lenstr + 1; ++i) { str[i] = str[to--]; } str[2 * lenstr + 2] = 0; int up = 2 * lenstr + 2; da(str, sa, up, 300); CalcHight(str, sa, up); init_RMQ(up, height); int odd = 0, posodd; for (int i = 1; i <= lenstr; ++i) { int t = RMQ_MIN(RANK[i], RANK[up - i]); if (t > odd) { odd = t; posodd = i; } else if (t == odd && posodd > i) { //while(1); posodd = i; } } int even = 0, poseven; for (int i = 1; i <= lenstr; ++i) { int t = RMQ_MIN(RANK[i], RANK[up - i + 1]); if (t > even) { even = t; poseven = i; } else if (t == even && poseven > i) { //while (1); poseven = i; } } if (2 * odd - 1 >= 2 * even) { odd--; for (int i = posodd - odd; i <= posodd + odd; ++i) { cout << str[i]; } cout << endl; } else { for (int i = poseven - even; i <= poseven + even - 1; ++i) { cout << str[i]; } cout << endl; } } int main() { #ifdef local freopen("data.txt","r",stdin); #endif // printf ("%d ", '0'); work(); return 0; }
两个字符串的最长公共子串
POJ 2774 Long Long Message
http://poj.org/problem?id=2774
求两个串的最长公共子串
思路是把sub接在str后面,同样加一个'$'预防重叠,枚举每个i to lenstr + 1 + lensub + 1
判断sa[i] 和 sa[i - 1]是否在分别在两个串中,更新答案即可
下面这题一样的,就放一个代码算了
http://vjudge.net/problem/19283

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 100000 * 2 + 20; int sa[maxn], x[maxn], y[maxn], book[maxn + 20]; //book[]大小起码是lenstr,book[rank[]] bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] return r[a] == r[b] && r[a + len] == r[b + len]; } void da(char str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int RANK[maxn], height[maxn]; void CalcHight(char str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } char str[maxn], sub[maxn]; void work() { int n; cin >> n; scanf("%s%s", str + 1, sub + 1); int lenstr = strlen(str + 1); int lensub = strlen(sub + 1); str[lenstr + 1] = '$'; for (int i = lenstr + 2, t = 1; t <= lensub; ++t, ++i) { str[i] = sub[t]; } str[lenstr + 1 + lensub + 1] = 0; str[lenstr + 1 + lensub + 1 + 1] = '�'; da(str, sa, lenstr + 1 + lensub + 1, 128); CalcHight(str, sa, lenstr + 1 + lensub + 1); int pos, ans = 0; for (int i = 2; i <= lenstr + 1 + lensub + 1; ++i) { int mi = min(sa[i - 1], sa[i]); int mx = max(sa[i - 1], sa[i]); if (mi >= lenstr + 1 || mx <= lenstr) continue; if (ans < height[i]) { ans = height[i]; pos = sa[i]; } } for (int i = pos; ans; ++i, --ans) { printf("%c", str[i]); } return ; } int main() { #ifdef local freopen("data.txt","r",stdin); #endif work(); return 0; }
连续重复子串问题
poj 2406 Power Strings
http://poj.org/problem?id=2406
问一个串能否写成a^n次方这种形式。
虽然这题用kmp做比较合适,但是我们还是用后缀数组做一做,巩固后缀数组的能力。
对于一个串,如果能写出a^n这种形式,我们可以暴力枚举循环节长度L,那么后缀suffix(1)和suffix(1 + L)的LCP应该就是 lenstr - L。如果能满足,那就是,不能,就不是。
这题的话da算法还是超时,等我学了DC3再写上来。
其实这题可以不用枚举,考虑到如果能写成a^n这种形式,那么其循环节长度必定为 lenstr - height[rank[1]]
给个图可能会更清楚

如果是循环节,那么height[rank[1]]就是第1位的排名前后的lcp,肯定是第二个循环节那里的。
然后暴力判断一下就行~dc3, 2750ms才能卡过去

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 3 * 1000000 + 20; const int N = maxn; #define F(x) ((x)/3+((x)%3==1?0:tb)) #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) int r[maxn]; int wa[maxn],wb[maxn],wv[maxn],WS[maxn]; int sa[maxn]; int c0(int *r,int a,int b) { return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2]; } int c12(int k,int *r,int a,int b) { if(k==2) return r[a]<r[b]||r[a]==r[b]&&c12(1,r,a+1,b+1); else return r[a]<r[b]||r[a]==r[b]&&wv[a+1]<wv[b+1]; } void sort(int *r,int *a,int *b,int n,int m) { int i; for(i=0; i<n; i++) wv[i]=r[a[i]]; for(i=0; i<m; i++) WS[i]=0; for(i=0; i<n; i++) WS[wv[i]]++; for(i=1; i<m; i++) WS[i]+=WS[i-1]; for(i=n-1; i>=0; i--) b[--WS[wv[i]]]=a[i]; return; } void dc3(int *r,int *sa,int n,int m) { //涵义与DA 相同 int i,j,*rn=r+n,*san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p; r[n]=r[n+1]=0; for(i=0; i<n; i++) if(i%3!=0) wa[tbc++]=i; sort(r+2,wa,wb,tbc,m); sort(r+1,wb,wa,tbc,m); sort(r,wa,wb,tbc,m); for(p=1,rn[F(wb[0])]=0,i=1; i<tbc; i++) rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++; if(p<tbc) dc3(rn,san,tbc,p); else for(i=0; i<tbc; i++) san[rn[i]]=i; for(i=0; i<tbc; i++) if(san[i]<tb) wb[ta++]=san[i]*3; if(n%3==1) wb[ta++]=n-1; sort(r,wb,wa,ta,m); for(i=0; i<tbc; i++) wv[wb[i]=G(san[i])]=i; for(i=0,j=0,p=0; i<ta && j<tbc; p++) sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++]; for(; i<ta; p++) sa[p]=wa[i++]; for(; j<tbc; p++) sa[p]=wb[j++]; return; } int rank[maxn], height[maxn]; void calheight(int *r,int *sa,int n) { // 此处N为实际长度 int i,j,k=0; // height[]的合法范围为 1-N, 其中0是结尾加入的字符 for(i=1; i<=n; i++) rank[sa[i]]=i; // 根据SA求RANK for(i=0; i<n; height[rank[i++]] = k ) // 定义:h[i] = height[ rank[i] ] for(k?k--:0,j=sa[rank[i]-1]; r[i+k]==r[j+k]; k++); //根据 h[i] >= h[i-1]-1 来优化计算height过程 } char str[maxn]; void work() { int lenstr = strlen(str); for (int i = 0; i < lenstr; ++i) r[i] = str[i]; r[lenstr] = 0; dc3(r, sa, lenstr + 1, 128); calheight(r, sa, lenstr); int t = lenstr - height[rank[0]]; if (t == lenstr || lenstr % t != 0) { printf("1 "); } else { for (int i = t; i < lenstr; i += t) { for (int j = 0; j < t; ++j) { if (str[j] != str[i + j]) { printf("1 "); return; } } } printf("%d ", lenstr / t); } } int main() { #ifdef local freopen("data.txt","r",stdin); #endif while (scanf("%s", str) != EOF) { if (str[0] == '.') break; work(); } return 0; }
最长连续重复子串
SPOJ 687 RMQ + SA
找出一个串中的子串,这个子串具有最长的重复子串。例如abababab,这样ab重复了4次
思路:暴力枚举重复子串的单元串的长度L,就是上面的例子,单元串(“ab”)长度是2.
然后这样的话,如果是连续重复的,根据上一个题目,它的suffix(pos)和suffix(pos + L)的LCP是k的话,那么就是重复出现了
k / L + 1次。这个时候更新答案即可。例如ababab,pos=1,L=2.那么suffix(1)和suffix(3)的LCP是4,就是出现了3次了。
多了一个怎么办?abababa,这样LCP是5,但是5 / 2 + 1还是等于3,那就是多出来的那个,不够2,不够循环节,是没用的。
但是就判这个是会wa的。为什么呢?因为漏了情况,
考虑样例:babbabaabaabaabab。样例都过不了。因为枚举L = 3的时候,是枚举不到5这个开头的。就是pos不会去到等于5、
那怎么办呢?看看枚举到pos=7,L=3的时候,算出来的suffix(7)和suffix(10)的lcp = 7,这说明有一个是多余的 7 % 3 = 1
那么,就尝试着补2个字符给它(往左移动)看看这样的lcp会不会更大,更新答案即可。
因为出现多了一个的情况,就是出现7的情况,是因为少了个一头一尾,
例如: ABC | ABC | ABC| ABC 这样
你用pos=2去枚举了,L=3,就会得到LCP=11,需要往左再匹配一个A,看看能否变大。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 50000 + 20; char str[maxn]; int sa[maxn], x[maxn], y[maxn], book[maxn + 20]; //book[]大小起码是lenstr,book[rank[]] bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] return r[a] == r[b] && r[a + len] == r[b + len]; } void da(char str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int RANK[maxn], height[maxn]; void CalcHight(char str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } int dp_min[maxn][20]; void init_RMQ (int n,int a[]) { //预处理->O(nlogn) for (int i=1; i<=n; ++i) { dp_min[i][0] = a[i]; //dp的初始化 } for (int j=1; j<20; ++j) { //先循环j,不取等号 for (int i=1; i+(1<<j)-1<=n; ++i) { dp_min[i][j] = min(dp_min[i][j-1],dp_min[i+(1<<(j-1))][j-1]); } } return ; } int RMQ_MIN (int begin,int end) { // begin++; begin = RANK[begin]; end = RANK[end]; if (begin > end) swap(begin, end); begin++; int k = (int)floor(log2(end-begin+1.0)); return min(dp_min[begin][k],dp_min[end-(1<<k)+1][k]); } void work() { int lenstr; scanf("%d", &lenstr); for (int i = 1; i <= lenstr; ++i) { char ch[2]; scanf("%s", ch); str[i] = ch[0]; } str[lenstr + 1] = 0; str[lenstr + 2] = '�'; // printf("%s ", str + 1); da(str, sa, lenstr + 1, 128); CalcHight(str, sa, lenstr + 1); init_RMQ(lenstr + 1, height); int ans = 1; // cout << RMQ_MIN(5, 8) << endl; for (int i = 1; i <= lenstr; ++i) { for (int j = 1; j + i <= lenstr + 1; j += i) { int t = RMQ_MIN(j, j + i); int sum = t / i + 1; int pos = j - (i - t % i); //左移这么多个字符,使得补上这些字符 ans = max(ans, sum); if (pos >= 1 && pos + i <= lenstr + 1) { int t = RMQ_MIN(pos, pos + i); int sum = t / i + 1; ans = max(ans, sum); //尝试往左移动 } } } cout << ans << endl; return; } int main() { #ifdef local freopen("data.txt","r",stdin); #endif int t; scanf("%d", &t); while (t--) { work(); } return 0; }
多个字符串的重复子串。
POJ 3294
http://poj.org/problem?id=3294
给定n个串,n<=1000,要求找这n个串的共同出现过的子串,出现次数 >= n / 2 + 1才能作为贡献。
求最长的那个子串,若有多个,全部输出。
思路:可以把n个串和在一起,跑一次后缀数组,那么这个时候,相同排名的后缀就会排在一次。这时二分一个答案,表示子串的大小。那么就像以前的题一样,能把height[]分组了。对于heigh[i] >= mid的,放在一起,如果出现height[i] < mid,就证明不在同一组了,这个时候就要判断刚才那一组中,有多少个字符串是出现在不同的串中的,如果这个val > n / 2 + 1,那么这一组的解是可行的。怎么判断有多少个出现在不同的串呢?
1、串的长度是不同的。
2、你合并了,怎么判断呢?
方法就是用个id[u] = v,表示下标u是属于第v组的,那么合并的时候,把在同一个串中的下标分为第i组即可。
每一个可行组,选一个代表即可,不用全部保存到ans[]中。
注意数组用int str[],因为合并的时候中间的分割词不能相同,所以需要很大的数字

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 1000 * 1000 + 20; int str[maxn]; int sa[maxn], x[maxn], y[maxn], book[maxn]; //book[]大小起码是lenstr,book[rank[]] bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] return r[a] == r[b] && r[a + len] == r[b + len]; } void da(int str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int height[maxn], RANK[maxn]; void CalcHight(int str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } int n; char sub[1000 + 20]; int id[maxn], lenstr; int toch[maxn]; bool vis[1000 + 20]; bool solve(int len) { for (int i = 1; i <= n; ++i) vis[i] = false; int cnt = 0; for (int i = 1; i <= len; ++i) { if (!vis[id[toch[i]]]) { vis[id[toch[i]]] = true; cnt++; if (cnt >= n / 2 + 1) return true; } } return false; } int ans[maxn]; int lenans; bool check(int val) { int tol = 1; int lentoch = 0; bool flag = false; for (int i = 3; i <= lenstr + 1; ++i) { if (height[i] < val) { if (solve(lentoch)) { if (!flag) lenans = 0; ans[++lenans] = toch[1]; //每组选一个代表即可 flag = true; } lentoch = 0; } else { toch[++lentoch] = sa[i - 1]; toch[++lentoch] = sa[i]; } } if (lentoch) { if (solve(lentoch)) { if (!flag) lenans = 0; ans[++lenans] = toch[1]; flag = true; } lentoch = 0; } return flag; } void work() { lenstr = -1; int tem = 200; for (int i = 1; i <= n; ++i) { scanf("%s", sub + 1); str[++lenstr] = tem++; for (int j = 1; sub[j]; ++j) { str[++lenstr] = sub[j]; id[lenstr] = i; //这个位置是第几个字符串的 } } if (n == 1) { printf("%s ", sub + 1); return; } str[lenstr + 1] = 0; str[lenstr + 2] = '�'; da(str, sa, lenstr + 1, 2000); CalcHight(str, sa, lenstr + 1); int begin = 0, end = lenstr; while (begin <= end) { int mid = (begin + end) >> 1; if (check(mid)) { begin = mid + 1; } else { end = mid - 1; } } if (end == 0) { cout << "?" << endl; return; } for (int i = 1; i <= lenans; ++i) { for (int j = ans[i]; j <= ans[i] + end - 1; ++j) { printf("%c", str[j]); } printf(" "); } return ; } int main() { #ifdef local freopen("data.txt","r",stdin); #endif while (scanf("%d", &n) != EOF && n) { work(); printf(" "); } return 0; }
SPOJ 220 (坑了我很久,找了一天数据,分享一下)
PHRASES - Relevant Phrases of Annihilation
给定n个串,输出他们的最长公共子串,而且这个子串中在每个串中至少出现两次。
一开始的时候,想到的思路是和上题一样,二分一个答案,作为height[]的分组,分组的话很简单,原理就是连续的height[i] >= val的为一组,因为突然断了的话,子串是不会“全等”的,就是前面的"123"和"123"后缀相等,后面的"456"和"456"也相等,这样数值都是3,但是子串是不相同的。分好组后,我就学上题一样统计是否都来自这n个字符串中,就是每个字符串中都有这些子串。然后剩下的就是判断这个val,是否每个字符串中都包含了不相交的两个字符,长度是val的。这个可以用mx - mi >= val来判断,和以前的一题类似,也是对height[]分组了。(这个对height[]分组的思路很重要,几乎贯通了整个后缀数组),原因就是它排名前后的肯定会分在同一组,这些后缀都有很多共同性质,例如LCP最大等。
但是这个思路是错的。为什么呢?因为,如果有些字符串确实出现了,但是值却不是这个串得到的。
什么意思呢?
2
aghgibhag
agkjbghaha
考虑这个串,枚举2的时候,是可以得。因为它们都有ag,但是在第二个串中ag却只出现一次,反而ha出现了两次,这个ha替代了ag出现的次数,使得2成为一个可能答案。所以是错误思路。
然后我就有优化了一下,使得每个串的子串至少出现两次,才算作在这个串中出现过,那不行了吗?
就是上面的ag在第二个串没有出现过2次,所以不是答案。
但是这又是错误的思路,为啥
同理的,用些重叠的字符串来使得出现两次,然而重叠了无法成为答案就行。
2
aaaaaajkjkjkjk
aaaaaahwhwhwhw
aaaaaa使得4成为答案,然而4确是后面的两个串弄来的。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 10 * 10000 * 10 + 20; int sa[maxn], x[maxn], y[maxn], book[maxn]; //book[]大小起码是lenstr,book[rank[]] int subSa[13][10000 + 20]; bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] return r[a] == r[b] && r[a + len] == r[b + len]; } void da(int str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int RANK[maxn], height[maxn], subRank[13][10000 + 20], subHeight[13][10000 + 20]; void CalcHight(int str[], int sa[], int lenstr, int RANK[], int height[]) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } int n; char sub[13][10000 + 20]; int intSub[13][10000 + 20]; int lensub[13], id[maxn]; int str[maxn]; int lenstr; int vis[10 + 20]; bool CheckVal(int val) { for (int i = 1; i <= n; ++i) { bool flag = false; int mi = inf, mx = -inf; for (int j = 3; j <= lensub[i] + 1; ++j) { if (subHeight[i][j] >= val) { // mi = min(mi, subSa[i][j]); // mx = max(mx, subSa[i][j]); mi = min(mi, min(subSa[i][j - 1], subSa[i][j])); mx= max(mx, max(subSa[i][j - 1], subSa[i][j])); if (mx - mi >= val) { flag = true; break; } } else { // mi = mx = subSa[i][j]; mi = inf; mx = -inf; } } if (flag == false) return false; } return true; } bool solve(int arr[], int val, int lenarr) { // if (begin == end) return false; for (int i = 1; i <= n; ++i) { vis[i] = 0; } int cnt = 0; for (int i = 1; i <= lenarr; ++i) { if (vis[id[arr[i]]] < 2) { vis[id[arr[i]]]++; if (vis[id[arr[i]]] == 2) cnt++; if (cnt == n) { // cout << " fff " << endl; return CheckVal(val); } } } return false; } int arr[maxn]; int lenarr; int ans[maxn]; bool check(int val) { lenarr = 0; for (int i = 3; i <= lenstr + 1; ++i) { if (height[i] >= val) { arr[++lenarr] = sa[i]; arr[++lenarr] = sa[i - 1]; } else { if (solve(arr, val, lenarr)) { ans[1] = arr[1]; return true; } lenarr = 0; } } if (lenarr) { if (solve(arr, val, lenarr)) { ans[1] = arr[1]; return true; } } return false; } void work() { lenstr = -1; int tem = 200; scanf("%d", &n); for (int i = 1; i <= n; ++i) { scanf("%s", sub[i] + 1); lensub[i] = strlen(sub[i] + 1); str[++lenstr] = i; // id[lenstr] = i; for (int j = 1; sub[i][j]; ++j) { str[++lenstr] = sub[i][j]; intSub[i][j] = sub[i][j]; id[lenstr] = i; } intSub[i][lensub[i] + 1] = 0; } str[lenstr + 1] = 0; str[lenstr + 2] = '�'; da(str, sa, lenstr + 1, 2000); CalcHight(str, sa, lenstr + 1, RANK, height); for (int i = 1; i <= n; ++i) { da(intSub[i], subSa[i], lensub[i] + 1, 2000); CalcHight(intSub[i], subSa[i], lensub[i] + 1, subRank[i], subHeight[i]); } // for (int i = 1; i <= n; ++i) { // for (int j = 1; j <= lensub[i] + 1; ++j) { // cout << subRank[i][j] << " "; // } // cout << endl; // } // cout << "******debug******" << endl; // for (int i = 1; i <= n; ++i) { // printf("%s ", sub[i] + 1); // } //// for (int i = 1; i <= lenstr + 1; ++i) { //// cout << height[i] << " "; //// } //// cout << endl; // cout << CheckVal(2) << endl; // cout << "******EndDebug********" << endl; int begin = 0, end = lenstr + 1; while (begin <= end) { int mid = (begin + end) >> 1; if (check(mid)) { begin = mid + 1; } else { end = mid - 1; } // cout << mid << " " << check(mid) << endl; } //end = max(end, 0); cout << end << endl; for (int i = ans[1]; i <= ans[1] + end - 1; ++i) { printf("%c", str[i]); } cout << endl; return ; } int main() { #ifdef local freopen("data.txt","r",stdin); #endif int t; scanf("%d", &t); while (t--) { work(); } return 0; }
那么解决思路就是使得每个串中都存在两个不相交的子串,这个子串又是要相等的。
那么可以用mi[id]表示第id个串的最小位置,mx[id],然后不断更新这两个,在height[]分组的时候就一起算起来。
这样就不会被后面的字符串影响了。

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 10 * 10000 * 10 + 20; int sa[maxn], x[maxn], y[maxn], book[maxn]; //book[]大小起码是lenstr,book[rank[]] int subSa[13][10000 + 20]; bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] return r[a] == r[b] && r[a + len] == r[b + len]; } void da(int str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int RANK[maxn], height[maxn], subRank[13][10000 + 20], subHeight[13][10000 + 20]; void CalcHight(int str[], int sa[], int lenstr, int RANK[], int height[]) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } int n; char sub[13][10000 + 20]; int intSub[13][10000 + 20]; int lensub[13], id[maxn]; int str[maxn]; int lenstr; int vis[10 + 20]; int mi[10 + 20], mx[10 + 20]; void init() { for (int i = 0; i <= n; ++i) { mi[i] = inf; mx[i] = -inf; } return; } bool check(int val) { init(); for (int i = 3; i <= lenstr + 1; ++i) { if (height[i] >= val) { //更新val mi[id[sa[i]]] = min(mi[id[sa[i]]], sa[i]); mi[id[sa[i - 1]]] = min(mi[id[sa[i - 1]]], sa[i - 1]); mx[id[sa[i]]] = max(mx[id[sa[i]]], sa[i]); mx[id[sa[i - 1]]] = max(mx[id[sa[i - 1]]], sa[i - 1]); } else { int j; for (j = 1; j <= n; ++j) { if (mx[j] - mi[j] < val) break; } if (j == n + 1) return true; init(); } } for (int i = 1; i <= n; ++i) { if (mx[i] - mi[i] < val) return false; } return true; } void work() { lenstr = -1; int tem = 200; scanf("%d", &n); for (int i = 1; i <= n; ++i) { scanf("%s", sub[i] + 1); lensub[i] = strlen(sub[i] + 1); str[++lenstr] = i; // id[lenstr] = i; for (int j = 1; sub[i][j]; ++j) { str[++lenstr] = sub[i][j]; intSub[i][j] = sub[i][j]; id[lenstr] = i; } intSub[i][lensub[i] + 1] = 0; } str[lenstr + 1] = 0; str[lenstr + 2] = '�'; da(str, sa, lenstr + 1, 2000); CalcHight(str, sa, lenstr + 1, RANK, height); // for (int i = 1; i <= n; ++i) { // da(intSub[i], subSa[i], lensub[i] + 1, 2000); // CalcHight(intSub[i], subSa[i], lensub[i] + 1, subRank[i], subHeight[i]); // } int begin = 0, end = lenstr + 1; while (begin <= end) { int mid = (begin + end) >> 1; if (check(mid)) { begin = mid + 1; } else { end = mid - 1; } } cout << end << endl; // for (int i = ans[1]; i <= ans[1] + end - 1; ++i) { // printf("%c", str[i]); // } // cout << endl; return ; } int main() { #ifdef local freopen("data.txt","r",stdin); #endif int t; scanf("%d", &t); while (t--) { work(); } return 0; }
Codeforces Round #246 (Div. 2) D. Prefixes and Suffixes
http://codeforces.com/contest/432/problem/D
给定一个字符串,对于每一个prefix和suffix相等的,统计它们在整个串中出现的个数。
对于每一个prefix和suffix相等的情况,可以用kmp next[]加快速度
然后有多少个串出现在主串的话,
明显就是统计LCP(suffix(1)....)到所有后缀中,长度要>=当前前缀长度,这就是贡献。
dp预处理一下就行。
dp[i]表示suffix(1)和suffix(sa[i])的LCP
BOOK[i]表示>=i的个数

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 1e6 + 20; int sa[maxn], x[maxn], y[maxn], book[maxn]; //book[]大小起码是lenstr,book[rank[]] int subSa[13][10000 + 20]; bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] return r[a] == r[b] && r[a + len] == r[b + len]; } void da(char str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int RANK[maxn], height[maxn]; void CalcHight(char str[], int sa[], int lenstr) { for (int i = 1; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[] int k = 0; for (int i = 1; i <= lenstr - 1; ++i) { //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 k -= k > 0; int j = sa[RANK[i] - 1]; //排名在i前一位的那个串,相似度最高 while (str[j + k] == str[i + k]) ++k; height[RANK[i]] = k; } return ; } char str[maxn]; int tonext[maxn]; void get_next(char str[], int lenstr) { int i = 1, j = 0; tonext[1] = 0; while (i <= lenstr) { if (j == 0 || str[i] == str[j]) { tonext[++i] = ++j; } else j = tonext[j]; } return; } struct node { int len; LL val; bool operator < (const struct node & rhs) const { return len < rhs.len; } }ans[maxn]; int calc(int val, int lenstr) { int ans = 0; for (int i = 3; i <= lenstr + 1; ++i) { if (height[i] >= val) ans++; else return ans; } return ans; } int dp[maxn]; LL BOOK[maxn]; void init(int lenstr) { int x = RANK[1]; dp[x] = lenstr; for (int i = x + 1; i <= lenstr; ++i) { dp[i] = min(dp[i - 1], height[i]); } for (int i = x - 1; i >= 1; --i) { dp[i] = min(dp[i + 1], height[i + 1]); } for (int i = 1; i <= lenstr; ++i) { BOOK[dp[RANK[i]]]++; } for (int i = lenstr; i >= 1; --i) { BOOK[i] += BOOK[i + 1]; } return; } void work() { scanf("%s", str + 1); //cout << "0" << endl; exit(0); int lenstr = strlen(str + 1); str[lenstr + 1] = 0; str[lenstr + 2] = '�'; da(str, sa, lenstr + 1, 128); CalcHight(str, sa, lenstr + 1); init(lenstr); get_next(str, lenstr); int lenans = 0; ++lenans; ans[lenans].len = lenstr; ans[lenans].val = 1; int t = tonext[lenstr + 1]; while (t > 1) { int temp = t - 1; ++lenans; ans[lenans].len = temp; ans[lenans].val = BOOK[temp]; t = tonext[t]; } sort(ans + 1, ans + 1 + lenans); printf("%d ", lenans); for (int i = 1; i <= lenans; ++i) { printf("%d %I64d ", ans[i].len, ans[i].val); } // cout << dp[RANK[7]] << endl; return; } int main() { #ifdef local freopen("data.txt","r",stdin); //freopen("data2.txt", "w", stdout); long long int begin = clock(); #endif // for (int i = 1; i <= 1e4; ++i) { // printf("A"); // } work(); #ifdef local long long int end = clock(); cout << (end - begin) << endl; #endif return 0; }
来一题加强版的,数据范围达到1e6
http://acm.gdufe.edu.cn/Problem/read/id/1338
题意是一样的。但是我用后缀数组做居然超时了,我觉得复杂度应该是O(nlogn),可能评测机问题吧,也可能常数太大。一直过不了。还没学dc3,不知道dc3能否逆袭。(试了,DC3成功逆袭,不过不习惯字符串从0开始,)
既然不行,就考虑下dp吧。
用dp[i]表示str[1...i]这个前缀在整个串中出现的次数。
一开始所有dp值都应该是1,这个好理解,因为就是自己出现一次了嘛。
然后,先看这样一个问题,统计所有前缀在本串中出现的次数。就是先不管它是否和后缀匹配先。(这个用next数组记录一下马上出来。不成问题)
那么怎么统计所有前缀出现的次数呢?
枚举每一个next[i],dp[next[i] - 1] += dp[i - 1]
意思是:和当前位置前后缀相同的,可以加上我出现的次数。就是ABACABA这样,已经知道了ABACABA出现了一次,然后前后缀ABA和ABA重复出现,那么dp[3]肯定能够加上dp[7]的,dp[7]包含了dp[7]个"ABA",就这个意思。
一路dp下去。

1 #include <cstdio> 2 #include <cstdlib> 3 #include <cstring> 4 #include <cmath> 5 #include <algorithm> 6 using namespace std; 7 #define inf (0x3f3f3f3f) 8 typedef long long int LL; 9 10 #include <iostream> 11 #include <sstream> 12 #include <vector> 13 #include <set> 14 #include <map> 15 #include <queue> 16 #include <string> 17 const int maxn = 1e6 + 20; 18 int tonext[maxn]; 19 char str[maxn]; 20 int dp[maxn]; 21 void get_next(int lenstr) { 22 int i = 1, j = 0; 23 tonext[1] = 0; 24 while (i <= lenstr) { 25 if (j == 0 || str[i] == str[j]) { 26 tonext[++i] = ++j; 27 } else j = tonext[j]; 28 } 29 return; 30 } 31 struct node { 32 int len, val; 33 bool operator < (const struct node & rhs) const { 34 return len < rhs.len; 35 } 36 }ans[maxn]; 37 void work() { 38 scanf("%s", str + 1); 39 int lenstr = strlen(str + 1); 40 get_next(lenstr); 41 for (int i = 1; i <= lenstr + 1; ++i) dp[i] = 1; 42 for (int i = lenstr + 1; i >= 2; --i) { 43 int t = tonext[i] - 1; 44 dp[t] += dp[i - 1]; 45 } 46 // for (int i = 1; i <= lenstr; ++i) { 47 // cout << dp[i] << " "; 48 // } 49 // cout << endl; 50 int lenans = 0; 51 int t = lenstr + 1; 52 while (t > 1) { 53 int temp = t - 1; 54 ++lenans; 55 ans[lenans].len = temp; 56 ans[lenans].val = dp[temp]; 57 t = tonext[t]; 58 } 59 sort(ans + 1, ans + 1 + lenans); 60 printf("%d ", lenans); 61 for (int i = 1; i <= lenans; ++i) { 62 printf("%d %d ", ans[i].len, ans[i].val); 63 } 64 return; 65 } 66 int main() { 67 #ifdef local 68 freopen("data.txt","r",stdin); 69 #endif 70 work(); 71 return 0; 72 }

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 3 * 1000000 + 20; const int N = maxn; #define F(x) ((x)/3+((x)%3==1?0:tb)) #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) int r[maxn]; int wa[maxn],wb[maxn],wv[maxn],WS[maxn]; int sa[maxn]; int c0(int *r,int a,int b) { return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2]; } int c12(int k,int *r,int a,int b) { if(k==2) return r[a]<r[b]||r[a]==r[b]&&c12(1,r,a+1,b+1); else return r[a]<r[b]||r[a]==r[b]&&wv[a+1]<wv[b+1]; } void sort(int *r,int *a,int *b,int n,int m) { int i; for(i=0; i<n; i++) wv[i]=r[a[i]]; for(i=0; i<m; i++) WS[i]=0; for(i=0; i<n; i++) WS[wv[i]]++; for(i=1; i<m; i++) WS[i]+=WS[i-1]; for(i=n-1; i>=0; i--) b[--WS[wv[i]]]=a[i]; return; } void dc3(int *r,int *sa,int n,int m) { //涵义与DA 相同 int i,j,*rn=r+n,*san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p; r[n]=r[n+1]=0; for(i=0; i<n; i++) if(i%3!=0) wa[tbc++]=i; sort(r+2,wa,wb,tbc,m); sort(r+1,wb,wa,tbc,m); sort(r,wa,wb,tbc,m); for(p=1,rn[F(wb[0])]=0,i=1; i<tbc; i++) rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++; if(p<tbc) dc3(rn,san,tbc,p); else for(i=0; i<tbc; i++) san[rn[i]]=i; for(i=0; i<tbc; i++) if(san[i]<tb) wb[ta++]=san[i]*3; if(n%3==1) wb[ta++]=n-1; sort(r,wb,wa,ta,m); for(i=0; i<tbc; i++) wv[wb[i]=G(san[i])]=i; for(i=0,j=0,p=0; i<ta && j<tbc; p++) sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++]; for(; i<ta; p++) sa[p]=wa[i++]; for(; j<tbc; p++) sa[p]=wb[j++]; return; } int rank[maxn], height[maxn]; void calheight(int *r,int *sa,int n) { // 此处N为实际长度 int i,j,k=0; // height[]的合法范围为 1-N, 其中0是结尾加入的字符 for(i=1; i<=n; i++) rank[sa[i]]=i; // 根据SA求RANK for(i=0; i<n; height[rank[i++]] = k ) // 定义:h[i] = height[ rank[i] ] for(k?k--:0,j=sa[rank[i]-1]; r[i+k]==r[j+k]; k++); //根据 h[i] >= h[i-1]-1 来优化计算height过程 } char str[maxn]; int tonext[maxn]; void get_next(int lenstr) { int i = 0, j = -1; tonext[0] = -1; while (i < lenstr) { if (j == -1 || str[i] == str[j]) { tonext[++i] = ++j; } else j = tonext[j]; } return; } int dp[maxn]; int book[maxn]; void init(int lenstr) { int begin = rank[0]; dp[begin] = lenstr; for (int i = begin + 1; i <= lenstr; ++i) { dp[i] = min(dp[i - 1], height[i]); } for (int i = begin - 1; i >= 0; --i) { dp[i] = min(dp[i + 1], height[i + 1]); } // for (int i = 0; i < lenstr; ++i) { // printf("%d ", dp[rank[i]]); // } for (int i = 0; i < lenstr; ++i) book[dp[rank[i]]]++; for (int i = lenstr - 1; i >= 0; --i) { book[i] += book[i + 1]; } // for (int i = 0; i <= lenstr; ++i) { // printf("%d ", book[i]); // } } struct node { int lenstr; int val; }ans[maxn]; void work() { scanf("%s", str); int lenstr = strlen(str); for (int i = 0; i < lenstr; ++i) r[i] = str[i]; r[lenstr] = 0; dc3(r, sa, lenstr + 1, 128); calheight(r, sa, lenstr); get_next(lenstr); init(lenstr); // for (int i = 0; i < lenstr; ++i) { // printf("%d ", rank[i]); // } int t = tonext[lenstr]; int toans = 0; ++toans; ans[toans].lenstr = lenstr; ans[toans].val = 1; while (t != 0) { ++toans; ans[toans].lenstr = t; ans[toans].val = book[t]; t = tonext[t]; } printf("%d ", toans); for (int i = toans; i >= 1; --i) { printf("%d %d ", ans[i].lenstr, ans[i].val); } } int main() { #ifdef local freopen("data.txt","r",stdin); #endif work(); return 0; }
POJ 3581 Sequence
http://poj.org/problem?id=3581
给定一个数组,要求分成三组,每组倒序,然后合并成新的一组,要求字典序最小。
找到pos1, pos2这两个转折点进行倒序即可。
对于第一段,很容易找,直接把数组倒序一次(因为本来就要全部倒序的了,这样倒序求个sa[]就直接是输出答案中字典序最小)
求个sa,满足第一个sa[i]且sa[i] >= 2即可,因为起码要有3段,要保证一下。
对于第二段,有点小变化,考虑倒序后的序列,: 3、2、0、5、0、5
第二段应该是倒序0、5、0、5的,但是这样的sa会倒序最后的那个0、5
那么就是字典序第二小咯?也不是,2、3、0、5这样,就直接调换0、5可以了。
那么考虑在3、2、0、5、0、5后面加些东西,既不影响全局排名,又能使得选出正确答案。
开始的时候想在最后加个inf,这样排名就被影响了,而且前面些例子也能得到正确ans
但是,反例也是很多的,例如0、5、8、0、5、9、8、0、5 inf
你这样的话第二段就会选到加粗那些,这样是不对的,应该就选个0、5,然后第三段再倒序
例子就是:
12
8 4 -1 5 0 8 9 5 0 8 5 0
这就说明选第二段的时候同时还要兼顾第三段。。
因为剩下的那些数字,也就是第三段,开头是固定的了,就是a[]数组中最后的那个数字,那么就是说a[n]这个数字要影响第二段的选取,如果a[n]很少的,第二段选一个数字,这样第三段倒过来就会最小化。那么就考虑在剩下的数字末尾加上最后那个数字,去排名。
但是还是wa。原因很简单,上面那组例子都过不了,0、5、8、0、5、9、8、0、5 0,这样最会选出最后那个0,限制了一下还是错。
考虑会多个影响,就是不单指第一个数字影响,相同的时候,比较第二个数字,如果这样影响,那么就把这个段复制一次
eg: ABC复制成ABCABC,这样就什么影响都能考虑

#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <algorithm> using namespace std; #define inf (0x3f3f3f3f) typedef long long int LL; #include <iostream> #include <sstream> #include <vector> #include <set> #include <map> #include <queue> #include <string> const int maxn = 2 * 200000 + 20; int sa[maxn], x[maxn], y[maxn], book[maxn]; //book[]大小起码是lenstr,book[rank[]] bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] return r[a] == r[b] && r[a + len] == r[b + len]; } void da(int str[], int sa[], int lenstr, int mx) { int *fir = x, *sec = y, *ToChange; for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) { fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] book[str[i]]++; //统计不同字母的个数 } for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 //p是第二个关键字0的个数 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) p = 0; for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 for (int i = 1; i <= lenstr; ++i) if (sa[i] > j) //如果排名第i的起始位置在长度j之后 sec[++p] = sa[i] - j; //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 //sec[]保存的是下标,现在对第一个关键字排序 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; //因为sec[i]才是对应str[]的下标 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 ToChange = fir; fir = sec; sec = ToChange; fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 p = 2; for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; } return ; } int toHash[maxn]; int a[maxn]; int b[maxn]; int to; map<int, int> liu; void work() { int n; scanf("%d", &n); for (int i = 1; i <= n; ++i) { scanf("%d", &a[i]); b[i] = a[i]; } sort(b + 1, b + 1 + n); for (int i = 1; i <= n; ++i) { if (!liu[b[i]]) { ++to; liu[b[i]] = to; } } for (int i = 1; i <= n; ++i) { toHash[i] = liu[a[i]]; } // for (int i = 1; i <= n; ++i) { // cout << toHash[i] << " "; // } reverse(toHash + 1, toHash + 1 + n); reverse(a + 1, a + 1 + n); int pos1, pos2 = 0; toHash[n + 1] = 0; da(toHash, sa, n + 1, to); for (int i = 2; i <= n + 1; ++i) { if (sa[i] >= 3) { pos1 = sa[i]; for (int j = sa[i]; j <= n; ++j) { printf("%d ", a[j]); } break; } } // printf(" "); int nowlen = pos1 - 1; for (int i = 1; i <= nowlen; ++i) { toHash[i + nowlen] = toHash[i]; } nowlen *= 2; toHash[nowlen + 1] = 0; // toHash[nowlen + 1] = toHash[1]; // cout << toHash[1] << "fff" << endl; da(toHash, sa, nowlen + 1, to + 1); for (int i = 1; i <= nowlen + 1; ++i) { if (sa[i] >= 2 && sa[i] <= nowlen / 2) { for (int j = sa[i]; j <= nowlen / 2; ++j) { printf("%d ", a[j]); } pos2 = sa[i]; break; } } // cout << pos2 - 1 << "ff" << endl; // cout << pos2 << "***" << endl; for (int i = 1; i <= pos2 - 1; ++i) { printf("%d ", a[i]); } return; } int main() { #ifdef local freopen("data.txt","r",stdin); #endif work(); return 0; }
例如
10
8 4 -1 5 0 8 5 0 5 0
就要考虑全部,
其实讲白了,为什么要重复写一次,因为最后的ans绝对是重复写一次后的子串,用这样来做个sa[],输出的就必能保证最小
POJ 3415 Common Substrings
http://poj.org/problem?id=3415
后缀数组 + 单调栈
题目是给定两个串,要求找出两个串的公共子串并且公共子串的长度要大于等于K
首先总体上去看,肯定是枚举每一个A的后缀,然后再枚举每一个B的后缀,去比较这两个串的LCP,如果LCP >= K,那么对于答案的贡献就是LCP - K + 1;
然后直接枚举的话,枚举两个后缀的LCP可以用RMQ预处理O(1)得到,复杂度还是O(n^2)的,样例就是全部是aaaa的字符串然后K = 1;
那么考虑分类讨论,按照排名枚举,先枚举所有A,如果是A的后缀,则记录,然后没一个B的后缀,就去记录里面匹配一次,找出所有LCP >= k的,计算贡献。但很明显,如果一开始记录什么都没,然后先枚举了B的后缀,那么这部分是算漏了。那么容易想到再做一次,这次记录B的后缀,用A匹配,就行了。现在就是要高效地计算出这些数值。
注意到我们是按排名进行枚举,也就是从heigh[1] -- heigh[n],如果记录中的值是1、3、7、5、4的话,再枚举一个B进来,去枚举所有记录,LCP最大会是多少呢?ans是4,为什么呢?可以回顾下两个后缀LCP(suffix(i), suffix(j))是怎么计算的。相邻排名中的LCP就是这段height[]的最小值,1、3、7、5、4、B,加粗字体中的最小值是4,所以他们的LCP最多也只是4。故需要用单调栈来维护。加入5的时候,其实就可以把7去除了,但是7中也有长度为5的字符串,怎么办?cnt记录
对于每一个LCP,用一个单调递增的栈来记录下,记录的时候多记录一个值cnt表示这个LCP出现的次数。
这样枚举能达到O(n)的复杂度。

1 #include <cstdio> 2 #include <cstdlib> 3 #include <cstring> 4 #include <cmath> 5 #include <algorithm> 6 using namespace std; 7 #define inf (0x3f3f3f3f) 8 typedef long long int LL; 9 10 #include <iostream> 11 #include <sstream> 12 #include <vector> 13 #include <set> 14 #include <map> 15 #include <queue> 16 #include <string> 17 const int maxn = 2e5 + 20; 18 int sa[maxn], x[maxn], y[maxn], book[maxn]; //book[]大小起码是lenstr,book[rank[]] 19 bool cmp(int r[], int a, int b, int len) { //这个必须是int r[] 20 return r[a] == r[b] && r[a + len] == r[b + len]; 21 } 22 void da(char str[], int sa[], int lenstr, int mx) { 23 int *fir = x, *sec = y, *ToChange; 24 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 25 for (int i = 1; i <= lenstr; ++i) { 26 fir[i] = str[i]; //开始的rank数组,只保留相对大小即可,开始就是str[] 27 book[str[i]]++; //统计不同字母的个数 28 } 29 for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; //统计 <= 这个字母的有多少个元素 30 for (int i = lenstr; i >= 1; --i) sa[book[fir[i]]--] = i; 31 // <=str[i]这个字母的有x个,那么,排第x的就应该是这个i的位置了。 32 //倒过来排序,是为了确保相同字符的时候,前面的就先在前面出现。 33 //p是第二个关键字0的个数 34 for (int j = 1, p = 1; p <= lenstr; j <<= 1, mx = p) { //字符串长度为j的比较 35 //现在求第二个关键字,然后合并(合并的时候按第一关键字优先合并) 36 p = 0; 37 for (int i = lenstr - j + 1; i <= lenstr; ++i) sec[++p] = i; 38 //这些位置,再跳j格就是越界了的,所以第二关键字是0,排在前面 39 for (int i = 1; i <= lenstr; ++i) 40 if (sa[i] > j) //如果排名第i的起始位置在长度j之后 41 sec[++p] = sa[i] - j; 42 //减去这个长度j,表明第sa[i] - j这个位置的第二个是从sa[i]处拿的,排名靠前也//正常,因为sa[i]排名是递增的 43 //sec[]保存的是下标,现在对第一个关键字排序 44 for (int i = 0; i <= mx; ++i) book[i] = 0; //清0 45 for (int i = 1; i <= lenstr; ++i) book[fir[sec[i]]]++; 46 for (int i = 1; i <= mx; ++i) book[i] += book[i - 1]; 47 for (int i = lenstr; i >= 1; --i) sa[book[fir[sec[i]]]--] = sec[i]; 48 //因为sec[i]才是对应str[]的下标 49 //现在要把第二关键字的结果,合并到第一关键字那里。同时我需要用到第一关键//字保存的记录,所以用指针交换的方式达到快速交换数组中的值 50 ToChange = fir; 51 fir = sec; 52 sec = ToChange; 53 fir[sa[1]] = 0; //固定的是0 因为sa[1]固定是lenstr那个0 54 p = 2; 55 for (int i = 2; i <= lenstr; ++i) //fir是当前的rank值,sec是前一次的rank值 56 fir[sa[i]] = cmp(sec, sa[i - 1], sa[i], j) ? p - 1 : p++; 57 } 58 return ; 59 } 60 int rank[maxn]; 61 int height[maxn]; 62 void CalcHight(char str[], int sa[], int lenstr) { 63 for (int i = 1; i <= lenstr; ++i) rank[sa[i]] = i; //O(n)处理出rank[] 64 int k = 0; 65 for (int i = 1; i <= lenstr - 1; ++i) { 66 //最后一位不用算,最后一位排名一定是1,然后sa[0]就尴尬了 67 k -= k > 0; 68 int j = sa[rank[i] - 1]; //排名在i前一位的那个串,相似度最高 69 while (str[j + k] == str[i + k]) ++k; 70 height[rank[i]] = k; 71 } 72 return ; 73 } 74 int k; 75 char str[maxn]; 76 char sub[maxn]; 77 struct node { 78 int cnt; //记录长度为val的串有多少个 79 int val; //每个val只能在A或者B出现,不能同时出现 80 }stack[maxn]; 81 void work() { 82 cin >> str + 1; 83 cin >> sub + 1; 84 int lenstr = strlen(str + 1); 85 int newlen = lenstr; 86 int lensub = strlen(sub + 1); 87 str[++newlen] = '$'; 88 for (int i = 1; i <= lensub; ++i) { 89 str[++newlen] = sub[i]; 90 } 91 str[newlen + 1] = 0; 92 da(str, sa, newlen + 1, 128); 93 CalcHight(str, sa, newlen + 1); 94 LL ans = 0; 95 int top = 0; 96 LL tans = 0; 97 for (int i = 3; i <= newlen + 1; ++i) { 98 if (height[i] < k) { 99 top = tans = 0; 100 } else { 101 int cnt = 0; 102 // int mi = min(sa[i - 1], sa[i]); 103 // int mx = max(sa[i - 1], sa[i]); 104 int mi = sa[i - 1]; 105 int mx = sa[i]; 106 if (mi <= lenstr) { //val在A出现 107 tans += height[i] - k + 1; 108 cnt++; //在A中,长度为height[i]的出现一次 109 } 110 while (top >= 1 && height[i] <= stack[top].val) { 111 tans -= stack[top].cnt * (stack[top].val - height[i]); 112 cnt += stack[top].cnt; 113 --top; 114 } 115 if (mx > lenstr) ans += tans; 116 ++top; 117 stack[top].cnt = cnt; 118 stack[top].val = height[i]; 119 } 120 } 121 top = tans = 0; 122 for (int i = 3; i <= newlen + 1; ++i) { 123 if (height[i] < k) { 124 top = tans = 0; 125 } else { 126 int cnt = 0; 127 // int mi = min(sa[i - 1], sa[i]); 128 // int mx = max(sa[i - 1], sa[i]); 129 int mi = sa[i]; 130 int mx = sa[i - 1]; 131 if (mx > lenstr) { 132 cnt++; 133 tans += height[i] - k + 1; 134 } 135 while (top >= 1 && height[i] <= stack[top].val) { 136 tans -= stack[top].cnt * (stack[top].val - height[i]); 137 cnt += stack[top].cnt; 138 --top; 139 } 140 ++top; 141 stack[top].cnt = cnt; 142 stack[top].val = height[i]; 143 if (mi <= lenstr) ans += tans; 144 } 145 } 146 cout << ans << endl; 147 } 148 149 int main() { 150 #ifdef local 151 freopen("data.txt","r",stdin); 152 #endif 153 ios::sync_with_stdio(false); 154 while (cin >> k && k) work(); 155 return 0; 156 }
分享一篇学校后缀数组的博客,适合看题目,讲解还是挺少的
http://www.cnblogs.com/yefeng1627/archive/2013/08/02/3233611.html
