矩阵快速幂和矩阵乘法

矩阵并不是一个数而是可以表示一个比较复杂的模型（集合），而集合里封装着任意类型的值，而矩阵乘法则是一个比较重要的一个运算方式。

先说一下矩阵乘法的定义：

矩阵乘以矩阵的时候。

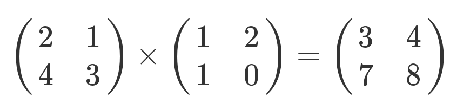
这个结果是怎么算出来的？

 

也就是说，结果矩阵第m行与第n列交叉位置的那个值，等于第一个矩阵第m行与第二个矩阵第n列，对应位置的每个值的乘积之和。

公式则是：其中c_ij为A的第i行与B的第j列对应乘积的和，即:

C_ij =Σa_ik*b_kj(1<=i<=n,1<=j<=n,1<=k<=n)。

Example(线性方程式)

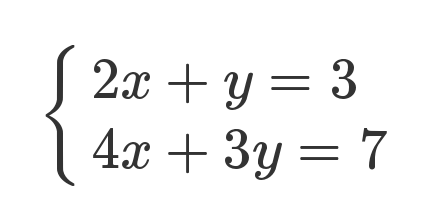
矩阵的最初目的，只是为线性方程组提供一个简写形式。

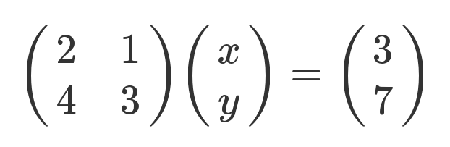
附矩阵乘法的代码

const int N=100;  
int c[N][N];  //c是最终的矩阵
void multi(int a[][N],int b[][N],int n)  
{  
    memset(c,0,sizeof c);  
    for(int i=1;i<=n;i++)  
        for(int j=1;j<=n;j++)  
        　　for(int k=1;k<=n;k++)  
        　　　　c[i][j]+=a[i][k]*b[k][j];  
} 

快速幂

求幂时我们常常会因结果太大而导致速度很慢，这时候我们就需要运用倍增的思想特殊的乘法应运而生————快速幂。

举个例子，如果求a₁₀，我们需要求十次，而如果我们用了快速幂就可以把a₁₀转变为二进制的形式从而加快运算速度。

而我们又知道aⁱ=(a^i/2)2

因此就有如下代码

总的来说就是把指数变小，底数变大，让运算次数变小的过程。（感觉我就这句话写的有用

int fastpow(int a,int i)
{
    int ans=1;//ans是最后的结果
    int res=a;//res就相当于上文中的a的i-1次方。
    while (i>0)
    {
        if (i%2==1)//因为当I是奇数的时候你就不能再把它分成2进制啦
            ans=ans*res;//这时候就将res乘上去
        res=res*res;//底数不停变大
        i=i/2;指数缩小
    }
    return ans;
}

接下来就是矩阵快速幂了。

根据以上赘述，如果一个数能快速幂。那么一个矩阵也能快速幂。

原因：只要满足结合律的数学运算就都可以使用快速幂

把快速幂与矩阵乘法相结合就是矩阵快速幂，其中快速幂的过程并不需要修改，只要定义一个关于矩阵的结构体并重载一下乘法运算符就可以了,为了方便运算，同时尽量满足矩阵乘法的性质，下面的矩阵都是n*n的。

这就是矩阵乘法代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
long long n,k;
const long long MOD=1000000007;
struct Matrix
{
  long long m[100][100];
};
Matrix A,E,ANS;
Matrix cheng(Matrix X,Matrix Y)
{
  Matrix C;
  for(long long i=1; i<=n; i++)
    for(long long j=1; j<=n; j++)
      {
        C.m[i][j]=0;
        for(long long l=1; l<=n; l++)
          C.m[i][j]=(C.m[i][j]+(X.m[i][l]*Y.m[l][j]))%MOD;
      }
  return C;
}
Matrix qsort(Matrix X,long long p)
{
  Matrix S=E;
  while(p)
    {
      if(p&1) S=cheng(S,X);
      X=cheng(X,X);
      p>>=1;
    }
  return S;
}
int main()
{
  scanf("%lld%lld",&n,&k);
  for(long long i=1; i<=n; i++)
    E.m[i][i]=1;
  for(long long i=1; i<=n; i++)
    for(long long j=1; j<=n; j++)
      scanf("%lld",&A.m[i][j]);
  ANS=qsort(A,k);
  for(long long i=1; i<=n; i++)
    {
      for(long long j=1; j<=n; j++)
        printf("%lld ",ANS.m[i][j]);
      puts("");
    }
  return 0;
}

这个有什么用呢，我们下面再说。

矩阵优化

利用矩阵，我们可以优化许多有关于递推和动态规划的问题。 我们先看一个简单的例子：斐波那契数列 我们知道斐波那契数列的递推式是

F[i]=F[i−1]+F[i−2]。

但是这样递推在i很大的时候效率不高，并且若不用滚动操作，空间消耗也很大。

所以我们可以转变为：

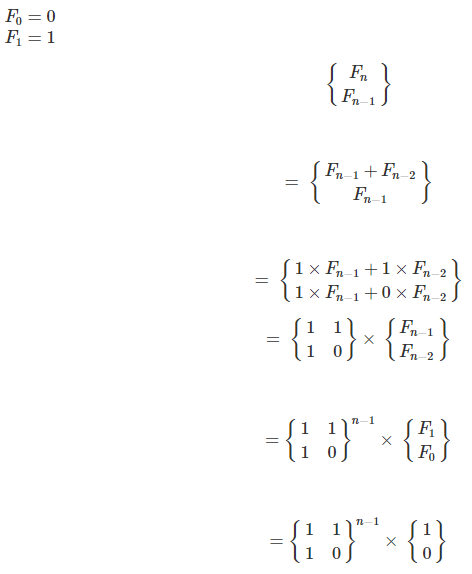
求F(n)等于求二阶矩阵的n - 1次方，结果取矩阵第一行第一列的元素。（因为要取矩阵的第一行才是Fn）。

问题转换为二阶矩阵的n次幂。

而计算二阶矩阵的N次幂运算，由于矩阵乘法满足结合律，这样，可以快速计算二阶矩阵的n次幂运算。