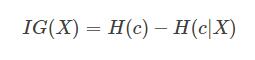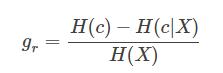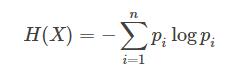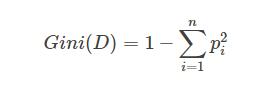决策树是通过一系列规则对数据进行分类的过程。它提供一种在什么条件下会得到什么值的类似规则的方法。
决策树分为分类树和回归树两种,分类树对离散变量做决策树,回归树对连续变量做决策树。
决策树学习
总思路
决策树学习的算法通常是一个递归地选择最优特征的过程
具体过程
- 开始:构建根结点,将所有训练数据都放在根结点。选择一个最优特征,按照这一特征将训练数据集分割成子集,使得各个子集有一个在当前条件下最好的分类。
- 然后递归向下处理子集
如果这些子集已经能够被基本正确分类,那么构建叶结点,并将这些子集分到所对应的叶结点中去;如果还有子集不能被基本正确分类,那么就对这些子集选择新的最优特征,继续对其进行分割,构建相应的结点。如此递归地进行下去,直至所有训练数据子集被基本正确分类,或者没有合适的特征为止。 - 最后每个子集都被分到叶结点上,即都有了明确的类。这就生成了一棵决策树
剪枝
决策树容易过拟合,一般来需要剪枝,缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。
特征选择
最优特征指的是对训练数据具有分类能力的特征。通常选择最优特征的准则是信息增益或信息增益比
1、信息增益
信息增益:特征X的信息而使得类Y的信息的不确定性减少的程度
信息增益 = entroy(前) - entroy(后)
2、信息增益比
(a)信息熵:平均而言发生一个事件的信息量大小。在数学上,信息熵其实是信息量的期望。
特征X的信息熵:
(b)Gini系数:表示数据的不纯度
在CART算法中, 基尼不纯度表示一个随机选中的样本在子集中被分错的可能性。