查找数组连成环形的和最大的连续子数组

设计思想：

　　把一个数组连成环，查找这个环的和最大的连续子数组时走到原来的数组尾部可以再继续加第一个元素，所以等价于构建一个原来数组2倍的数组

　　查找和最大的连续子数组方法：
设原先数组两倍的数组名为a,长度为2n - 1,原数组长度为n

　　　　定义一个当前的总和currectSum,初始值为a[0];定义一个当前总和的开始加和的位置下标currectStartIndex，初始值为0；定义一个记录连续加了多少个数的变量count，初始值为1。定义一个长度为3的结果数组result，用来存放最终找到的和最大的连续子数组的信息，result[0]记录开始下标，result[1]记录结束下标，result[2]记录总和，初始值为a[0]。
从数组a的第二个元素开始循环，循环到最后一个元素，每次循环中判断当前的总和currectSum是否小于或等于0，如果小于0那么应该舍弃前面的加和，重新开始加，从a[i]开始加，开始下标currectStartIndex记为i；如果currectSum大于0那么应继续加，加的元素的个数count++;然后比较当前总和跟result[2]的大小，如果当前总和currectSum大于result[2]，那么说明现在找到的子数组的和大于原先找到的子数组的和，应将当前的子数组的信息保存到结果数组信息中，即开始下标result[0] = currectStartIndex(当前的子数组的开始下标)，当前子数组的结束下标result[1] = i (当前遍历到的元素的下标)，当前子数组的和result[2] = currentSum(当前子数组的和)
然后判断子数组的元素个数count，如果count >= n 即子数组的个数已经等于原数组长度了，说明和最大的子数组即为原数组，此时应该结束循环，result数组记录的信息即为和最大的子数组的信息。

代码：

package zuoYe;

import java.util.Scanner;


public class MaxSubArray {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        
        
        //输入数据
        System.out.println("请输入数组长度");
        int n = scan.nextInt();
        int[] a = new int[n];
        
        System.out.println("请输入数组元素");
        for(int i = 0;i < n;i++)
        {
            a[i] = scan.nextInt();
        }
        scan.close();
        //计算此数组的和最大的连续子数组
        int[] result = maxSub(a,a.length);
        System.out.println("不连接成环的和最大的连续子数组：");
        for(int i = result[0];i <= result[1];i++)
        {
            System.out.print(a[i] + "	");
        }
        System.out.println("和为：" + result[2]);
    
    
        
        
        //将此数组连成一个环，再计算此数组的和最大的连续子数组
        //连成一个环即将数组后再接上此数组，但是数组的最后一个元素不用接，相当于计算接上之后的数组的和最大子数组
        int[] b = new int[2 * n - 1];
        for(int i = 0;i < n - 1;i++)
        {
            b[i] = a[i];
            b[n + i] = a[i];
        }
        b[n - 1] = a[n - 1];
        int[] result2 = maxSub(b,n);
        System.out.println("

将数组连成环后的和最大的连续子数组：");
        for(int i = result2[0];i <= result2[1];i++)
        {
            System.out.print(b[i] + "	");
        }
        System.out.println("和为：" + result2[2]);

        
    }
    
    
    
    
    //计算a数组的和最大的连续子数组(a数组为连成环后的等价数组，即原数组的二倍，n为原数组的长度)
    public static int[] maxSub(int[] a,int n)
    {
        int an = a.length;//连成环的等价数组的长度
        int currectSum = a[0];//记录当前累加和，初始值为a[0]
        int currectStartIndex = 0;//记录当前累加的起始下标，初始值为0
        int count = 1;//记录累加元素的个数，初始值为1
        int[] result = new int[3];//记录结果子数组的信息，
        result[0] = 0;//结果子数组的开始下标
        result[1] = 0;//结果子数组的结束下标
        result[2] = a[0];//结果子数组的和
        for(int i = 1;i < an;i++)//依次遍历a数组的每个元素
        {
            if(currectSum <= 0)//如果当前累加和不大于0，不大于0对后续的元素没有贡献，可以去掉了，所以应从a[i]处重新开始加
            {
                currectSum = a[i];//将当前累加和赋值为a[i]
                currectStartIndex = i;//将当前累加的开始下标赋值为i
                count = 1;//将累加元素的个数记为1
            }
            else//当前累加和大于0，则继续加a[i]
            {
                currectSum += a[i];
                count++;//当前累加元素的个数加一
            }
            if(currectSum > result[2])//如果当前累加和大于原结果数组的累加和result[2],则应该将结果子数组信息更新为当前子数组，因为当前子数组的累加和大于结果子数组的和
            {
                result[0] = currectStartIndex;//结果子数组的开始下标为当前子数组的开始下标
                result[1] = i;//结果子数组的结束下标赋值为i
                result[2] = currectSum;//结果子数组的累加和赋值为当前子数组的累加和
            }
            if(count >= n)//如果累加的元素个数等于原数组（未连成环的数组）的长度，则说明已经加了最多的元素，不能再加了，也就是说和最大的子数组即为原数组，应该结束循环
            {
                break;
            }
        }
        return result;
    }
    
    
    
}

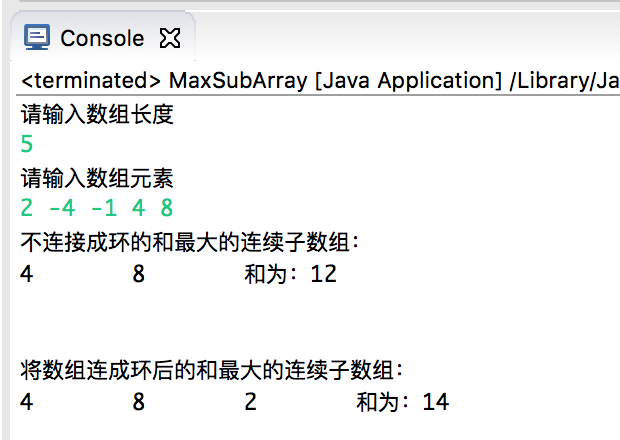
运行结果截图：