一、LDA算法
基本思想:LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
浅显来讲,LDA方法的考虑是,对于一个多类别的分类问题,想要把它们映射到一个低维空间,如一维空间从而达到降维的目的,我们希望映射之后的数据间,两个类别之间“离得越远”,且类别内的数据点之间“离得越近”,这样两个类别就越好区分。因此LDA方法分别计算“within-class”的分散程度Sw和“between-class”的分散程度Sb,而我们希望的是Sb/Sw越大越好,从而找到最合适的映射向量w。

LDA算法的主要优点有:
1)在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识。
2)LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优。
LDA算法的主要缺点有:
1)LDA不适合对非高斯分布样本进行降维,PCA也有这个问题。
2)LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
3)LDA在样本分类信息依赖方差而不是均值的时候,降维效果不好。
4)LDA可能过度拟合数据。
二、PCA算法
1、基本思想:
主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。
第一种解释是样本点到这个直线的距离足够近,第二种解释是样本点在这个直线上的投影能尽可能的分开。
我们知道“基于最小投影距离”就是样本点到这个超平面的距离足够近,也就是尽可能保留原数据的信息;而“基于最大投影方差”就是让样本点在这个超平面上的投影能尽可能的分开,也就是尽可能保留原数据之间的差异性。
假如我们把n'从1维推广到任意维,则我们的希望降维的标准为:样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。
基于上面的两种标准,我们可以得到PCA的两种等价推导。
2、优缺点
作为一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。
PCA算法的主要优点有:
1)仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
2)各主成分之间正交,可消除原始数据成分间的相互影响的因素。
3)计算方法简单,主要运算是特征值分解,易于实现。
4)当数据受到噪声影响时,最小的特征值所对应的特征向量往往与噪声有关,舍弃能在一定程度上起到降噪的效果。
PCA算法的主要缺点有:
1)主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。
2)方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。
为啥W'XX'W可以度量样本的差异性。最后得出结论:XX'就是X的协方差矩阵,其中对角线元素为各个字段的方差,而非对角线元素表示变量i和变量j两个字段的协方差。
注意:
由于 PCA 减小了特征维度,因而也有可能带来过拟合的问题。PCA 不是必须的,在机器学习中,一定谨记不要提前优化,只有当算法运行效率不尽如如人意时,再考虑使用 PCA 或者其他特征降维手段来提升训练速度。
降低特征维度不只能加速模型的训练速度,还能帮我们在低维空间分析数据,例如,一个在三维空间完成的聚类问题,我们可以通过 PCA 将特征降低到二维平面进行可视化分析。
3、算法流程
下面给出第一篇博文中总结的算法流程。
输入:n维样本集D=(x1,x2,...,xm)
输出:n'维样本集D'=(z1,z2,...,zm), 其中n'≤n
1. 对所有样本进行中心化(均值为0):这是必须

2. 计算样本的协方差矩阵XX'
3. 对协方差矩阵XX'进行特征分解(https://blog.csdn.net/jingyi130705008/article/details/78939463),得到对应的特征值和特征向量
4. 取出最大的n'个特征值对应的特征向量(w1,w2,...,wn'),对其进行标准化,组成特征向量矩阵W
5. 对于训练集中的每一个样本,进行相应转换:
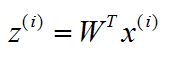
6. 得到输出样本集D'=(z1,z2,...,zm)
备注:有时候,我们不指定降维后的n'的值,而是换种方式,指定一个降维到的主成分比重阈值t。这个阈值t在(0,1]之间。假如我们的n个特征值为λ1≥λ2≥...≥λn,则n'可以通过下式得到:
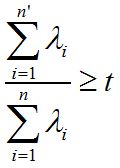
三、二者对比
LDA用于降维,和PCA有很多相同,也有很多不同的地方,因此值得好好的比较一下两者的降维异同点。
首先我们看看相同点:
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布。
我们接着看看不同点:
1)LDA是有监督的降维方法,而PCA是无监督的降维方法
2)LDA降维最多降到类别数k-1的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。