快速幂（fast power)

快速幂一种比较快速计算pow(a,b)的方法

其原理主要来自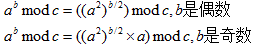

so,根据这个我们就可以依次迭代计算pow(a,b)

还有符合结合律的都可以使用快速幂，比如快速乘法————使用加法，等等

/*
    Name:
    Copyright:
    Author:  流照君
    Date: 2019/8/12 13:46:12
    Description:
*/
#include <iostream>
#include<string>
#include <algorithm>
#include <vector>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
ll pow(ll a,ll b,ll c)
{
    a=a%c;
    ll ans=1;
    while(b)
    {
        if(b&1)
        ans=ans*a%c;
        a=a*a%c;
        b=b/2;
    }
    return ans%c;
 } 
int main(int argc, char** argv)
{
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    ll a,b,c;
    cin>>a>>b>>c;
    printf("%lld^%lld mod %lld=",a,b,c);
    cout<<pow(a,b,c)<<endl;
    return 0;
}

至于取模因为取模在乘法中满足结合律 ，所以我们可以先取模再计算

题目https://www.luogu.org/problem/P1226

进阶还有矩阵快速幂，未完