【瞎口胡】Link-Cut Tree

Link Cut Tree 是一种神奇的数据结构。感觉完全不会，写下模板题的学习笔记。

LCT 中，比较重要的一点是将树边划分成实边和虚边。

对于每个非叶节点 (u)，我们选择一个儿子 (v) 作为 (u) 的实儿子。((u,v)) 是实边，(u) 到其它儿子的连边是虚边。

容易发现，实边组成了若干条实链，每个节点恰好在实链中出现了一次（链上只有一个节点仍然算作实链）。

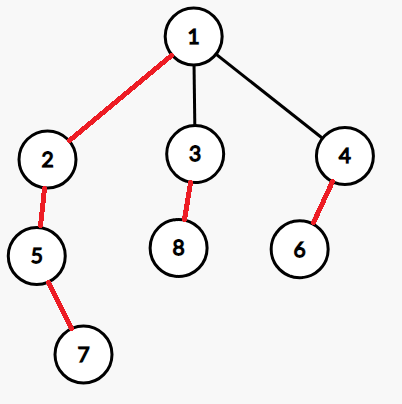
上图中，((1,2,5,7),(3,8),(4,6)) 是这棵树的实链。

对于每一条实链，我们用一棵 Splay 来维护节点。这棵 Splay 的中序遍历中，节点深度单调递增。

对于上图中的实链剖分，对应的 Splay 森林（注意形态可能不一样，但满足中序遍历节点深度单调递增）：

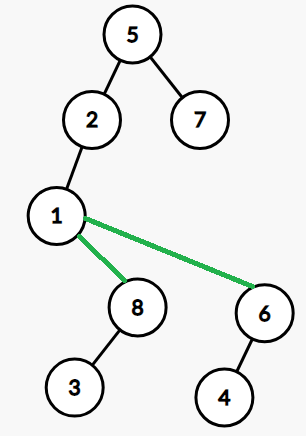
上图中绿色的边是虚边。

有一个显然的性质：如果 ((u,v)) 是实边且 (u) 的深度小于 (v)，那么 (v) 是 Splay 中 (u) 的儿子。无论 ((u,v)) 是否是实边，(v) 的父亲都指向 (u)。

Access ~ 点与根的连接

LCT 的核心操作是 access()。access(x) 改变了原树的实链剖分，同时构造出一棵中序遍历以根节点开始，以 (x) 结束的 Splay。

首先把 (x) 与 (x) 的实儿子的连边改成虚边，因为要构造的 Splay 中序遍历以 (x) 结束。然后不断地从深度较大的 Splay 跳到深度较小的 Splay，并把跳的过程中经过的所有虚边改为实边。

inline void access(int x){
	for(rr int y=0;x;y=x,x=fa(x)){
		splay(x),rc(x)=y,update(x);
	}
}

Makeroot ~ 换根

有了这个操作之后，我们可以来换根。makeroot(x) 的定义是让 (x) 成为原树的根。

我们怎么做呢？观察到，不在 (x) 到原来根路径上的点不会受到影响。于是我们只需要把 (x) 到原来根路径上的点拉出来，这就是 access(x)。然后我们将 (x) 旋转上去，这样 (x) 只有左子树（LCT 中 Splay 的性质：中序遍历节点深度单调递增）。我们想让 (x) 变成根，只需要翻转这棵 Splay。和做文艺平衡树时一样，打上翻转标记就行。

inline void rev(int x){
	if(!x)
		return;
	std::swap(lc(x),rc(x));
	tree[x].tag^=1;
	return;
}
inline void makeroot(int x){
	access(x),splay(x),rev(x);
	return;
}

Findroot ~ 找根

findroot(x) 的定义是找到 (x) 所在树的根。因为维护过程中可能会出现森林，于是这个函数对判断连通性很有帮助。

access(x) 之后再 splay(x)，按照上文，此时 (x) 只有左子树。往左子树一直走，就走到了根。

为了保证复杂度，找到原树的根之后要把根 splay() 成为 Splay 的根。

inline int findroot(int x){
	access(x),splay(x);
	while(lc(x))
		pushdown(x),x=lc(x); // 记得下放翻转标记
	splay(x);
	return x;
}

Split ~ 提取路径

split(x,y) 的定义是拉出 (x,y) 在原树上的路径成为一个 Splay。通常要保证 (x,y) 连通。

很简单，makeroot(x) 之后在 access(y) 即可。为了保证复杂度，需要 splay(y)。

inline void split(int x,int y){
	makeroot(x),access(y),splay(y);
	return;
}

Link ~ 连边

link(x,y) 的定义是连接 (x,y)。如果 (x,y) 已经连通，则无需连接。

也很简单，因为是无根树，所以我们并不在乎 (x) 和 (y) 的祖孙关系。默认 (x) 的父亲变成 (y)，makeroot(x) 再将 (x) 的父亲设为 (y) 就行。

如果 (x) 和 (y) 连通，那么 makeroot(x) 之后， findroot(y) 的结果一定为 (x)。特判即可。

inline void link(int x,int y){
	makeroot(x);
	if(findroot(y)==x){
		return;
	}
	fa(x)=y,update(y); // 记得 update
	return;
}

Cut ~ 断边

cut(x,y) 的定义是断掉 (x,y) 在原树上的边。如果没有边就不断。

首先用 findroot(y) 判掉 (x) 和 (y) 不连通的情况。接下来讨论 (x) 和 (y) 连通（即 findroot(y)==x）时：

findroot(y) 时已经执行了 access(y) 操作（见 findroot() 的实现），因此 (x) 到 (y) 的路径已经组成了一棵 Splay。此时若 (x,y) 之间有边，则：(x) 是 (y) 的父亲；(y) 没有左子树，否则这些点就会插在中序遍历中 (x) 和 (y) 的中间。

inline void cut(int x,int y){
	makeroot(x);
	if(findroot(y)==x&&fa(y)==x&&!lc(y)){
		rc(x)=fa(y)=0;
		update(x); // 记得 update
	}
	return;
}

模板题 Luogu P3690

题意

给定 (n) 个点以及每个点的权值，要你处理接下来的 (m) 个操作。

操作有四种，操作从 (0) 到 (3) 编号。点从 (1) 到 (n) 编号。

• 0 x y 代表询问从 (x) 到 (y) 的路径上的点的权值的 ( ext{xor}) 和。保证 (x) 到 (y) 是联通的。
• 1 x y 代表连接 (x) 到 (y)，若 (x) 到 (y) 已经联通则无需连接。
• 2 x y 代表删除边 ((x,y))，不保证边 ((x,y)) 存在。
• 3 x y 代表将点 (x) 上的权值变成 (y)。

(n,m leq 3 imes 10^5)，值域 (10^9)

题解

update(x) 改成维护异或和就好了。

询问操作就是 split 出来之后 Splay 上点 (y) 的异或和（因为我们 Splay 过）。

(1,2) 操作都是板子。(3) 操作的话需要先把 (x) splay 上去再修改，否则 (x) 在 Splay 上父亲的信息都没有得到更新。

# include <bits/stdc++.h>

const int N=100010,INF=0x3f3f3f3f;

struct Node{
	int son[2];
	int val,sum,tag,fa;
}tree[N];
int sta[N];
inline int read(void){
	int res,f=1;
	char c;
	while((c=getchar())<'0'||c>'9')
		if(c=='-')f=-1;
	res=c-48;
	while((c=getchar())>='0'&&c<='9')
		res=res*10+c-48;
	return res*f;
}
inline int& fa(int x){
	return tree[x].fa;
}
inline int& lc(int x){
	return tree[x].son[0];
}
inline int& rc(int x){
	return tree[x].son[1];
}
inline void update(int x){
	tree[x].sum=tree[lc(x)].sum^tree[rc(x)].sum^tree[x].val;
	return;
}
inline bool nroot(int x){
	return (lc(fa(x))==x)||(rc(fa(x))==x);
}
inline void rotate(int x){
	if(!nroot(x))
		return;
	int y=fa(x),z=fa(y),k=(rc(y)==x),ns=tree[x].son[!k];
	if(nroot(y))
		tree[z].son[rc(z)==y]=x;
	tree[x].son[!k]=y,tree[y].son[k]=ns;
	if(ns)
		fa(ns)=y;
	fa(y)=x,fa(x)=z;
	update(y),update(x); // 顺序注意 
	return;
}
inline void rev(int x){
	if(!x)
		return;
	std::swap(lc(x),rc(x));
	tree[x].tag^=1;
	return;
}
inline void pushdown(int x){
	if(!tree[x].tag)
		return;
	rev(lc(x)),rev(rc(x)),tree[x].tag=0;
	return;
}
inline void splay(int x){
	int top=0;
	int y=x;
	for(;;){ // 记得这里要先下放标记
		sta[++top]=y;
		if(!nroot(y))
			break;		
		y=fa(y);
	}
	while(top)
		pushdown(sta[top--]);
	while(nroot(x)){
		int y=fa(x),z=fa(y);
		if(nroot(y)){
			((rc(y)==x)==(rc(z)==y))?rotate(y):rotate(x);
		}
		rotate(x);
	}
	return;
}
inline void access(int x){
	for(int y=0;x;y=x,x=fa(x)){
		splay(x),rc(x)=y,update(x);
	}
	return;
}
inline void makeroot(int x){
	access(x),splay(x),rev(x);
	return;
}
inline int findroot(int x){
	access(x),splay(x);
	while(lc(x))
		pushdown(x),x=lc(x);
	splay(x);
	return x;
}
inline void split(int x,int y){
	makeroot(x),access(y),splay(y);
	return;
}
inline void link(int x,int y){
	makeroot(x);
	if(findroot(y)==x){
		return;
	}
	fa(x)=y,update(y);
	return;
}
inline void cut(int x,int y){
	makeroot(x);
	if(findroot(y)==x&&rc(x)==y&&!lc(y)){ // 顺序不能反 
		fa(y)=0,rc(x)=0;
		update(x);
	}
	return;
}
int main(void){
	int n=read(),m=read();
	for(int i=1;i<=n;++i){
		tree[i].sum=tree[i].val=read();
	}
	int x,y,opt;
	while(m--){
		opt=read(),x=read(),y=read();
		switch(opt){
			case 0:{
				split(x,y);
				printf("%d
",tree[y].sum);
				break;
			}
			case 1:{
				link(x,y);
				break;
			}
			case 2:{
				cut(x,y);
				break;
			}
			case 3:{
				splay(x),tree[x].val=y,update(x);
				break;
			}
		}
	}
	return 0;
}