hdu1542(求面积)
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1542
题意:对于每个矩形,给你左下和右上的坐标,求这些矩形的总覆盖面积。
思路:线段树+扫描线,由于给的矩形最多100个,但是坐标确特大,所以可以离散化我们要用来建树的坐标。
线段树:我们用它存两个值即可,一个是区间被覆盖长度,一个是当前是否还被覆盖。
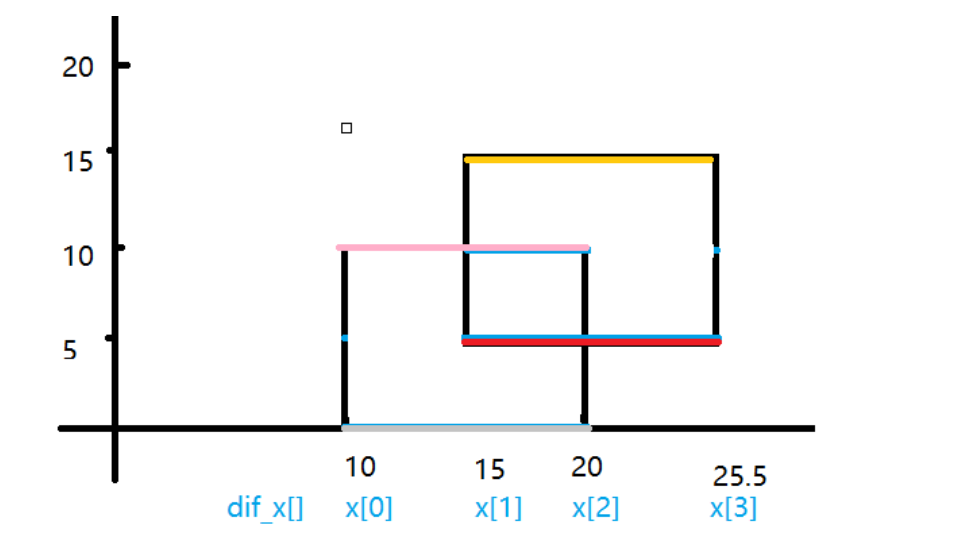
扫描线:我们可以把一幅图用一根长度为其在横坐标或者纵坐标投影的线去对其扫描一遍。
以横坐标为例:我们先把每个矩形拆分成两根与横坐标平行的线,并且记录他是矩形的上面的线还是下面的线,再对其进行按纵坐标高度排序,然后我们从最底的向上遍历每一条线,将当前遍历的线条的长度投影到线段树中(即对线段树中的【L,R】区间进行修改),对于是矩形下面的那根线我们就将改区间+1,反之-1,这样的话凡是区间值大于0的就是当前被覆盖的边长度了,我们只要用(覆盖总长度(即树根存储的那个覆盖长度值))* 高(即下一根线与这一根线的高度差)求和即是答案。
代码:

1 /**下面会有两个有问号的地方,我在这先解释一下,由于我们求的是线段长度,而我们建树是用点来建,就好比叶子,它只是一个点 , 2 因此我们要将其处理为树上的【l,r】区间 是点l到点r+1的长度,所以在树上更改len时是v【r+1】-v【l】(1),在插入线段时是【l,r-1】(2) 3 (当然,还有其他办法,比如建树时将区间改为[l,mid],[mid,r],再更新时用v【mid】和所要更新的线条的左右x值进行比较,但是我觉得这个比较好,因为它没有对线段树的操作模板改动太多) 4 **/ 5 #include<stdio.h> 6 #include<algorithm> 7 #include<vector> 8 #include<string.h> 9 using namespace std; 10 const int maxn = 110; 11 12 struct Tree{ 13 double len; 14 int flag; 15 }tree[maxn<<2]; 16 17 struct node{ 18 double l,r,h; 19 int flag; 20 friend bool operator < (node a,node b){ 21 return a.h<b.h; 22 } 23 }nd[maxn<<2]; 24 25 vector<double> v; 26 27 int getid(double val){//求取下标(离散化需用) 28 return lower_bound(v.begin(),v.end(),val)-v.begin(); 29 } 30 31 void Build(int k,int l,int r){ 32 tree[k].flag=0; 33 tree[k].len=0; 34 if(l==r) return ; 35 int mid=(l+r)>>1; 36 Build(k<<1,l,mid); 37 Build(k<<1|1,mid+1,r); 38 } 39 40 void change_len(int k,int l,int r){ 41 if(tree[k].flag){//如果这个区间被全部覆盖,则长度为l到r+1这两个点横坐标的差 42 tree[k].len=v[r+1]-v[l];//这里为什么要+1? (1) 43 }else if(l==r){//如果这是叶子节点,且没被完全覆盖(也就是没被覆盖),则长度为0 44 tree[k].len=0; 45 }else{//这是覆盖区间被分割的情况,要从它的左右儿子那里找覆盖长度 46 tree[k].len=tree[k<<1].len+tree[k<<1|1].len; 47 } 48 } 49 50 void update(int k,int l,int r,int L,int R,int flag){//flag可能是1或-1,1是下边,-1是上边 51 if(l>=L&&r<=R){ 52 tree[k].flag+=flag;// 对其覆盖进行修改 53 change_len(k,l,r);//更改区间覆盖长度 54 return ; 55 } 56 int mid=(l+r)>>1; 57 if(mid>=R){ 58 update(k<<1,l,mid,L,R,flag); 59 }else if(mid<L){ 60 update(k<<1|1,mid+1,r,L,R,flag); 61 }else{ 62 update(k<<1,l,mid,L,R,flag); 63 update(k<<1|1,mid+1,r,L,R,flag); 64 } 65 change_len(k,l,r);//同上 66 } 67 68 int N; 69 int main(){ 70 double x1,y1,x2,y2; 71 int Case=0; 72 while(~scanf("%d",&N)&&N){ 73 v.clear(); 74 memset(nd,0,sizeof(nd)); 75 int k=0; 76 double ans=0; 77 for(int i=0;i<N;i++){ 78 scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); 79 v.push_back(x1); 80 v.push_back(x2); 81 nd[k++]={x1,x2,y1,1};//存线条 82 nd[k++]={x1,x2,y2,-1}; 83 } 84 //离散化 85 sort(v.begin(),v.end()); 86 v.erase(unique(v.begin(),v.end()),v.end()); 87 88 sort(nd,nd+k); 89 int siz=v.size(); 90 91 Build(1,0,siz-1);//建一棵区间为【0,siz-1】的树 92 for(int i=0;i<k;i++){//遍历每一条线 93 update(1,0,siz-1,getid(nd[i].l),getid(nd[i].r)-1/*(2)*/,nd[i].flag);//这里为什么要减一? (2) 94 ans+=(nd[i+1].h-nd[i].h)*tree[1].len;//求答案 95 } 96 printf("Test case #%d ",++Case); 97 printf("Total explored area: %.2f ",ans); 98 } 99 return 0; 100 }
https://www.cnblogs.com/liwenchi/p/7259171.html(这是别人的博客,讲的挺好的)。
poj1177(求周长)
题目:http://poj.org/problem?id=1177
题意:给出坐标求周长
思路:这里比求面积要麻烦一点,但是代码都差不多,只要更改几个地方就好了。
求周长:对于扫描线运动的那一边的长度(下面默认为与x轴平行的),我们在进行扫描时从下向上扫描,我们每次求出的线段最大覆盖长度就会有重复,这要怎么解决呢?其实仔细观察会发现我们重复的就是上一次扫描时所计算出的len,所以减去它取绝对值就好了(为什么要绝对值?因为我们进行扫描时可能会出现当前的len比之前的小但是这其中又有我们要加入的长度(画个图手动扫一遍你就知道了));
与y轴平行的长度:我们可以再对y轴用一次扫描线,但是还有更简单的方法,那就是我们记录下当前覆盖长度有几段即可(num)(至于为什么,自己画个图也很容易看出来),让后用下一次要扫描的线段的高减去当前的*2*num即可,*2是因为矩形有两边,*num是因为扫描时可能不是连在一起的一段(见下图)。
至于num怎么求,我们需加个记录每个区间的左右端点是否被覆盖,这样我们就可以更新它的值了,如果整个区间被覆盖,则左右端点也会被覆盖,如果是有分割开覆盖的情况,则更新就是左儿子的num+又儿子的num再判断是否左儿子后端与右儿子前端是否可以被合并,是的话就减去1,否则不减。
代码:

1 #include<cstdio> 2 #include<vector> 3 #include<algorithm> 4 #include<string.h> 5 using namespace std; 6 const int maxn=5010; 7 8 int N; 9 vector<int> v; 10 struct node{ 11 int l,r,h,flag; 12 friend bool operator < (node a,node b){ 13 return a.h<b.h; 14 } 15 }nd[maxn*2]; 16 17 struct Tree{ 18 bool lc,rc;///线段左右端点石否被覆盖 19 int len; 20 int flag; 21 int num;///区间被几段线段覆盖 22 }tree[maxn<<2]; 23 24 int getid(int val){ 25 return lower_bound(v.begin(),v.end(),val)-v.begin(); 26 } 27 28 void Build(int k,int l,int r){ 29 tree[k].flag=tree[k].len=tree[k].lc=tree[k].rc=tree[k].num; 30 if(l==r) return ; 31 int mid=(l+r)>>1; 32 Build(k<<1,l,mid); 33 Build(k<<1|1,mid+1,r); 34 } 35 36 void change_len(int k,int l,int r){ 37 if(tree[k].flag){ 38 tree[k].len=v[r+1]-v[l]; 39 tree[k].lc=tree[k].rc=tree[k].num=1; 40 }else if(l==r){ 41 tree[k].lc=tree[k].rc=tree[k].num=tree[k].len=0; 42 }else{ 43 tree[k].len=tree[k<<1].len+tree[k<<1|1].len; 44 tree[k].lc=tree[k<<1].lc,tree[k].rc=tree[k<<1|1].rc;///左右端点是否被覆盖继承左儿子的左端点和右儿子的右端点 45 tree[k].num=tree[k<<1].num+tree[k<<1|1].num-(tree[k<<1].rc&tree[k<<1|1].lc);///上面有解释 46 } 47 } 48 49 void update(int k,int l,int r,int L,int R,int flag){ 50 if(l>=L&&r<=R){ 51 tree[k].flag+=flag; 52 change_len(k,l,r); 53 return ; 54 } 55 int mid=(l+r)>>1; 56 if(mid>=R){ 57 update(k<<1,l,mid,L,R,flag); 58 }else if(mid<L){ 59 update(k<<1|1,mid+1,r,L,R,flag); 60 }else{ 61 update(k<<1,l,mid,L,R,flag); 62 update(k<<1|1,mid+1,r,L,R,flag); 63 } 64 change_len(k,l,r); 65 } 66 67 int main(){ 68 int x1,y1,x2,y2; 69 while(scanf("%d",&N)!=EOF){ 70 int k=0; 71 int ans=0; 72 int last=0; 73 v.clear(); 74 memset(nd,0,sizeof(nd)); 75 for(int i=0;i<N;i++){ 76 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 77 v.push_back(x1); 78 v.push_back(x2); 79 nd[k++]={x1,x2,y1,1}; 80 nd[k++]={x1,x2,y2,-1}; 81 } 82 sort(nd,nd+k); 83 sort(v.begin(),v.end()); 84 v.erase(unique(v.begin(),v.end()),v.end()); 85 int siz=v.size()-1; 86 Build(1,0,siz); 87 for(int i=0;i<k;i++){ 88 update(1,0,siz,getid(nd[i].l),getid(nd[i].r)-1,nd[i].flag); 89 ans+=abs(tree[1].len-last)+(nd[i+1].h-nd[i].h)*2*tree[1].num; 90 last=tree[1].len; 91 } 92 printf("%d ",ans); 93 } 94 return 0; 95 }
hdu1255(计算被覆盖不止一次的面积)
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1255
第一个样例是答案7.62,不要被误解。
由于是计算不止被覆盖一次,所以要记录覆盖的情况,这里我们通过记录被覆盖>=1次和>=2次来计算,因为这样我们只要计算ans时用>=2的来计算就好了(至于为什么不用被覆盖1次和大于一次来记录,原因很简单,记录被覆盖1次的话更新操作会更加复杂(你要判断一条线段覆盖另一条时哪些是已经被覆盖,哪些是没有的,只有没有的才可加入被覆盖1次),而记录大于等于1就很好办了(详细的看代码吧)。
代码:

1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<vector> 5 #include<string.h> 6 using namespace std; 7 const int maxn=1010; 8 9 int N; 10 vector<double> v; 11 struct node{ 12 double l,r,h; 13 int flag; 14 friend bool operator < (node a,node b){ 15 return a.h<b.h; 16 } 17 }nd[maxn<<1]; 18 19 struct Tree{ 20 double len1,len2;///记录被覆盖次数大于等于1和大于等于2 21 int flag; 22 }tree[maxn<<3];///x坐标有2*maxn个所以要开8倍 23 24 int getid(double val){ 25 return lower_bound(v.begin(),v.end(),val)-v.begin(); 26 } 27 28 void Build(int k,int l,int r){ 29 tree[k].len1=tree[k].len2=tree[k].flag=0; 30 if(l==r) return ; 31 int mid=(l+r)>>1; 32 Build(k<<1,l,mid); 33 Build(k<<1|1,mid+1,r); 34 } 35 36 void change_len(int k,int l,int r){ 37 if(tree[k].flag>=2){///被覆盖大于两次,则改区间的len1,len2都为整个区间长度 38 tree[k].len1=tree[k].len2=v[r+1]-v[l]; 39 }else if(tree[k].flag==1){///被覆盖等于一次,则改区间的len1为整个区间长度,如果l!=r,则len2等于改节点左右儿子的len1和(因为改区间被完全覆盖了一次,那它儿子的区间可能有没被完全覆盖的len,而这些len就被覆盖了>=两次) 40 tree[k].len1=v[r+1]-v[l]; 41 if(l==r) tree[k].len2=0; 42 else tree[k].len2=tree[k<<1].len1+tree[k<<1|1].len1; 43 }else{///如果l!=r则继承他们儿子的len 44 if(l==r) tree[k].len1=tree[k].len2=0; 45 else{ 46 tree[k].len1=tree[k<<1].len1+tree[k<<1|1].len1; 47 tree[k].len2=tree[k<<1].len2+tree[k<<1|1].len2; 48 } 49 } 50 } 51 52 void update(int k,int l,int r,int L,int R,int flag){ 53 if(l>=L&&r<=R){ 54 tree[k].flag+=flag; 55 change_len(k,l,r); 56 return ; 57 } 58 int mid=(l+r)>>1; 59 if(mid>=R) update(k<<1,l,mid,L,R,flag); 60 else if(mid<L) update(k<<1|1,mid+1,r,L,R,flag); 61 else{ 62 update(k<<1,l,mid,L,R,flag); 63 update(k<<1|1,mid+1,r,L,R,flag); 64 } 65 change_len(k,l,r); 66 } 67 68 int main(){ 69 int T; 70 double x1,y1,x2,y2; 71 scanf("%d",&T); 72 while(T--){ 73 scanf("%d",&N); 74 v.clear(); 75 memset(nd,0,sizeof(nd)); 76 int k=0; 77 double ans=0; 78 for(int i=0;i<N;i++){ 79 scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); 80 v.push_back(x1); 81 v.push_back(x2); 82 nd[k++]={x1,x2,y1,1}; 83 nd[k++]={x1,x2,y2,-1}; 84 } 85 sort(nd,nd+k); 86 sort(v.begin(),v.end()); 87 v.erase(unique(v.begin(),v.end()),v.end()); 88 int siz=v.size()-1; 89 Build(1,0,siz); 90 for(int i=0;i<k;i++){ 91 update(1,0,siz,getid(nd[i].l),getid(nd[i].r)-1,nd[i].flag); 92 ans+=tree[1].len2*(nd[i+1].h-nd[i].h);///用len2去计算 93 } 94 printf("%.2lf ",ans); 95 } 96 return 0; 97 }
poj2528(离散化)
题目:http://poj.org/problem?id=2528
第一种写法:这题给出的数据很大,但数据量却不大,因此要离散化,可以通过一个lazy标记下放的操作求线段的覆盖情况(因为lazy如若存在值,则它下面的区间都要更改为该值,即相当于一个线段一般)。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<vector> 4 #include<algorithm> 5 #include<string.h> 6 using namespace std; 7 const int maxn=1e4+4; 8 int N; 9 vector<int> v; 10 bool vis[maxn<<1]; 11 struct node{ 12 int l,r; 13 }nd[maxn<<1]; 14 struct Tree{ 15 int lazy; 16 }tree[maxn*10]; 17 18 int getid(int val){ 19 return lower_bound(v.begin(),v.end(),val)-v.begin()+1; 20 } 21 22 void Build(int k,int l,int r){ 23 tree[k].lazy=0; 24 if(l==r) return ; 25 int mid=(l+r)>>1; 26 Build(k<<1,l,mid); 27 Build(k<<1|1,mid+1,r); 28 } 29 30 void pushdown(int k,int l,int r){ 31 if(l!=r&&tree[k].lazy){ 32 tree[k<<1].lazy=tree[k<<1|1].lazy=tree[k].lazy; 33 tree[k].lazy=0; 34 } 35 } 36 37 void update(int k,int l,int r,int L,int R,int cnt){ 38 if(l>=L&&r<=R){ 39 tree[k].lazy=cnt; 40 return ; 41 } 42 pushdown(k,l,r); 43 int mid=(l+r)>>1; 44 if(mid>=R) update(k<<1,l,mid,L,R,cnt); 45 else if(mid<L) update(k<<1|1,mid+1,r,L,R,cnt); 46 else{ 47 update(k<<1,l,mid,L,R,cnt); 48 update(k<<1|1,mid+1,r,L,R,cnt); 49 } 50 } 51 52 int ans; 53 54 void query(int k,int l,int r){ 55 if(tree[k].lazy){ 56 if(!vis[tree[k].lazy]){ 57 ans++; 58 vis[tree[k].lazy]=true; 59 } 60 return ; 61 } 62 if(l==r) return ; 63 int mid=(l+r)>>1; 64 query(k<<1,l,mid); 65 query(k<<1|1,mid+1,r); 66 } 67 68 int main(){ 69 int T,l,r; 70 scanf("%d",&T); 71 while(T--){ 72 int k=0; 73 memset(vis,false,sizeof(vis)); 74 memset(nd,0,sizeof(nd)); 75 v.clear(); 76 scanf("%d",&N); 77 for(int i=0;i<N;i++){ 78 scanf("%d%d",&l,&r); 79 v.push_back(l); 80 v.push_back(r); 81 nd[k++]={l,r}; 82 } 83 sort(v.begin(),v.end()); 84 v.erase(unique(v.begin(),v.end()),v.end()); 85 int siz=v.size(); 86 Build(1,1,siz); 87 for(int i=0;i<k;i++){ 88 update(1,1,siz,getid(nd[i].l),getid(nd[i].r),i+1); 89 } 90 ans=0; 91 query(1,1,siz); 92 printf("%d ",ans); 93 } 94 return 0; 95 }
第二种写法:由于它是求最后可以看到的海报有几张,所以我们可以倒着贴,然后用更新区间的方法判断当前贴入的海报是否已经被覆盖,如果当前贴的海报区间已经被完全覆盖,则这张海报看不见,反之可见。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<vector> 4 #include<algorithm> 5 #include<string.h> 6 using namespace std; 7 const int maxn=1e4+4; 8 int N; 9 vector<int> v; 10 bool vis[maxn<<4]; 11 struct node{ 12 int l,r; 13 }nd[maxn<<1]; 14 15 int getid(int val){ 16 return lower_bound(v.begin(),v.end(),val)-v.begin()+1; 17 } 18 19 void Build(int k,int l,int r){ 20 vis[k]=false; 21 if(l==r) return ; 22 int mid=(l+r)>>1; 23 Build(k<<1,l,mid); 24 Build(k<<1|1,mid+1,r); 25 } 26 27 bool update(int k,int l,int r,int L,int R,int cnt){ 28 if(vis[k]) return false;///当前查找区间已经全部被覆盖,则不必向下查找 29 if(l>=L&&r<=R){///查找到了可见区间 30 vis[k]=true; 31 return true; 32 } 33 bool flag; 34 int mid=(l+r)>>1; 35 if(mid>=R) flag=update(k<<1,l,mid,L,R,cnt); 36 else if(mid<L) flag=update(k<<1|1,mid+1,r,L,R,cnt); 37 else{///海报可能只有一部分看的见,所以分开查找 38 bool flag1=update(k<<1,l,mid,L,R,cnt); 39 bool flag2=update(k<<1|1,mid+1,r,L,R,cnt); 40 flag=flag1||flag2;///判断是否有可见 41 } 42 if(vis[k<<1]&&vis[k<<1|1]) vis[k]=true;///更行父节点(儿子都已经被覆盖,自然它也被覆盖) 43 return flag; 44 } 45 int main(){ 46 int T,l,r; 47 scanf("%d",&T); 48 while(T--){ 49 int k=0; 50 memset(nd,0,sizeof(nd)); 51 v.clear(); 52 scanf("%d",&N); 53 for(int i=0;i<N;i++){ 54 scanf("%d%d",&l,&r); 55 v.push_back(l); 56 v.push_back(r); 57 nd[k++]={l,r}; 58 } 59 sort(v.begin(),v.end()); 60 v.erase(unique(v.begin(),v.end()),v.end()); 61 int siz=v.size(); 62 Build(1,1,siz); 63 int ans=0; 64 for(int i=k-1;i>=0;i--){ 65 if(update(1,1,siz,getid(nd[i].l),getid(nd[i].r),i+1)){ 66 ans++; 67 } 68 } 69 printf("%d ",ans); 70 } 71 return 0; 72 }
理解有误的话,请指正!
