764. Largest Plus Sign

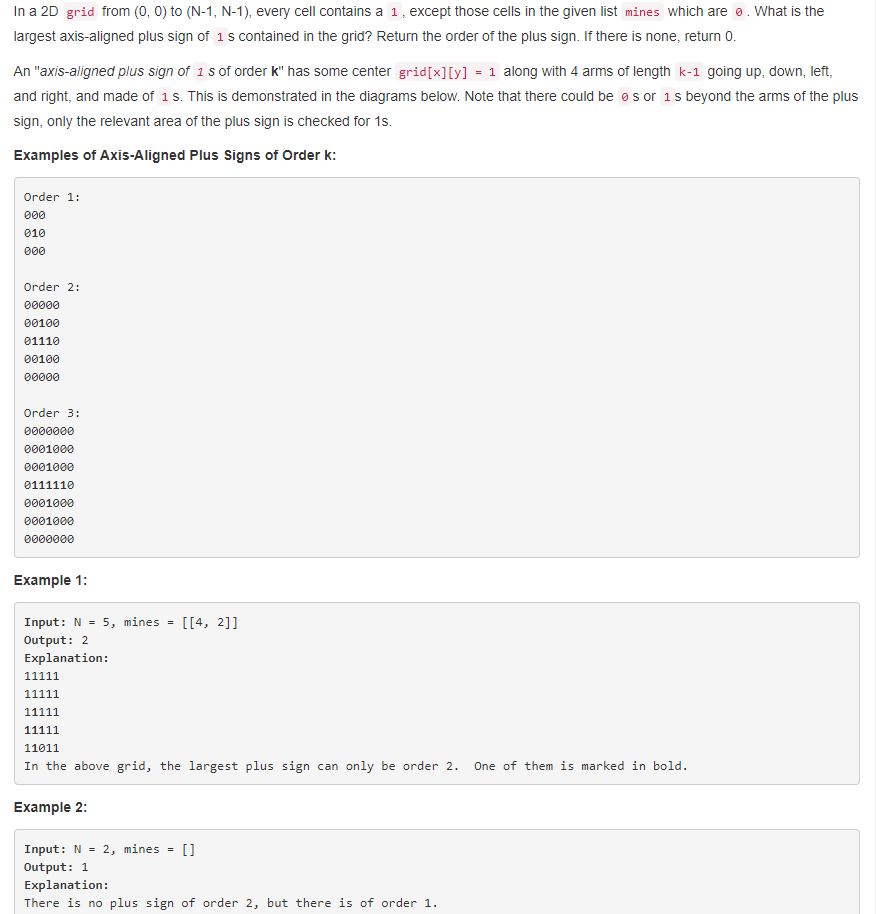
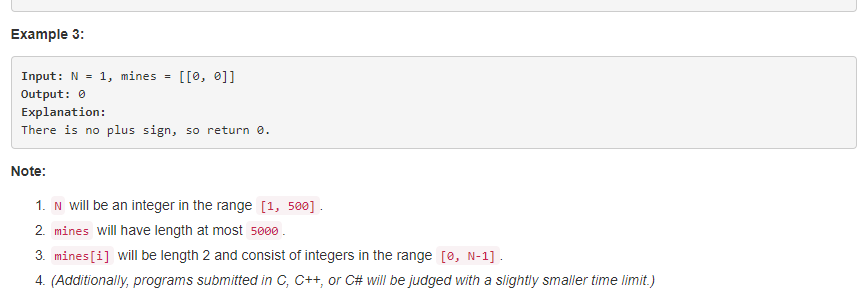
题目大意：

　　　　就是一个由1和0组成的正方形矩阵，求里面最大的加号的大小，这个大小就是长度。

　　　　

什么鬼啊，本来想自己想的，结果看了半天没看懂具体什么意思，然后查了下题解，希望有人说一下意思，结果一上来就是思路，还直接动态规划四个大字，我也是呵呵了

思路一：暴力Brute Force

　　　　就是用i, j 循环每一个位置，判断该位置的上下左右的最长“1序列”，复杂度大概是n³

　　　　***这个据说过不了

思路二：动态规划Dynamic Programming

　　　　说实话看完源码才想到的，感觉挺好的，直接看源码大把，很好理解，反正大概就是正向扫一遍，连续的1递增，比如0111011就是0123012，然后反向再扫一遍就是，取最小值。0121011

　　　　然后从上到下扫一遍，再从下到上扫一遍，同样取最小值

　　　　

class Solution {
public:
    int orderOfLargestPlusSign(int N, vector<vector<int>>& mines) {
        int map[505][505];
        memset(map,0,sizeof(map));
        for(int i=0;i<mines.size();i++)
        {
            map[mines[i][0]][mines[i][1]] = 1;
        }
        int dp[505][505];
        memset(dp,0,sizeof(dp));
        for(int i=0;i<N;i++) {
            int count = 0;
            for(int j=0;j<N;j++) {
                count = map[i][j]==0?++count:0;
                dp[i][j] = count;
            }
            
            count = 0;
            for(int j=N-1;j>=0;j--) {
                count = map[i][j]==0?++count:0;
                dp[i][j] = min(count, dp[i][j]);
            }
        }

        for(int i=0;i<N;i++) {
            int count = 0;
            for(int j=0;j<N;j++) {
                count = map[j][i]==0?++count:0;
                dp[j][i] = min(count, dp[i][j]);
            }
            
            count = 0;
            for(int j=N-1;j>=0;j--) {
                count = map[j][i]==0?++count:0;
                dp[j][i] = min(count, dp[i][j]);
            }
        }
        int ans = 0;
        for(int i=0;i<N;i++) {
            for(int j=0;j<N;j++) {
                ans = max(ans, dp[i][j]);
            }
        }
    }
};

思路三：二分

　　　　这个我也没有试，和暴力有点像，连续的1最大是N个，那么就找N/2长度的试，如果找到了就更长的，反正这样我猜复杂度应该是n²logn ?

　　　　有兴趣的试试吧