最短路径问题是 动态规划的一个实例。
1.最短路径问题的描述

2.举个例子来说明:
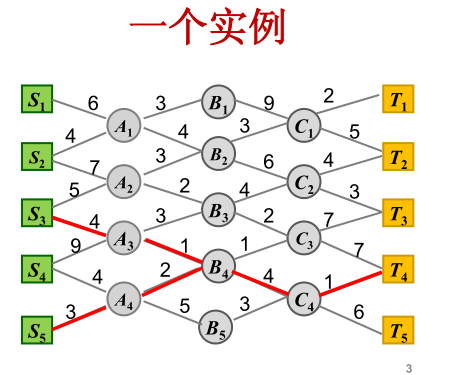
求从 S 到 T 的最短路径。
3.思考方式

4.利用动态规划求解问题
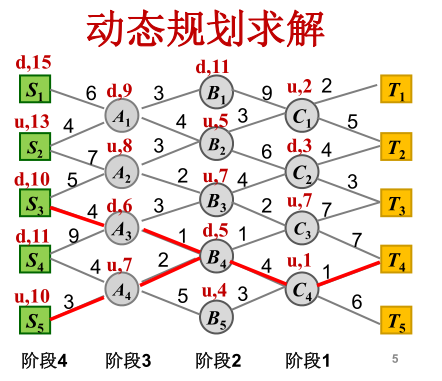
依次 考虑从 C 到 T 的最短距离。
考虑从 B 到 C 的最短距离
考虑从 A 到 B 的最短距离
考虑从 T 到 A 的最短距离
每次都是最短距离。
在整个过程中,我们把 我们的目标问题转化成了一个个的子问题,在子问题 求 最小值,最后解决了这个问题。
4.子问题的界定
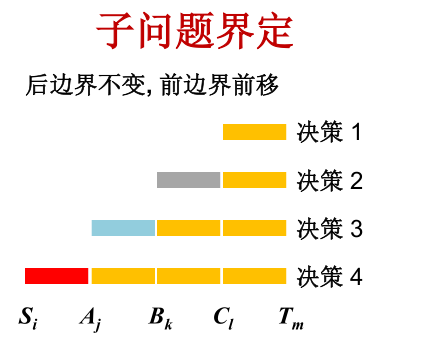
5.最短路程之间的依赖关系

每一次计算的时候都是依据前一个子问题。不需要一个一个计算。每次计算都可以直接利用前一个问题的解。
6.子问题的优化原则

6.利用动态规划求解是需要条件的,一个反例告诉你,动态规划求解的条件
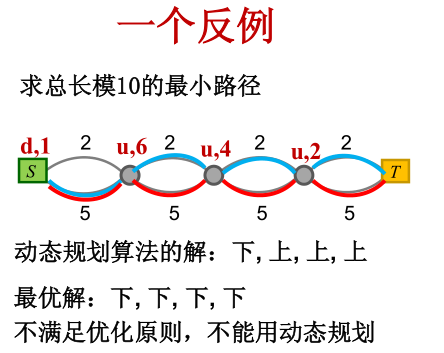
分析: 假如从S 到 T 经过的节点依次是 A B C ,从C 到 T ,模10,我们选择 上面的2 . 从 B 到 C,我们的两条路分别是 4 和 7 ,模10,我们选择 上面的 4 ,那么,从B到T的最短距离就是 6; 从 A 到 B ,我们的两条路分别是 6 和 9,模10,我们选择上面的路。
从 S 到 A ,两条路分别是 8 和 11, 此时 ,模10,我们选择下面的 路。这时,路径就如上图中蓝色的路径了。
但是,这是最优的路径吗?显然不是,红色的路线才是最优的路径。因为模10后,得到的结果为0,比 1 小。
为什么是错误的?
因为 破坏了动态规划的优化原则,它的问题和它的子问题的优化函数之间没有依赖关系。比如,我们考虑最后一段 即 C 到 T的距离,
显然, 2是最优解,而不是 5 。因此,破坏了优化原则的问题不能使用 动态规划。
7.动态规划 小结

可以用于求解组合优化问题。注意 动态规划的 最优化的原则。
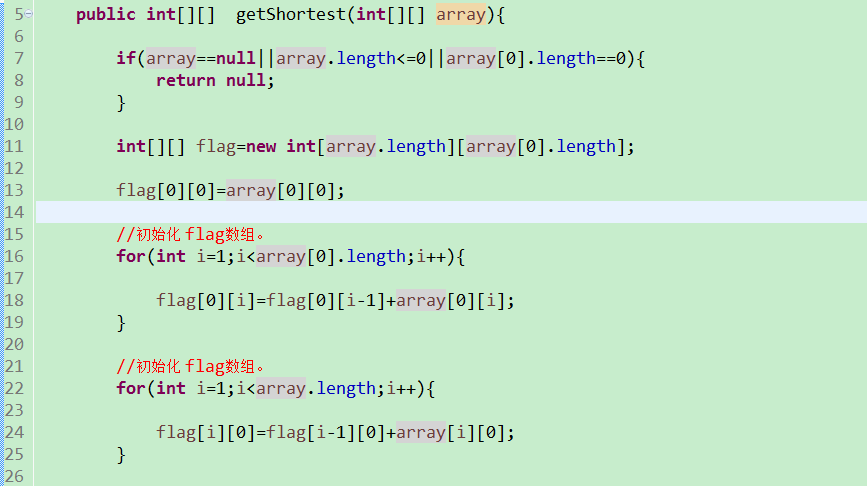
8.代码
这个问题的简化版本,编码实现:从矩阵的(0,0)位置到矩阵的(array.length-1,array[0].length-1)的位置的最小值。