牛客算法周周练9 A--符合条件的整数

地址：https://ac.nowcoder.com/acm/contest/5902/A

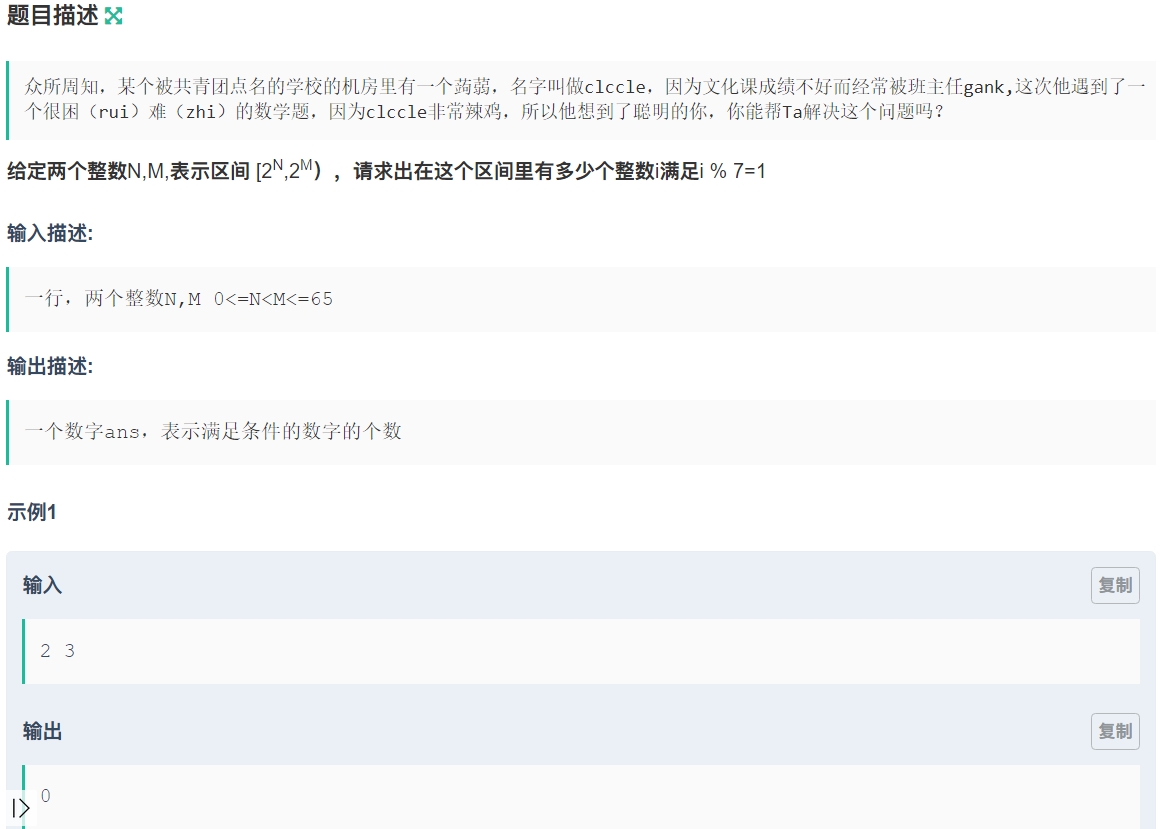
 解析：

2^65是可以用pow直接算的，这点不用担心

对于[L,R）的数目，可以由[1,R)-[1,L]来求出。

列举一下，可以发现，如果一个数x%7==1，那么它就是第(x/7)+1个。

所以我们只要找到最后一个小于等于L符合%7==1的数md1，以及最后一个小于R的符合%7==1的数md2，求出它们所在的位置，一减，就是答案

特别的，md1==pow(2,n)的时候，需要特殊处理一下

#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int maxn=1e3+10;
int s1[maxn],s0[maxn];
int main()
{
    int n,m;
    cin>>n>>m;
    ll m1=pow(2,n),m2=pow(2,m);
    ll md1,md2;
    for(ll i=m1;i>=1;i--)
    {
        if(i%7==1)
        {
            md1=i;break;
        }
    }
    for(ll i = m2-1;i>=1;i--)
    {
        if(i%7==1)
        {
            md2=i;break;
        }
    }
    ll s1,s2;
    s1=(md1)/7+1;
    s2=(md2)/7+1;
    if(md1==pow(2,n))
        cout<<s2-s1+1<<endl;
    else
        cout<<s2-s1<<endl;
}