poj 1106(半圆围绕圆心旋转能够覆盖平面内最多的点)

Transmitters

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4955		Accepted: 2624

Description

In a wireless network with multiple transmitters sending on the same frequencies, it is often a requirement that signals don't overlap, or at least that they don't conflict. One way of accomplishing this is to restrict a transmitter's coverage area. This problem uses a shielded transmitter that only broadcasts in a semicircle.

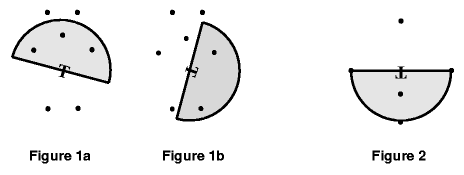
A transmitter T is located somewhere on a 1,000 square meter grid. It broadcasts in a semicircular area of radius r. The transmitter may be rotated any amount, but not moved. Given N points anywhere on the grid, compute the maximum number of points that can be simultaneously reached by the transmitter's signal. Figure 1 shows the same data points with two different transmitter rotations.

All input coordinates are integers (0-1000). The radius is a positive real number greater than 0. Points on the boundary of a semicircle are considered within that semicircle. There are 1-150 unique points to examine per transmitter. No points are at the same location as the transmitter.

Input

Input consists of information for one or more independent transmitter problems. Each problem begins with one line containing the (x,y) coordinates of the transmitter followed by the broadcast radius, r. The next line contains the number of points N on the grid, followed by N sets of (x,y) coordinates, one set per line. The end of the input is signalled by a line with a negative radius; the (x,y) values will be present but indeterminate. Figures 1 and 2 represent the data in the first two example data sets below, though they are on different scales. Figures 1a and 2 show transmitter rotations that result in maximal coverage.

Output

For each transmitter, the output contains a single line with the maximum number of points that can be contained in some semicircle.

Sample Input

25 25 3.5
7
25 28
23 27
27 27
24 23
26 23
24 29
26 29
350 200 2.0
5
350 202
350 199
350 198
348 200
352 200
995 995 10.0
4
1000 1000
999 998
990 992
1000 999
100 100 -2.5

Sample Output

3
4
4

题意：半圆围绕圆心旋转能够覆盖平面内最多的点
题解：先去掉所有和圆心距离大于r的点,然后我们以每一点和圆心组成的线段为边界来计算线段两边的点,比较出最大值就好了.记得赋值最大值的时候要赋值为0，因为它有可能不会进循环。

#include<stdio.h>
#include<iostream>
#include<string.h>
#include <stdlib.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int N = 160;
const double eps = 1e-8;
struct Point{
    double x,y;
}p[N],circle;
struct Line{
    Point a,b;
}line;
double r;
int n;
int cross(Point a,Point b,Point c){
    double ans = (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);
    if(fabs(ans)<eps) return 0;
    if(ans<0) return 1;
    return -1;
}
int main(){
    while(true){
        scanf("%lf%lf%lf",&circle.x,&circle.y,&r);
        if(r<=0) break;
        scanf("%d",&n);
        int k = 0;
        for(int i=0;i<n;i++){
            double x,y;
            scanf("%lf%lf",&x,&y);
            if((x-circle.x)*(x-circle.x)+(y-circle.y)*(y-circle.y)>r*r) continue;
            p[k].x = x;
            p[k++].y = y;
         }
         int temp1 ,temp2,mx = 0; ///mx要赋值为0，因为有可能一个点都没有,习惯赋值成-1被坑了一把
         for(int i=0;i<k;i++){
            line.a = p[i];
            line.b = circle;
            temp1=temp2 =0;
            for(int j=0;j<k;j++){
                if(cross(p[j],line.a,line.b)==0) {
                    temp1++;
                    temp2++;
                }else if(cross(p[j],line.a,line.b)==1){
                    temp1++;
                }else temp2++;
            }
            int ans = max(temp1,temp2);
            mx = max(ans,mx);
         }
         printf("%d
",mx);
    }
    return 0;
}