Minimal Ratio Tree
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3899 Accepted Submission(s): 1196
Problem Description
For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.
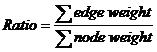
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Input
Input
contains multiple test cases. The first line of each test case contains
two integers n (2<=n<=15) and m (2<=m<=n), which stands for
the number of nodes in the graph and the number of nodes in the minimal
ratio tree. Two zeros end the input. The next line contains n numbers
which stand for the weight of each node. The following n lines contain a
diagonally symmetrical n×n connectivity matrix with each element shows
the weight of the edge connecting one node with another. Of course, the
diagonal will be all 0, since there is no edge connecting a node with
itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
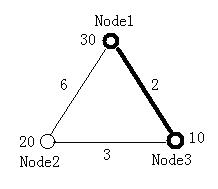
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output
For
each test case output one line contains a sequence of the m nodes which
constructs the minimal ratio tree. Nodes should be arranged in
ascending order. If there are several such sequences, pick the one which
has the smallest node number; if there's a tie, look at the second
smallest node number, etc. Please note that the nodes are numbered from 1
.
Sample Input
3 2
30 20 10
0 6 2
6 0 3
2 3 0
2 2
1 1
0 2
2 0
0 0
Sample Output
1 3
1 2
题意:在n个点中选m个点出来,求使上面的公式最小的m个点的组合。
题解:点比较少,状压31MS。。先用状态压缩选择m个点出来,然后再对选出来的点进行公式的计算。
#include <stdio.h> #include <iostream> #include <string.h> #include <algorithm> #include <math.h> using namespace std; const int N = 16; const int INF = 9999999999; int graph[N][N]; int weight[N]; int state[1<<N]; int a[N],result[N];; int n,m; int vis[N],low[N]; void input(){ for(int i=1;i<=n;i++) scanf("%d",&weight[i]); for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ scanf("%d",&graph[i][j]); } } } bool check(int num){ int cnt =0; while(num){ if(num&1) cnt++; num = num>>1; } if(cnt==m) return true; return false; } void init(int &k){ for(int i=0;i<(1<<n);i++){ if(check(i)) state[k++]=i; } k--; } int prim(int n,int pos){ memset(vis,0,sizeof(vis)); for(int i=0;i<n;i++){ low[a[i]] = graph[pos][a[i]]; } vis[pos] = true; int cost = 0; for(int i=1;i<n;i++){ int Min = INF; for(int j=0;j<n;j++){ if(!vis[a[j]]&&low[a[j]]<Min){ pos = a[j]; Min = low[a[j]]; } } vis[pos] = true; cost +=Min; for(int j=0;j<n;j++){ if(!vis[a[j]]&&low[a[j]]>graph[pos][a[j]]) low[a[j]] = graph[pos][a[j]]; } } return cost; } int main() { while(scanf("%d%d",&n,&m)!=EOF,n+m){ int k=0; init(k); int min_id=N; double _ratio = INF*1.0; input(); for(int i=0;i<=k;i++){ int num = state[i]; int t =0,V=0; for(int j=0;j<n;j++){ if((num>>j)&1){ ///这里代表第j+1个点要选进去 a[t++] = j+1; V += weight[j+1]; } } int cost = prim(t,a[0]); double temp1 = cost*1.0/V; if(temp1<_ratio){ _ratio = temp1; for(int i=0;i<t;i++) result[i] = a[i]; } } for(int i=0;i<m-1;i++){ printf("%d ",result[i]); } printf("%d ",result[m-1]); } }