逻辑回归

1. 线性回归： 是预测模型，关键是要建立回归方程（自变量和因变量的函数关系）。这样就可以通过回归方程，每输入一个X的值，就能预测Y的值是多少。

2.逻辑回归（Logistic Regression）： 是分类模型，是用于解决二分类（0 or 1）问题的机器学习方法，用于估计某种事物的可能性。是建立在线性回归的基础上。是将线性回归输出的Y值的范围压制在0-1之间，它是将线性回归所产生的值带入逻辑方程式，以将输出值压制在0-1之间。用来预测自变量X要分类到哪一类。通常因变量是二值变量0或者1，表示事件发生或不发生。

3.线性回归有很多相同之处，去除Sigmoid映射函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

Sigmoid函数，也称为逻辑函数（Logistic function）：

其函数曲线如下：

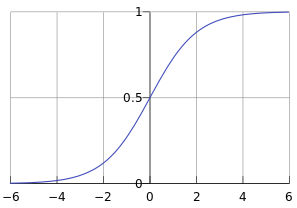
从上图可以看到sigmoid函数是一个s形的曲线，它的取值在[0, 1]之间，在远离0的地方函数的值会很快接近0或者1。它的这个特性对于解决二分类问题十分重要。

线性回归问题中的假设函数，而想要其输出值满足 ，引进Sigmod函数，如下所示：


的函数图像如下所示，由函数图像可知，sigmod函数能够满足逻辑回归的基本要求，并且当时可将其近似认为,而当时，认为，的输出，在某种程度上表示一个分类问题在给定x的条件下等于0或者1的概率。

4.逻辑回归的核心思想步骤：

　　（1） 先利用训练集建立回归方程：a₀+a₁x1+a₂x2+...+a_kx_k

　　（2）再将a₀+a₁x1+a₂x2+...+a_kx_k算出来的最终z值带入到逻辑函数中。

　　（3）如果g(z)大于0.5，则预测结果为1，否则为0.

　　

　　注意：

1. 因为g(z)算出来的是一个0-1之间的概率值，假设此概率值为p。则p=1/(1+e^-z)。则利用此等式，可以求出来Z值，两边取log以e为底的对数，可以得到：z=In(p/(1-p))。 其中，p/(1-p)代表胜算比（Odds Ratio）。In(p/(1-p)) = In(胜算比)。
2. 所以，逻辑回归就是试图找一条线性回归方程式来预测In(胜算比) 。
3. 因此，重要，逻辑回归模型为：In(p/1-p)=a₀+a₁x1+a₂x2+...+a_kx_k .其中，p为因变量Y=1的概率，x1,x2,...xk 为自变量，a0,a1,a2....ak为回归系数，可以通过数据进行估计得到。
4. 因此逻辑回归是估计某一事件发生的概率。逻辑回归构成预测变量z=In(p/(1-p)) 和 解释变量的线性函数。
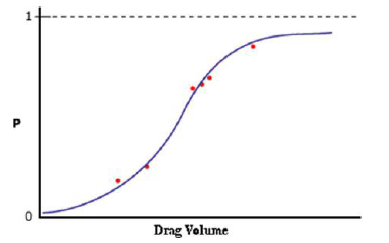
5. 预测变量通过逻辑函数转换成概率(p=1/(1+e^-z))，函数曲线形如S，横坐标为预测变量Z的值，也就是a₀+a₁x1+a₂x2+...+a_kx_k 算出来的值。纵坐标为概率值P，也就是把a₀+a₁x1+a₂x2+...+a_kx_k 算出来的z值带入到Sigmoid函数（Logistic function）：算出来的值p。