一、损失函数:是一种衡量损失和错误程度的函数
二、梯度下降法:是一种迭代的优化算法
梯度:是一个向量,表示一个函数在该点处,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值.
梯度下降法(Gradient Descent,GD)算法是求解最优化问题最简单、最直接的方法。梯度下降法是一种迭代的优化算法,对于优化问题:minf(w)
其基本步骤为:
- 随机选择一个初始点w0
- 重复以下过程:
- 决定下降的方向:di=−∂f(w)|wi/∂w
- 选择步长ρ
- 更新:wi+1=wi+ρ⋅di
- 决定下降的方向:di=−∂f(w)|wi/∂w
- 直到满足终止条件
三、sigmoid函数
Sigmoid函数是一个有着优美S形曲线的数学函数,在逻辑回归、人工神经网络中有着广泛的应用。Sigmoid函数的数学形式是: f(x)=1/(1+e−x) 它的导数可以用自身来表示:
f'(x)=f(x)(1-f(x))
函数连续,光滑,严格单调,以(0,0.5)中心对称,函数的取值在0-1之间,并且越靠近x=0的取值斜率越大,是一个非常良好的阈值函数。
sigmoid函数拥有良好的性质,可以用在分类问题上,如作为逻辑回归模型的分类器。
机器学习中一个重要的预测模型逻辑回归(LR)就是基于Sigmoid函数实现的。LR模型的主要任务是给定一些历史的{X,Y},其中X是样本n个特征值,Y的取值是{0,1}代表正例与负例,通过对这些历史样本的学习,从而得到一个数学模型,给定一个新的X,能够预测出Y。LR模型是一个二分类模型,即对于一个X,预测其发生或不发生。但事实上,对于一个事件发生的情况,往往不能得到100%的预测,因此LR可以得到一个事件发生的可能性,超过50%则认为事件发生,低于50%则认为事件不发生
从LR的目的上来看,在选择函数时,有两个条件是必须要满足的:
1. 取值范围在0~1之间。
2. 对于一个事件发生情况,50%是其结果的分水岭,选择函数应该在0.5中心对称。
从这两个条件来看,Sigmoid很好的符合了LR的需求。
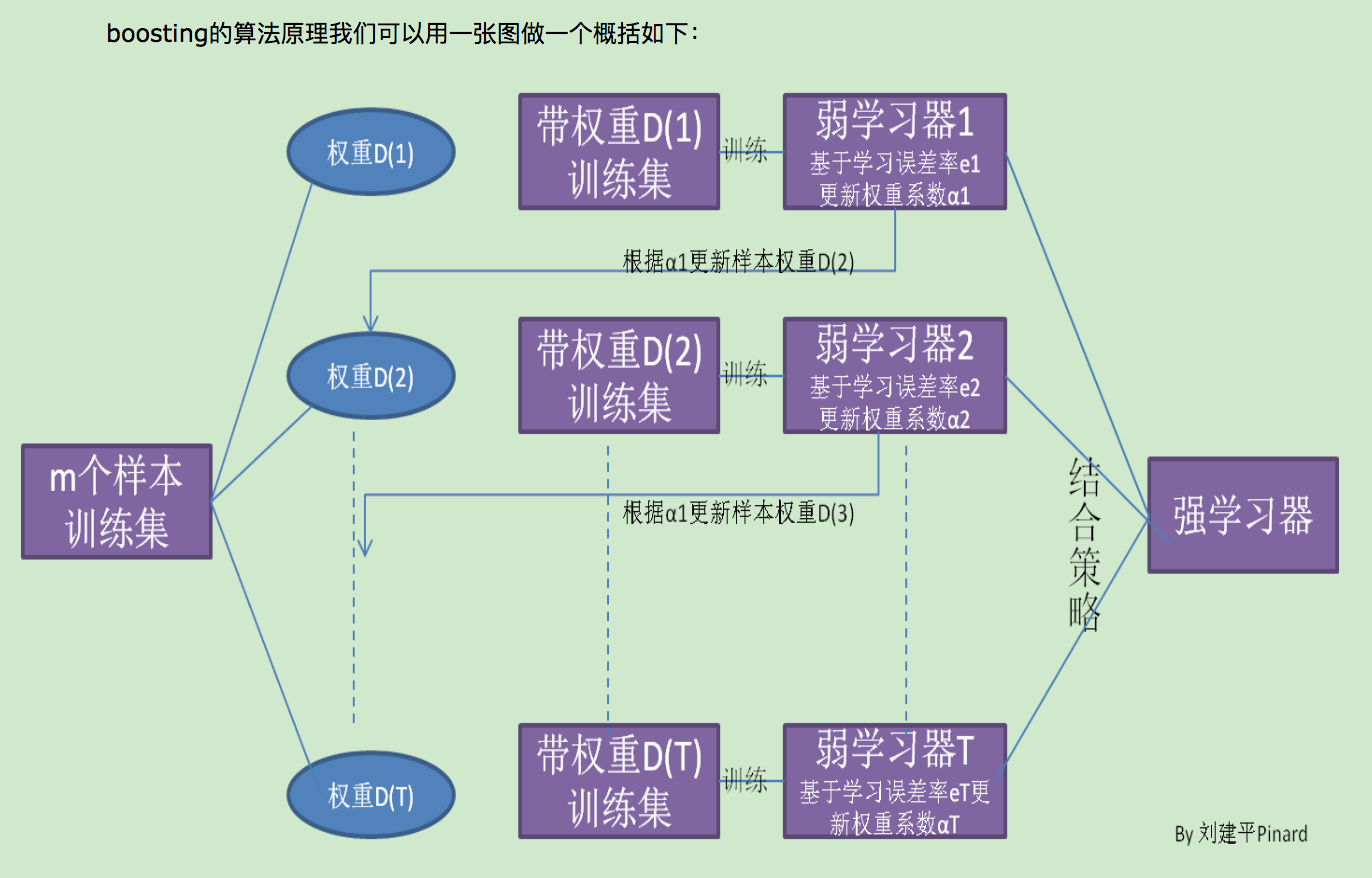
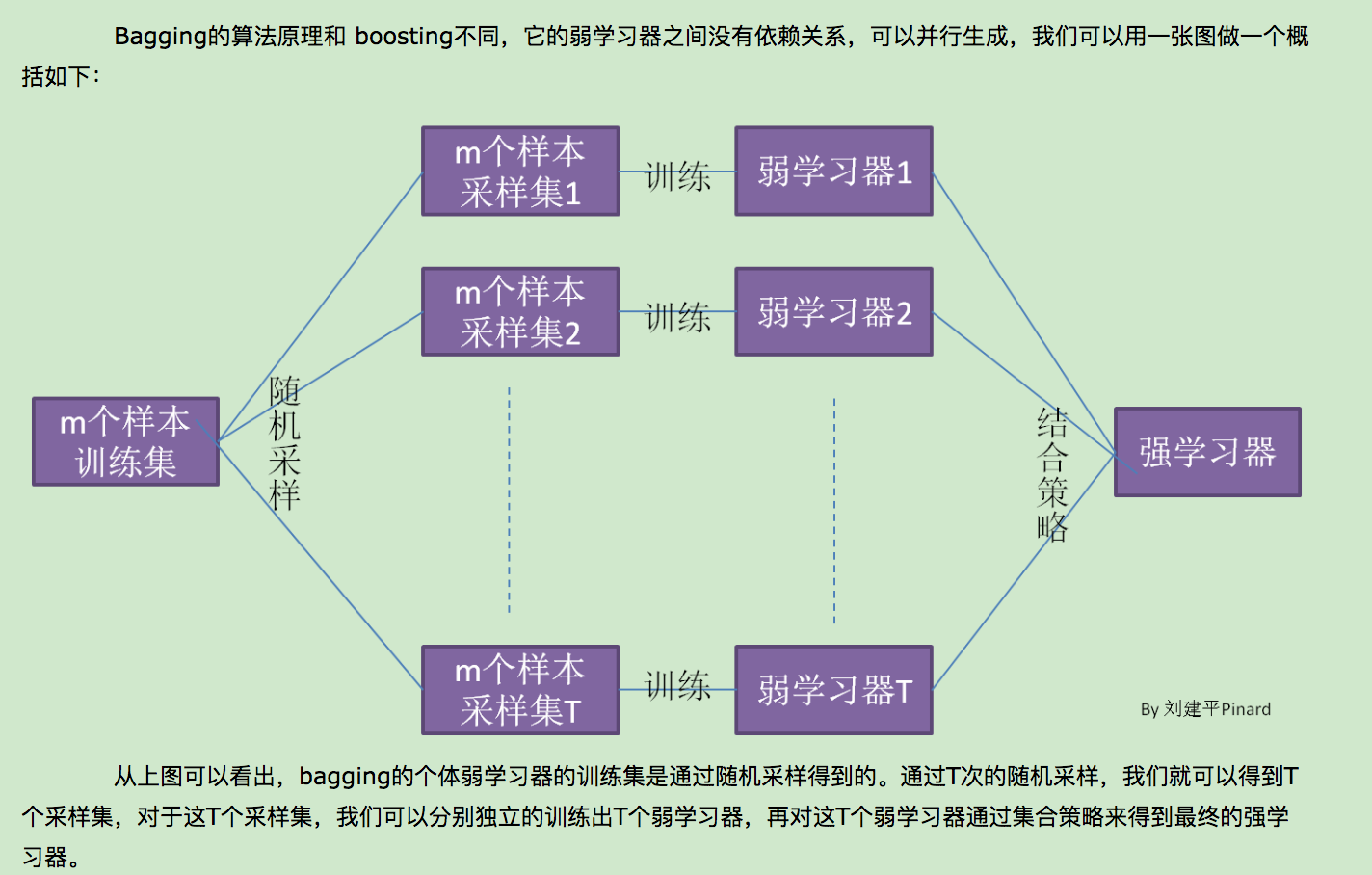
四、集成学习:它本身不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务。目前来说,同质个体学习器的应用是最广泛的,一般我们常说的集成学习的方法都是指的同质个体学习器。而同质个体学习器使用最多的模型是CART决策树和神经网络。同质个体学习器按照个体学习器之间是否存在依赖关系可以分为两类,第一个是个体学习器之间存在强依赖关系,一系列个体学习器基本都需要串行生成,代表算法是boosting系列算法,第二个是个体学习器之间不存在强依赖关系,一系列个体学习器可以并行生成,代表算法是bagging和随机森林(Random Forest)系列算法。