Octree
(by J. Eder 9225396) What is an Octree?
Using an Octree
Types of Octrees
What does it represent?
How is it managed?
How to structure Octree-structures
Pointerless full Octree
Traditional design of Pointer Octrees
Branch-On-Need-Octree
What is an Octree ?
(First I have to say, that it was discussed, if an Octree which doesn't branchs in all directions in the same moment is not an Octree: this paper doesn't matter when to branch, it just assumes that you have not less than zero and not more than eight child-nodes and in any meaning its matter is volumes)Because many volume data-sets are very large it isn’t possible to interactively render such a scene. The implementation of hierarchical data structures could make this better. An Octree is such a hierarchical data structure.
It is a kind of a tree, which nodes (except the leaves) each has max. eight child-nodes. Mostly the nodes represent volume-pieces which are further divided into max. eight “Octants” which are represented by the child-nodes. The Octants mostly are regular, but also irregular shapes are imaginable. If the maximum resolution is reached at one node, it’s a leave of the tree. If the leaves of a node have exactly the same attributes, it is possible to reduce them to a node. This is called condensation.
Using an octree
Usually an Octree represents a volume, but of course it is possible to use it for different applications, such as to represent spatial relationships of geometrical objects. But the most common use is to represent a volume. Some calculations work very much faster if they can be performed on condensed node. Of course each node "carries" a type of information in it. If its job is just to represent if the "voxel" is there or not it's a boolean data type. On the other hand it is arguable to store a complete set of values, for instance dense values, temperature values and the further. This data type is non boolean.Type of Octrees
There are several methods to distinguish the "family" of octrees, but I would say the best are: What does it represent?
How is it managed?
What does it represent?
There you can distinguish two mainly different types of information: Boolean and Non-Boolean Information. At the boolean information there's just the information saved, if the volume is interesting (BLACK) or not (WHITE). This binary decision only works clear for leaves, but for any ancestor-nodes there can be a third possibility: Some of the nodes could be BLACK and some of the nodes could be WHITE, then these ancestor-nodes are called "GRAY".With Non-Boolean data it's not so easy: The information can be any value and its the more unlikely that you can condense the nodes than the more possibilities the attributes of the nodes have to get set. Therefore mostly all ancestor-nodes are gray nodes, which means that cannot be condensed and for nearly all discrete volume points you need its ancestors, which need also memory. This can be enhanced until about the double amount.
How is it managed?
There are any positibilities to implement an octree, the mostly common approaches are pointer based and with array (pointerless). The pointerbased octrees have for each child node a pointer which shows the position of the child. Sometimes there is also a pointer to the ancestor. (Of course not to forget the attributes of the node) If a gray node is defined it means, that all pointers are filled and this of course takes memory. The next approach is the linear octree which works (nearly) without pointers. If you decide, always to make a "full" octree (all ancestors have all child-nodes), you exactly know for a given size of a volume the amount of nodes in one hierarchical plane. Thats why it's directly possible to calculate the address of the wanted node. This method is very memory effortable, because it assumes a full octree.If the path is saved, how to get from the root to the leaf, it needs not a full octree. Each node now possess' a key which describes to take which turn-off. These keys can be accessed through an array or a Hash-table.
How to structure Octree-structures
If you are working with trees it's hard enough to remember the correct pointer for the wanted child and not to accidentally exchange it. But with octrees is really tricky. That's why we should consider a name-giving convention. It's called the ZYX-convention. In this convention you take the binary number of 0-7 to describe the nodes. Then you say: first bit=Z-Coordinate, second bit is Y-Coordinate, third bit is X-Coordinate. For each of these coordinates you say "less" half or "greater" half (in coordinate direction) and for less you say 0 and for greater you say 1.Pointerless full Octree
In a full Octree each node has exactly eight children for each ancestor. Therefore you can directly calculate the total number of nodes.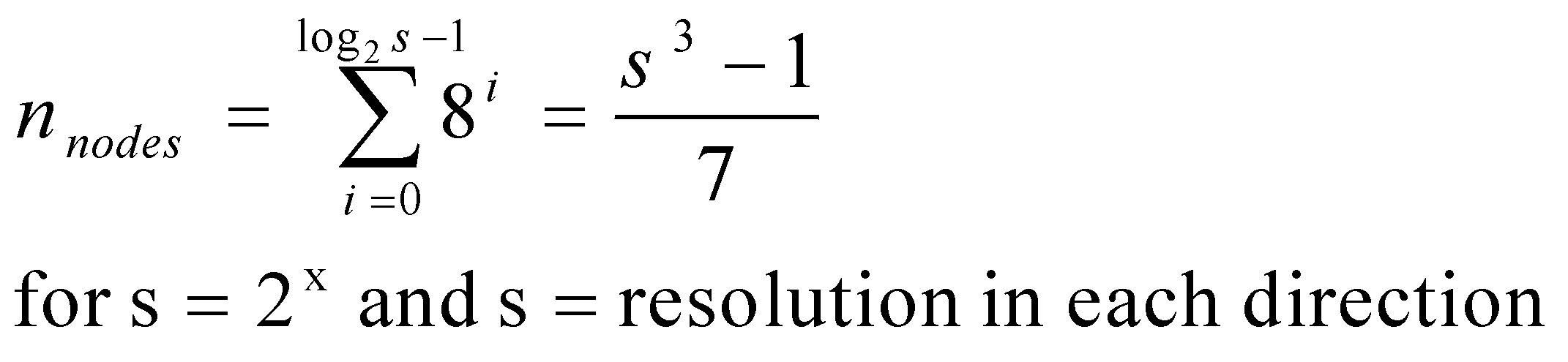
It is a regular structure and therefore the adress of the node can be directly calculated. It cost much memory ( for 320x320x40 you need about 40 Mill words) and therefore the traditional design is with pointers.
Traditional design of Pointer Octrees
Each ancestor-node has eight pointers which can be empty or can point to the child-node. It works with the "even-subdivision strategy". This means, that each range is devided in nearly similar parts and the child nodes nearly exactly describe the same volume. But the disadvantage is described below with an example of 16x8x4 :|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Branch-on-Need Octree
The basic idea is, that the tree is only branching if "necessary" trying branching similar to the power of 2. This is realized by dividing at that moment at the binary number of the range is losing its leftmost bit. That works like following: You write down the binary numbers of the ranges which are the differences of their "upper" and their "lower" limits. Then you write all leading zeros you need that you have the same number of digits of all dimensions. You now only branch in that dimensions which have a "1" in their leftmost bit. For example you have (16/15/8) or (10000/01111/01000): It is branching only in the X direction. You can determin the childs ranges just for the "upper" by simply removing the leftmost 1. It results in 0000, which means "no further branch". The "lower" child you just take as "1"s in the number of the number of digits of the remaining "upper" range. The "lower" child has 1111 which means it now is a "power"-node which means it branches in that dimension down for all nodes (like the power of 2: 15-7-3-1).(Source: ACM Transactions on Graphical, Vol.11 No3,July '92) //------------------------
|
OCTREE 教程 |
||||||||
对OCTREE的描述 OCTREE 是对3D空间进行划分,也可以叫空间分割。他允许你只对你的3D世界中摄象机照射的区域进行作画。他也能用于冲突检测。下面讲一下为什么要进行空间分割。假设你建立了一个游戏世界,这个世界有超过100,000个多边形要画。如果你建立一个循环并传递这些多边形,那速度是很慢的。即使你有一块很好的显示卡,他也会有很大的麻烦。但是玩你游戏的玩家的显示卡不会超过300$。有没有一种方法只渲染摄象机看见的多边形?那就是美丽的OCTREE。他允许你快速的找到你要渲染的多边形。 OCTREE是怎样工作的 OCTREE工作在立方体中。最初,OCTREE从根接点开始,这个根接点对齐于立方体中整个世界,水平或场景的axis中心线。因此,把我们的整个世界想象成一个不可见的立方体。
|
Woo算法
候选平面的方向朝前,用粗线
条表示,与射线之间的交点用
灰色表示。由于左边的相交点
距离射线原点最远,因此将该
点作为潜在相交点。
针对射线与AABB之间的相交检测,Woo提出了一些巧妙的优化
方法。
基本思想:在组成AABB的6个平面中选出3个候选平面。对于每
一对互相平行的平面来说,忽略其背向平面而不作进一步考虑。
计算射线与候选平面的相交距离(t值),其中的最大值就可能对应
一个相交情形。如果找到潜在的相交情形(相交点位于AABB的相
应面上) ,再计算出实际的相交点。
Intesection intersect( const Ray &one, const AxisAlignedBox &two )//Ray用参数表示则在0,1之间
{
OctreeSceneManager::intersect_call++;
// Null box?
if (two.isNull()) return OUTSIDE;
// Infinite box?
if (two.isInfinite()) return INTERSECT;
bool inside = true;
const Vector3& twoMin = two.getMinimum();
const Vector3& twoMax = two.getMaximum();
Vector3 origin = one.getOrigin();
Vector3 dir = one.getDirection();
Vector3 maxT(-1, -1, -1);
int i = 0;
for(i=0; i<3; i++ )
{
if( origin[i] < twoMin[i] )
{
inside = false;
if( dir[i] > 0 )
{
maxT[i] = (twoMin[i] - origin[i])/ dir[i];//循环一次,求出与三个平面相交的参数(0, 1)
}
}
else if( origin[i] > twoMax[i] )
{
inside = false;
if( dir[i] < 0 )
{
maxT[i] = (twoMax[i] - origin[i]) / dir[i];
}
}
}//--------------------------以上说明原点在包围盒内部,origin大于最小的点,小于最大的点
//参数为0--1
return INTERSECT;
if( inside )
{
return INTERSECT;
}
int whichPlane = 0;
if( maxT[1] > maxT[whichPlane])
whichPlane = 1;
if( maxT[2] > maxT[whichPlane])
whichPlane = 2; //求出最大的那个参数,就是潜在的求交平面
if( ((int)maxT[whichPlane]) & 0x80000000 )
{
return OUTSIDE;
}
for(i=0; i<3; i++ )
{
if( i!= whichPlane )
{
float f = origin[i] + maxT[whichPlane] * dir[i];
if ( f < (twoMin[i] - 0.00001f) || //如果小于最小值或大于最大值,则不向交
f > (twoMax[i] +0.00001f ) )
{
return OUTSIDE;
}
}
}
return INTERSECT;
}
Intersection intersect( const AxisAlignedBox &one, const AxisAlignedBox &two )
{
OctreeSceneManager::intersect_call++;
// Null box?
if (one.isNull() || two.isNull()) return OUTSIDE;
if (one.isInfinite()) return INSIDE;
if (two.isInfinite()) return INTERSECT;
const Vector3& insideMin = two.getMinimum();
const Vector3& insideMax = two.getMaximum();
const Vector3& outsideMin = one.getMinimum();
const Vector3& outsideMax = one.getMaximum();
if ( insideMax.x < outsideMin.x ||
insideMax.y < outsideMin.y ||
insideMax.z < outsideMin.z ||
insideMin.x > outsideMax.x ||
insideMin.y > outsideMax.y ||
insideMin.z > outsideMax.z )//最大值小于最小值,一定在外面
{
return OUTSIDE;
}
bool full = ( insideMin.x > outsideMin.x &&//内部最小的大于外部最小的,内部最大的小于外部最大的
insideMin.y > outsideMin.y &&
insideMin.z > outsideMin.z &&
insideMax.x < outsideMax.x &&
insideMax.y < outsideMax.y &&
insideMax.z < outsideMax.z );
if ( full )
return INSIDE;
else
return INTERSECT;
}
Intersection intersect( const Sphere &one, const AxisAlignedBox &two )
{
OctreeSceneManager::intersect_call++;
// Null box?
if (two.isNull()) return OUTSIDE;
if (two.isInfinite()) return INTERSECT;
float sradius = one.getRadius();
sradius *= sradius;
Vector3 scenter = one.getCenter();
const Vector3& twoMin = two.getMinimum();
const Vector3& twoMax = two.getMaximum();
float s, d = 0;
Vector3 mndistance = ( twoMin - scenter );
Vector3 mxdistance = ( twoMax - scenter );
if ( mndistance.squaredLength() < sradius &&//最大点及最小点到球心的距离均小于半径,则在包围盒内部
mxdistance.squaredLength() < sradius )
{
return INSIDE;
}
//find the square of the distance
//from the sphere to the box
for ( int i = 0 ; i < 3 ; i++ ) //在最小点的左边,并且到最小点的距离小于半径
{
if ( scenter[ i ] < twoMin[ i ] )
{
s = scenter[ i ] - twoMin[ i ]; //在最大点的右边,并且到最大点的距离大于半径
d += s * s;
}
else if ( scenter[ i ] > twoMax[ i ] )
{
s = scenter[ i ] - twoMax[ i ];
d += s * s;
}
}
bool partial = ( d <= sradius );
if ( !partial )
{
return OUTSIDE;
}
else
{
return INTERSECT;
}
}






