前言:softmax中的求导包含矩阵与向量的求导关系,记录的目的是为了回顾。
下图为利用softmax对样本进行k分类的问题,其损失函数的表达式为结构风险,第二项是模型结构的正则化项。
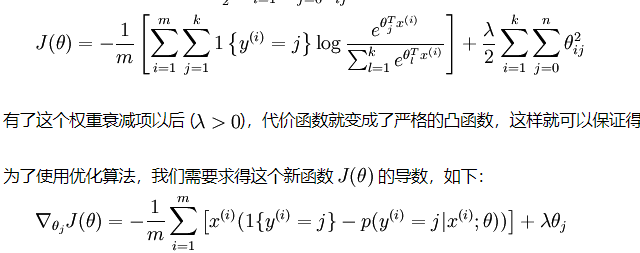
首先,每个queue:x(i)的特征维度是 n , 参数 θ 是一个 n×k 的矩阵,输出的结果 y(i) 为一个 k×1 的向量,其中第 j 个元素对应元素的 e 指数为该 queue 属于第 j 类的概率(未归一化)。所以虽然损失函数 J(θ) 是一个常数,但是它的自变量为一个矩阵 Θ 和 一个特征向量 x(i) ,这就牵涉到本文的重难点:矩阵、向量以及变量之间的求导。
更新 θj 的过程就是标量 J(θ) 对向量 θj 求导的过程,向量对标量求导的具体方式不想写,结论见文末,参考(https://blog.csdn.net/daaikuaichuan/article/details/80620518)。
第一项的求导过程:
将与 j 无关的乘项(-1/m)×∑i ×1{ j } 拉到最前面,对log中内容做变换得到((θj×x(i))) - log(∑L)。前者根据变量对向量求导可以得到为x(i),后者根据链式法则可以求出为{ [exp(θj*x(i)] / ∑L}* x(i), 与前面的项相乘就可以得到下式中的第一项。
第二项为 Θ 中所有列向量二范数之和,可以写成 ∑θjTθj ,其中与 θj 有关的内容为 θjTθj ,求导后为 2θj 。求导的结果为第二项。
J(θ) 对 θj 求导的结果如文中第二式。
标量对向量求导

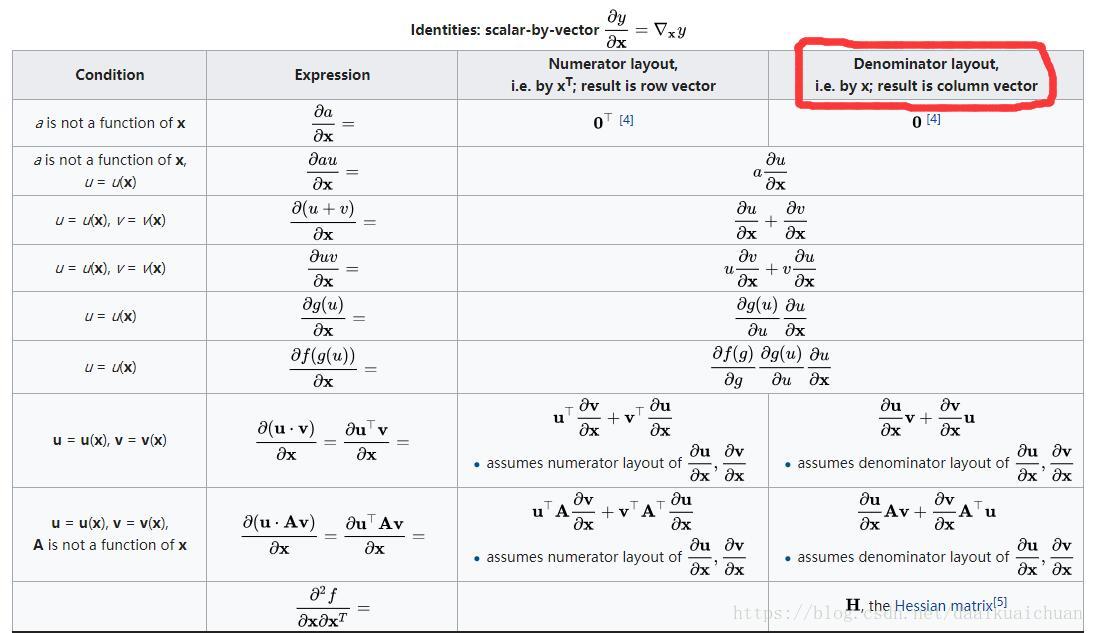
向量对标量求导

向量对向量求导
