浅谈树链剖分

树链剖分主要思想

RT，就是把一颗有根树按照dfs序放在一个连续线性数组当中，用数据结构维护区间操作

通常采用树状数组、线段树（平衡树qwq我不会）等维护

剖分的原则：链尽可能长(目的：减少上调操作)

size[x]表示以x为根节点的子树，有节点个数

重儿子：son[x]在x的诸多儿子中size[x]最大儿子的编号

于是就有重链：一条链沿着他的重儿子son[]走产生的一条链

剖分，每次dfs递归找到重链，剩下的就是轻链，

对于产生的每一条链放在一个连续的数组中（重新编号）用数据结构维护区间操作

两个dfs（预处理easy）：

dfs1处理：

x的重儿子son[x]

以x为根的子树节点个数 size[x]

节点x的深度dep[x]

节点x的父亲节点（root的father人为定义是0）

 程序：

int f[MAXN],dep[MAXN],son[MAXN],size[MAXN];
void dfs1(int u,int fa,int depth)//f[],dep[],son[],size[]
{
    f[u]=fa;dep[u]=depth;size[u]=1;
    for (int i=head[u];i;i=a[i].pre)
    {
        int v=a[i].to; if (v==fa) continue;
        dfs1(v,u,depth+1);
        size[u]+=size[v];
        if (size[son[u]]<size[v]) son[u]=v;
    }
}

dfs2处理

w[x]老编号为x在线性数据结构中的新编号（为了一条链连续）

top[x]节点x所在重链的链头所在元素的老编号 

*old[x]新编号为x节点的老编号

程序：

void dfs2(int u,int tp) //w[],top[],old[]
{
    w[u]=++cntw;top[u]=tp;
    old[cntw]=u;
    if (son[u]!=0) dfs2(son[u],tp);
    for (int i=head[u];i;i=a[i].pre)
    {
        int v=a[i].to; if (v==f[u]||v==son[u]) continue;
        dfs2(v,v);
    }
}

更新操作（mid）

将链u--v上所有元素都加上d

其实还好理解，参考代码（树状数组维护可以采用其他数据结构维护）

void change(int u,int v,int d) //此处u,v都为老编号
{
    int f1=top[u],f2=top[v];
    while (f1!=f2){
        if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v);
       //不同： 保证u这条链头比较深，处理u所在这条链上所有元素
        c1.update(w[f1],d);
        c1.update(w[u]+1,-d);
        c2.update(w[f1],d*(w[f1]-1));
        c2.update(w[u]+1,-d*w[u]);
        //树状数组维护一下
        u=f[f1];
        f1=top[u]; //上调到上面那条链
    }
    if (dep[u]<dep[v]) swap(u,v);
    c1.update(w[v],d);
    c1.update(w[u]+1,-d);
    c2.update(w[v],d*(w[v]-1));
    c2.update(w[u]+1,-d*w[u]);
    //树状数组维护一下 剩下的节点
}

查询操作（mid）

基于更新操作，也是调链的方式qwq，只是把维护改为求和

ll lca(int u,int v)//传入的为老编号
{
    int f1=top[u],f2=top[v];
    ll ret=0ll;
    while (f1!=f2){
        if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v);
        //w[f1]~w[u]
        ret=ret+getsum(w[f1],w[u]);
        u=f[f1];
        f1=top[u];
    }
    if (dep[u]<dep[v]) swap(u,v);
    //w[v]~w[u]
    ret=ret+getsum(w[v],w[u]);
    return ret%p;
}

错误（mistakes）

1.新编号老编号弄不清楚

2.链头迭代没写

3.维护的数据结构打错

模板（difficult）

注意：w[x]其实就是dfs序，一些奇怪的性质，子树上的dfs序都是连续的

维护一颗子树？直接维护编号w[x]到w[x]+size[x]-1这段区间里就行

P3384 【模板】树链剖分

题目描述

如题，已知一棵包含N个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

操作1： 格式： 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z

操作2： 格式： 2 x y 表示求树从x到y结点最短路径上所有节点的值之和

操作3： 格式： 3 x z 表示将以x为根节点的子树内所有节点值都加上z

操作4： 格式： 4 x 表示求以x为根节点的子树内所有节点值之和

输入输出格式

输入格式：

第一行包含4个正整数N、M、R、P，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含N个非负整数，分别依次表示各个节点上初始的数值。

接下来N-1行每行包含两个整数x、y，表示点x和点y之间连有一条边（保证无环且连通）

接下来M行每行包含若干个正整数，每行表示一个操作，格式如下：

操作1： 1 x y z

操作2： 2 x y

操作3： 3 x z

操作4： 4 x

输出格式：

输出包含若干行，分别依次表示每个操作2或操作4所得的结果（对P取模）

输入输出样例

输入样例#1： 

5 5 2 24
7 3 7 8 0 
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

输出样例#1： 

2
21

说明

时空限制：1s，128M

数据规模：

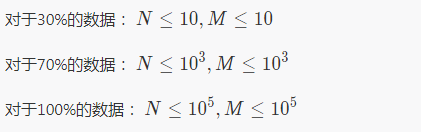
其实随机数据暴力维护是能过的，但是你觉得这可能是随机数据吗？

样例说明：

树的结构如下：

各个操作如下：

故输出应依次为2、21(重要的事情说三遍：记得取模)

代码：

# include <bits/stdc++.h>
# define Rint register int
# define MAXN 100005
using namespace std;
typedef long long ll;
int n,m,r,p,val[MAXN],b[MAXN];
struct Tree{
    ll c[MAXN];
    int lowbit(int x) { return x&(-x); }
    void update(int x,int y) {
        while (x<=n) {
            c[x]+=y; x+=lowbit(x);
        }
    }
    ll query(int x) {
        ll ret=0;
        while (x>0) {
            ret+=(ll)c[x]; x-=lowbit(x);
        }
        return ret;
    }
}c1,c2;
struct Edge{
    int pre,to;
}a[2*MAXN];
int tot=0,head[MAXN];
inline void adde(int u,int v)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    head[u]=tot;
}
inline int read()
{
    int X=0,w=0; char c=0;
    while(c<'0'||c>'9') {w|=c=='-';c=getchar();}
    while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar();
    return w?-X:X;
}
int f[MAXN],size[MAXN],dep[MAXN],son[MAXN];
inline void dfs1(int u,int fa,int depth)//f[],dep[],size[],son[]
{
    f[u]=fa; dep[u]=depth;size[u]=1;
    for (Rint i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fa) continue;
        dfs1(v,u,depth+1);
        size[u]+=size[v];
        if (size[son[u]]<size[v]) son[u]=v;
    }
}
int w[MAXN],cntw=0,top[MAXN],end[MAXN];
inline void dfs2(int u,int tp)//w[],top[]
{
    w[u]=++cntw;top[u]=tp;
    end[cntw]=u;
    if (son[u]!=0) dfs2(son[u],tp);
    for (Rint i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==f[u]) continue;
        if (v!=son[u]) dfs2(v,v);
    }
}
inline void change(int u,int v,int d)
{
    int f1=top[u],f2=top[v];
    while (f1!=f2){
        if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v);
        c1.update(w[f1],d);
        c1.update(w[u]+1,-d);
        c2.update(w[f1],d*(w[f1]-1));
        c2.update(w[u]+1,-d*(w[u]));
        u=f[f1];
        f1=top[u];
    }
    if (dep[u]>dep[v]) swap(u,v);
    c1.update(w[u],d);
    c1.update(w[v]+1,-d);
    c2.update(w[u],d*(w[u]-1));
    c2.update(w[v]+1,-d*(w[v]));
}
inline ll lca(int u,int v) //u,v都是老编号
{
    int f1=top[u],f2=top[v];
    ll ret=0;
    int l,r;
    while (f1!=f2){
        if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v);
        //求w[f1]~w[u]的区间和
        l=w[f1],r=w[u];
        ret=ret+r*c1.query(r)-c2.query(r)-((l-1)*c1.query(l-1)-c2.query(l-1));
        u=f[f1];
        f1=top[u];
    }
    if (dep[u]>dep[v]) swap(v,u);
    //求w[u]~w[v]区间和
    l=w[u],r=w[v];
    ret=ret+r*c1.query(r)-c2.query(r)-((l-1)*c1.query(l-1)-c2.query(l-1));
    return ret%p;
}
inline void print(ll x)
{
    if(x<0){ putchar('-');x=-x;}
    if(x>9) print(x/10);
    putchar(x%10+'0');
}
int main()
{
    n=read();m=read();r=read();p=read();
    for (int i=1;i<=n;i++) val[i]=read();
    int u,v;
    for (Rint i=1;i<=n-1;i++) {
        u=read();v=read();
        adde(u,v); adde(v,u);
    }
    dfs1(r,0,0);
    dfs2(r,0);
    for (Rint i=1;i<=n;i++) b[i]=val[end[i]];
    for (Rint i=1;i<=n;i++) c1.update(i,b[i]-b[i-1]),c2.update(i,(b[i]-b[i-1])*(i-1));
    int op,x,y,z;
    for (Rint i=1;i<=m;i++) {
        op=read();x=read();
        if (op==1) y=read(),z=read(),change(x,y,z);
        else if (op==2) y=read(),print(lca(x,y)),putchar('
');
        else if (op==3) {
        y=read();c1.update(w[x],y);c1.update(w[x]+size[x]-1+1,-y);
        c2.update(w[x],(w[x]-1)*y); c2.update(w[x]+size[x]-1+1,-y*(w[x]+size[x]-1+1-1));//w[x]~w[x]+size(x)-1+1 +y
        }
        else if (op==4) {
           int l=w[x],r=w[x]+size[x]-1;
           ll ans=r*c1.query(r)-c2.query(r)-((l-1)*c1.query(l-1)-c2.query(l-1));
           print(ans%p);
           putchar('
');
        }
    }
    return 0;
}

P2590 [ZJOI2008]树的统计

题目描述

一棵树上有n个节点，编号分别为1到n，每个节点都有一个权值w。

我们将以下面的形式来要求你对这棵树完成一些操作：

I. CHANGE u t : 把结点u的权值改为t

II. QMAX u v: 询问从点u到点v的路径上的节点的最大权值

III. QSUM u v: 询问从点u到点v的路径上的节点的权值和

注意：从点u到点v的路径上的节点包括u和v本身

输入输出格式

输入格式：

输入文件的第一行为一个整数n，表示节点的个数。

接下来n – 1行，每行2个整数a和b，表示节点a和节点b之间有一条边相连。

接下来一行n个整数，第i个整数wi表示节点i的权值。

接下来1行，为一个整数q，表示操作的总数。

接下来q行，每行一个操作，以“CHANGE u t”或者“QMAX u v”或者“QSUM u v”的形式给出。

输出格式：

对于每个“QMAX”或者“QSUM”的操作，每行输出一个整数表示要求输出的结果。

输入输出样例

输入样例#1： 

4
1 2
2 3
4 1
4 2 1 3
12
QMAX 3 4
QMAX 3 3
QMAX 3 2
QMAX 2 3
QSUM 3 4
QSUM 2 1
CHANGE 1 5
QMAX 3 4
CHANGE 3 6
QMAX 3 4
QMAX 2 4
QSUM 3 4

输出样例#1： 

4
1
2
2
10
6
5
6
5
16

说明

对于100％的数据，保证1<=n<=30000，0<=q<=200000；中途操作中保证每个节点的权值w在-30000到30000之间。

# include <cstring>
# include <iostream>
# include <cstdio>
# include <climits>
# define Rint register int
using namespace std;
typedef long long ll;
const int MAXN=60010;
int b[MAXN],n,val[MAXN];
inline int read()
{
    int X=0,w=0; char c=0;
    while(c<'0'||c>'9') {w|=c=='-';c=getchar();}
    while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar();
    return w?-X:X;
}
struct TreeMax{
    int f[3*MAXN],s[3*MAXN],opx,opl,opr,ans;
    inline void build(int x,int l,int r)
    {
        if (l==r) { f[x]=b[l]; return;}
        int m=(l+r)>>1;
        build(x<<1,l,m);
        build((x<<1)+1,m+1,r);
        f[x]=max(f[x<<1],f[(x<<1)+1]);
    }
    inline void _update(int x,int l,int r)
    {

        if (opl<=l&&opr>=r) f[x]=opx;
        if (l==r) return;
        int m=(l+r)>>1;
        if (opl<=m) _update(x<<1,l,m);
        if (opr>m)  _update((x<<1)+1,m+1,r);
        f[x]=max(f[x<<1],f[(x<<1)+1]);
    }
    inline void _query(int x,int l,int r)
    {
        if (opl<=l&&opr>=r) {
            ans=max(ans,f[x]);
            return;
        }
        if (l==r) return;
        int m=(l+r)>>1;
        if (opl<=m) _query(x<<1,l,m);
        if (opr>m)  _query((x<<1)+1,m+1,r);
    }
    inline int query(int l,int r) {
        ans=-INT_MAX;
        opl=l;opr=r;
        _query(1,1,n);
        return ans;
    }
    inline void update(int l,int r,int w)
    {
        opx=w;opl=l;opr=r;
        _update(1,1,n);
    }
}fmax;
struct TreeSum{
    int opx,opl,opr;
    ll f[3*MAXN],ans;
    inline void build(int x,int l,int r)
    {
        if (l==r) { f[x]=(ll)b[l]; return;}
        int m=(l+r)>>1;
        build(x<<1,l,m);
        build((x<<1)+1,m+1,r);
        f[x]=f[x<<1]+f[(x<<1)+1];
    }
    inline void _update(int x,int l,int r)
    {
        if (opl<=l&&opr>=r) f[x]=(ll) (r-l+1)*opx;
        if (l==r) return;
        int m=(l+r)>>1;
        if (opl<=m) _update(x<<1,l,m);
        if (opr>m)  _update((x<<1)+1,m+1,r);
        f[x]=f[x<<1]+f[(x<<1)+1];
    }
    inline void _query(int x,int l,int r)
    {
        if (opl<=l&&opr>=r) {
            ans=ans+(ll)f[x];
            return;
        }
        int m=(l+r)>>1;
        if (opl<=m) _query(x<<1,l,m);
        if (opr>m)  _query((x<<1)+1,m+1,r);
    }
    inline  ll query(int l,int r) {
        ans=0ll;
        opl=l;opr=r;
        _query(1,1,n);
        return ans;
    }
    inline void update(int l,int r,int w)
    {
        opx=w;opl=l;opr=r;
        _update(1,1,n);
    }
}fsum;
struct rec{
    int pre,to;
}a[MAXN*2];
int tot=0,head[MAXN];
inline void adde(int u,int v)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    head[u]=tot;
}
int f[MAXN],size[MAXN],dep[MAXN],son[MAXN];
inline void dfs1(int u,int fa,int depth)
{
    f[u]=fa;size[u]=1;dep[u]=depth;
    for (Rint i=head[u];i;i=a[i].pre)
    {
        int v=a[i].to;
        if (v==fa) continue;
        dfs1(v,u,depth+1);
        size[u]+=size[v];
        if (size[son[u]]<size[v]) son[u]=v;
    }
}
int w[MAXN],top[MAXN],old[MAXN],cntw=0;
inline void dfs2(int u,int tp)
{
    w[u]=++cntw;top[u]=tp;
    old[cntw]=u;
    if (son[u]!=0) dfs2(son[u],tp);
    for (Rint i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==f[u]||v==son[u]) continue;
        dfs2(v,v);
    }
}
inline int lcamax(int u,int v)
{
    int f1=top[u],f2=top[v],ret=-INT_MAX;
    while (f1!=f2){
        if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v);
        int l=w[f1],r=w[u];
        ret=max(ret,fmax.query(l,r));
        u=f[f1];
        f1=top[u];
    }
    if (dep[u]<dep[v]) swap(u,v);
    int l=w[v],r=w[u];
    ret=max(ret,fmax.query(l,r));
    return ret;
}
inline ll lcasum(int u,int v)
{
    int f1=top[u],f2=top[v];
    ll ret=0;
    while (f1!=f2){
        if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v);
        int l=w[f1],r=w[u];
        ret=ret+fsum.query(l,r);
        u=f[f1];
        f1=top[u];
    }
    if (dep[u]<dep[v]) swap(u,v);
    int l=w[v],r=w[u];
    ret=ret+fsum.query(l,r);
    return ret;
}
inline void writeint(int x)
{
    if (x<0) { putchar('-'); x=-x;}
    if (x>9) writeint(x/10);
    putchar(x%10+'0');
}
inline void writell (ll x)
{
    if (x<0ll) {putchar('-');x=-x;}
    if (x>9ll) writell(x/10);
    putchar(x%10ll+'0');
}
inline void change(int x,int y)
{
    int l=w[x];
    fmax.update(l,l,y);
    fsum.update(l,l,y);
}
char s[50];
int main()
{
    n=read();
    int u,v;
    for (Rint i=1;i<=n-1;i++) {
        u=read();v=read();
        adde(u,v); adde(v,u);
    }
    dfs1(1,0,0);
    dfs2(1,0);
    for (Rint i=1;i<=n;i++) val[i]=read();
    for (Rint i=1;i<=n;i++) b[i]=val[old[i]];
    fmax.build(1,1,n);
    fsum.build(1,1,n);
    int m; m=read();
    int x,y;
    for (Rint i=1;i<=m;i++){
        scanf("%s",s); x=read(); y=read();
        if (s[1]=='M') writeint(lcamax(x,y)),putchar('
');
        else if (s[1]=='S') writell(lcasum(x,y)),putchar('
');
        else if (s[1]=='H') change(x,y);
    }
    return 0;
}