R数据挖掘 第三篇：聚类的评估（簇数确定和轮廓系数）和可视化

在实际的聚类应用中，通常使用k-均值和k-中心化算法来进行聚类分析，这两种算法都需要输入簇数，为了保证聚类的质量，应该首先确定最佳的簇数，并使用轮廓系数来评估聚类的结果。

一，k-均值法确定最佳的簇数

通常情况下，使用肘方法（elbow）以确定聚类的最佳的簇数，肘方法之所以是有效的，是基于以下观察：增加簇数有助于降低每个簇的簇内方差之和，给定k>0，计算簇内方差和var(k)，绘制var关于k的曲线，曲线的第一个（或最显著的）拐点暗示正确的簇数。

1，使用sjc.elbow()函数计算肘值

sjPlot包中sjc.elbow()函数实现了肘方法，用于计算k-均值聚类分析的肘值，以确定最佳的簇数：

library(sjPlot)
sjc.elbow(data, steps = 15, show.diff = FALSE)

参数注释：

• steps：最大的肘值的数量
• show.diff：默认值是FALSE，额外绘制一个图，连接每个肘值，用于显示各个肘值之间的差异，改图有助于识别“肘部”，暗示“正确的”簇数。

sjc.elbow()函数用于绘制k-均值聚类分析的肘值，该函数在指定的数据框计算k-均值聚类分析，产生两个图形：一个图形具有不同的肘值，另一个图形是连接y轴上的每个“步”，即在相邻的肘值之间绘制连线，第二个图中曲线的拐点可能暗示“正确的”簇数。

绘制k均值聚类分析的肘部值。 该函数计算所提供的数据帧上的k均值聚类分析，并产生两个图：一个具有不同的肘值，另一个图绘制在y轴上的每个“步”（即在肘值之间）之间的差异。 第二个图的增加可能表明肘部标准。

library(effects)
library(sjPlot)
library(ggplot2)

sjc.elbow(data,show.diff = FALSE)

从下面的肘值图中，可以看出曲线的拐点大致在5附近：

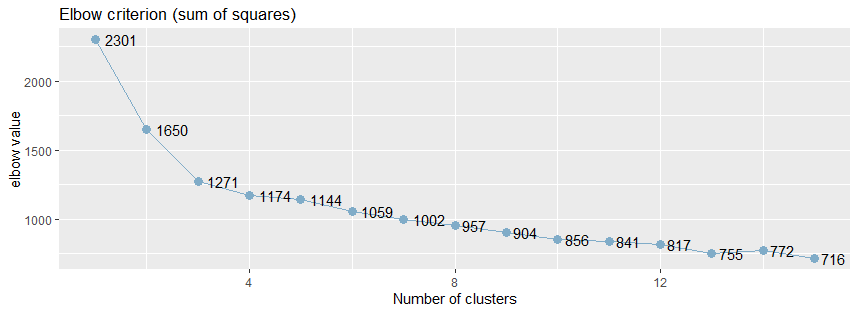
2，使用NbClust()函数来验证肘值

从上面肘值图中，可以看到曲线的拐点是3，还可以使用NbClust包种的NbClust()函数，默认情况下，该函数提供了26个不同的指标来帮助确定簇的最终数目。

NbClust(data = NULL, diss = NULL, distance = "euclidean", min.nc = 2, max.nc = 15, method = NULL, index = "all", alphaBeale = 0.1)

参数注释：

• diss：相异性矩阵（dissimilarity matrix），默认值是NULL，如果diss参数不为NULL，那么忽略distance参数。
• distance：用于计算相异性矩阵的距离度量，有效值是： "euclidean", "maximum", "manhattan", "canberra", "binary", "minkowski" 和"NULL"。如果distance不是NULL，diss（相异性矩阵）参数必须为NULL。
• min.nc：最小的簇数
• max.nc：最大的簇数
• method：用于聚类分析的方法，有效值是："ward.D", "ward.D2", "single", "complete", "average", "mcquitty", "median", "centroid", "kmeans"
• index：用于计算的指标，NbClust()函数提供了30个指数，默认值是"all"，是指除GAP、Gamma、Gplus 和 Tau之外的26个指标。
• alphaBeale：Beale指数的显著性值

利用NbClust()函数来确定k-均值聚类的最佳簇数：

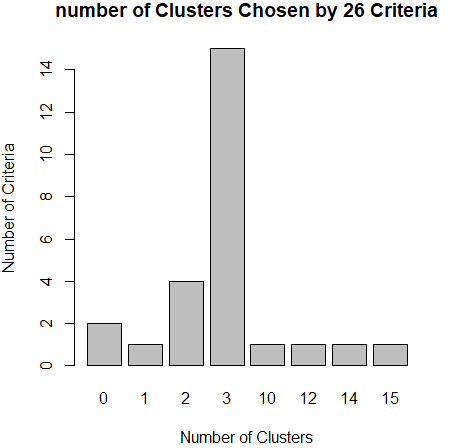
library(NbClust)

nc <- NbClust(data,min.nc = 2,max.nc = 15,method = "kmeans")
barplot(table(nc$Best.nc[1,]),xlab="Number of Clusters",ylab="Number of Criteria",main="number of Clusters Chosen by 26 Criteria")

从条形图种，可以看到支持簇数为3的指标（Criteria）的数量是最多的，因此，基本上可以确定，k-均值聚类的簇数目是3。

二，k-中心化确定最佳簇数

k-中心化聚类有两种实现方法，PAM和CLARA，PAM适合在小型数据集上运行，CLARA算法基于抽样，不考虑整个数据集，而是使用数据集的一个随机样本，然后使用PAM方法计算样本的最佳中心点。

通过fpc包中的pamk()函数得到最佳簇数：

pamk(data,krange=2:10,criterion="asw", usepam=TRUE,
     scaling=FALSE, alpha=0.001, diss=inherits(data, "dist"),
     critout=FALSE, ns=10, seed=NULL, ...)

参数注释：

• krange：整数向量，用于表示簇的数量
• criterion：有效值是："asw"（默认值）、 "multiasw" 和 "ch"
• usepam：逻辑值，如果设置为TRUE，那么使用pam算法，如果为FALSE，那么使用clara算法。
• scaling：逻辑值，是否对数据进行缩放（标准化），如果设置为FALSE，那么不对data参数做任何缩放；如果设置为TRUE，那么对data参数通过把（中间）变量除以它们的均方根来完成缩放。
• diss：逻辑值，如果设置为TRUE，表示data参数是相异性矩阵；如果设置为FALSE，那么data参数是观测矩阵。

使用pamk()函数获得PAM或CLARA聚类的最佳簇数：

library(fpc)
pamk.best <- pamk(dataset)
pamk.best$nc

通过cluster包中的clusplot()函数来查看聚类的结果：

library(cluster)
clusplot(pam(dataset, pamk.best$nc))

三，评估聚类的质量（轮廓系数）

使用数据集中对象之间的相似性度量来评估聚类的质量，轮廓系数（silhouette coefficient）就是这种相似性度量，是簇的密集与分散程度的评价指标。轮廓系数的值在-1和1之间，该值越接近于1，簇越紧凑，聚类越好。当轮廓系数接近1时，簇内紧凑，并远离其他簇。

如果轮廓系数sil 接近1，则说明样本聚类合理；如果轮廓系数sil 接近-1，则说明样本i更应该分类到另外的簇；如果轮廓系数sil 近似为0，则说明样本i在两个簇的边界上。所有样本的轮廓系数 sil的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。

1，fpc包

包fpc中实现了计算聚类后的一些评价指标，其中就包括了轮廓系数：avg.silwidth（平均的轮廓宽度）

library(fpc)
result <- kmeans(data,k)
stats <- cluster.stats(dist(data)^2, result$cluster)
sli <- stats$avg.silwidth

2，silhouette()函数

包cluster中计算轮廓系数的函数silhouette()，返回聚类的平均轮廓宽度：

silhouette(x, dist, dmatrix, ...)

参数注释：

• x：整数向量，是聚类算法的结果
• dist：相异性矩阵（是dist()函数计算的结果），如果dist参数不指定，那么dmatrix参数必须指定；
• dmatrix：对称性的相异性矩阵，用于代替dist参数，比dist参数更有效率

使用silhouette()计算轮廓系数：

library (cluster)
library (vegan)

#pam
dis <- vegdist(data)
res <- pam(dis,3) 
sil <- silhouette (res$clustering,dis)

#kmeans
dis <- dist(data)^2
res <- kmeans(data,3)
sil <- silhouette (res$cluster, dis)

四，聚类的可视化

聚类的结果，可以试用ggplot2来可视化，还可以使用的一些聚类包中特有的函数来实现：factoextra包，sjPlot包和cluster包

1，cluster包

clusplot()函数

2，sjPlot包

sjc.qclus()函数

3，factoextra包

该包中的两个函数十分有用，一个用于确定最佳的簇数，一个用于可视化聚类的结果。

（1），确定最佳的簇数fviz_nbclust()

函数fviz_nbclust()，用于划分聚类分析中，使用轮廓系数，WSS（簇内平方误差和）确定和可视化最佳的簇数

fviz_nbclust(x, FUNcluster = NULL, method = c("silhouette", "wss",), diss = NULL, k.max = 10, ...)

参数注释：

• FUNcluster：用于聚类的函数，可用的值是： kmeans, cluster::pam, cluster::clara, cluster::fanny, hcut等
• method：用于评估最佳簇数的指标
• diss：相异性矩阵，由dist()函数产生的对象，如果设置为NULL，那么表示使用 dist(data, method="euclidean") 计算data参数，得到相异性矩阵；
• k.max：最大的簇数量，至少是2

 例如，使用kmenas进行聚类分析，使用平均轮廓宽度来评估聚类的簇数：

library(factoextra)
fviz_nbclust(dataset, kmeans, method = "silhouette")

（2），可视化聚类的结果

fviz_cluster()函数用于可是化聚类的结果：

fviz_cluster(object, data = NULL, choose.vars = NULL, stand = TRUE,
  axes = c(1, 2), geom = c("point", "text"), repel = FALSE,
  show.clust.cent = TRUE, ellipse = TRUE, ellipse.type = "convex",
  ellipse.level = 0.95, ellipse.alpha = 0.2, shape = NULL,
  pointsize = 1.5, labelsize = 12, main = "Cluster plot", xlab = NULL,
  ylab = NULL, outlier.color = "black", outlier.shape = 19,
  ggtheme = theme_grey(), ...)

参数注释：

• object：是聚类函数计算的结果
• data：原始对象数据集

使用fviz_cluster()把聚类的结果显示出来：

km.res <- kmeans(dataset,3)
fviz_cluster(km.res, data = dataset)

参考文档：

确定最佳聚类数目的10种方法