浅谈ST表

ST表用来解决RMQ问题，即Range Maxinum（Mininum）Query，寻找某个静态序列的区间最大/最小值

一、预处理

ST表的原理是dp，设f[i][j]表示从a[i]到a[i+2^j-1]的最小值，那么我们可以对原序列进行一些划分

像这样，左右两个区间再次这么划分

以求最大值为例，总区间的最大值=max（左区间最大值，右区间最大值）

即状态转移方程为f[x][j]=max(f[x][j-1],f[x+2^j-1][j-1]

预处理的时间复杂度为O（nlogn）

 

二、对于询问求解

询问区间[l,r]的最大值

我们设x=log₂l-r+1

那么答案就是max（f[l][x],f[r-2^x+1][x]）

如图：

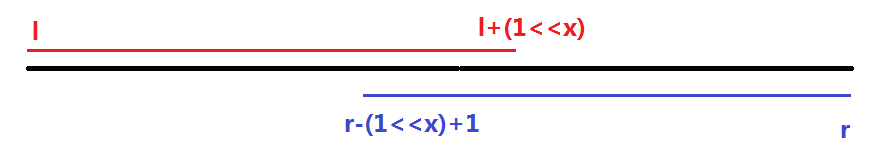
黑色的最大值为红色最大值与蓝色最大值的较大值

查找的时间复杂度为O（1）

三、模板

给你n个数，每次询问区间[l,r]的最大值（n≤100000，询问次数≤1000000）

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
#define MAXN 100005
using namespace std;

inline int read()
{
    int f=1,x=0;
    char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-') f=-1; ch=getchar();}
    while(ch>='0' && ch<='9') {x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}

int n,m;
int Log[MAXN],f[MAXN][20];

int main()
{
    int i,j,a,b,s;
    n=read();
    m=read();
    Log[0]=-1;
    for(i=1;i<=n;i++)
    {
        f[i][0]=read();
        Log[i]=Log[i>>1]+1;
    }
    for(j=1;j<=18;j++)
        for(i=1;i+(1<<j)-1<=n;i++)
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    for(i=1;i<=m;i++)
    {
        a=read(); b=read();
        s=Log[b-a+1];
        printf("%d
",max(f[a][s],f[b-(1<<s)+1][s]));
    }
    return 0;
}

四、ST表与线段树的比较

ST表对于静态区间可以做到O(nlogn)预处理，O(1)查询最大值，而且代码实现简单

线段树则支持修改与其他操作

本文部分内容参考《信息学奥赛一本通.提高篇》第四章第二章 RMQ问题

如需转载，请注明https://www.cnblogs.com/llllllpppppp/p/10049374.html