Trie树,也叫字典树。顾名思义,它就是一个字典
字典是干什么的?查找单词!(英文字典哦)
个人认为字典树这个名字起得特别好,因为它真的跟字典特别像,一会r你就知道了。
注:trie的中文翻译就是单词查找树
一、引入
先来看一个题:
给你n个单词构成一个字典,再给你一个单词,问此单词在字典中有没有出现。
简单,暴力!
时间复杂度:n*单词长度
再来看一个题:
给你n个单词构成一个字典,再给你m个单词,问这m个单词在字典中有没有出现。
再暴力!
时间复杂度:n*单词长度+m*n*单词长度
n≤1e4,m≤1e4,单词长度≤1e3
boom!
(╯‵□′)╯︵┻━┻
所以,为什么要学习使用Trie树?
因为它快!
二、概念
我们首先来看看Trie树是啥
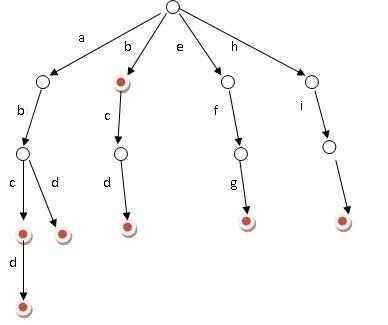
↑就是它
我们来解剖一下,好好研究研究(Trie树:瑟瑟发抖)
首先,我们发现树的每条边上都有一个字母
这就是Trie树的样子,每条边上都有一个字母,每个顶点代表从根到该节点的路径所对应的字符串(根结点除外)
其次,有些节点是红色的,有些则不是
这是什么意思呢?
结点不是代表单词嘛
所以如果结点标红,代表该单词在字典中实际出现过
如果看不太懂,不要紧,继续往下
三、插入单词(构建Trie树)
这里进入正题。第一步,构建trie树
就好比你想要查找单词,首先得有字典才行吧
step1:初始化
Trie树为空,只包含一个孤零零的根结点

step2:插入单词(注:这里假设所有单词仅由小写字母构成)
插入一个单词的步骤如下:
(1)对于Trie树,我们从根结点开始,设该节点为P;对于这个单词,我们从第一个字母开始,设此字符为s
(2)扫描P下方的所有边,看s有没有出现过
如果出现了,设s与P→Q这条边上的字符相同,则P=Q
如果没有出现,另建一条边,使该边上的字母为s,新节点为Q,然后P=Q
(3)s变为该单词的下一个字符,重复步骤2,直到扫描完整个单词为止
以概念中的那个图为例
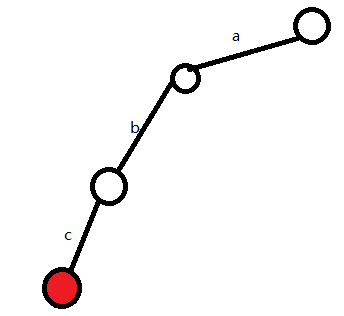
首先我们要插入abc这个单词
(1)P为根结点,s为'a'
发现根结点下方无'a',所以新建一条边
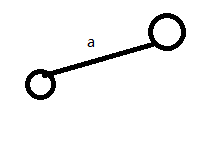
(2)P为a下方那个结点,s为'b'
发现P下方无'b',所以新建一条边
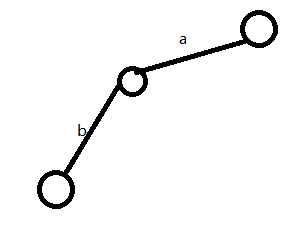
(3)P为b下方那个结点,s为'c'
发现P下方无'c',所以新建一条边
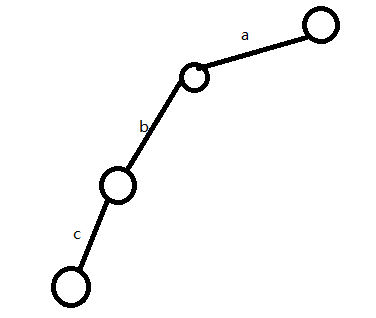
(4)发现abc这个单词插入完成,所以在当前的s做个标记,表示abc是一个出现过的单词
接着我们按照相同的步骤插入bcd、efg和hij
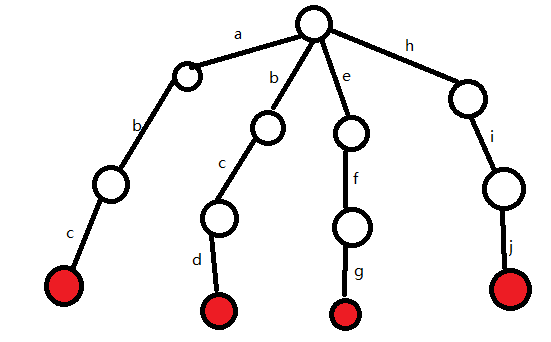
接下来插入abcd
(1)P为根结点,s为'a'
发现根结点下方有'a',所以P变为'a'下方的结点
(2)P为a下方那个结点,s为'b'
发现P下方有'b',所以P变为'b'下方的结点
(3)P为b下方那个结点,s为'c'
发现P下方有'c',所以P变为'c'下方的结点
(4)P为c下方那个红色的结点,s为'd'
发现P下方无'd',所以所以新建一条边
(5)单词abcd插入完毕,将当前的s做标记
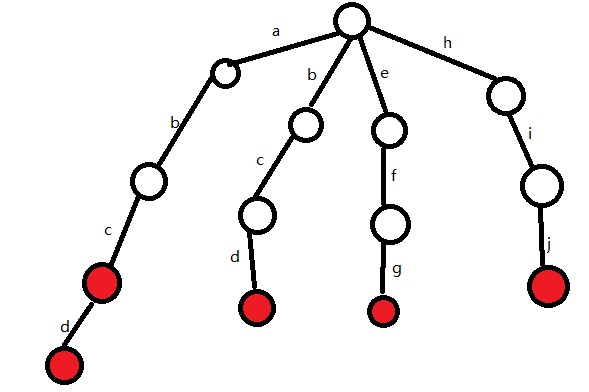
下面按照相同的方法,继续插入单词abd和b
插入完成后Trie树如下:
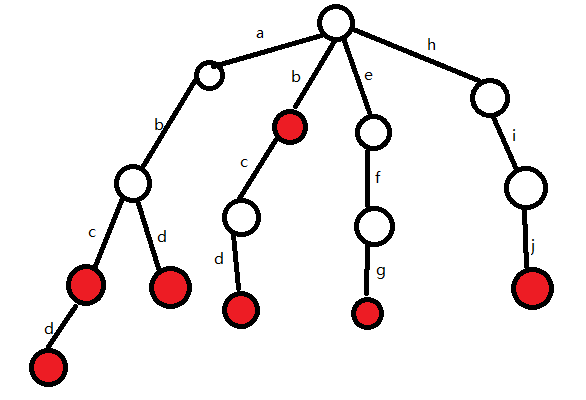
看看一样不:

(右下那条边应该是j)
我们可以发现,在Trie树中有相同前缀的单词共用相同的前缀,这样就可以大大的优化空间和时间
插入单词的时间复杂度为O(NE)(N为单词个数,E为单词长度)
参考代码:

void insert(char *s)//s为要插入的字符串 { int len=strlen(s); int u=1;//1为根节点 for(int i=0;i<len;i++) { int c=s[i]-'a';//'a'有时需换成'A'或'0' if(!trie[u][c])//没有共同前缀,建立一个新的 ch[u][c]=++tot;//tot为总点数 u=ch[u][c];//继续向下插入单词 } book[u]=true;//标记是一个出现过的单词(图中涂红色) }
四、查找单词
词典有了,接下来就可以查词了
在trie树中查单词就跟查字典一样。先查首字母,然后第二个,第三个……
查找过程跟插入的过程很像:
(1)对于Trie树,我们从根结点开始,设该节点为P;对于这个单词,我们从第一个字母开始,设此字符为s
(2)扫描P下方的所有边,看s有没有出现过
如果出现了,设s与P→Q这条边上的字符相同,则P=Q
如果没有出现,则该单词没有出现过,直接返回false
(3)s变为该单词的下一个字符,重复步骤2,直到扫描完整个单词为止
(4)扫描完成后,判断节点P有没有被标记(是不是某个出现过的单词的结尾)。如果标记了,那么该单词出现过,返回true;如果没有标记,那么该单词是词典中这个单词的前缀,返回false。
对于(4)讲解一下:
还是这棵Trie树:

我们查找ef这个单词:
(1)P为根结点,s为'e'
发现根结点下方有'e',所以P变为'e'下方的结点
(2)P为e下方那个结点,s为'f'
发现P下方有'f',所以P变为'f'下方的结点
(3)查找完成,发现P这里没有标记,所以ef是词典中单词efg的前缀,而不是直接出现在了词典里,返回false
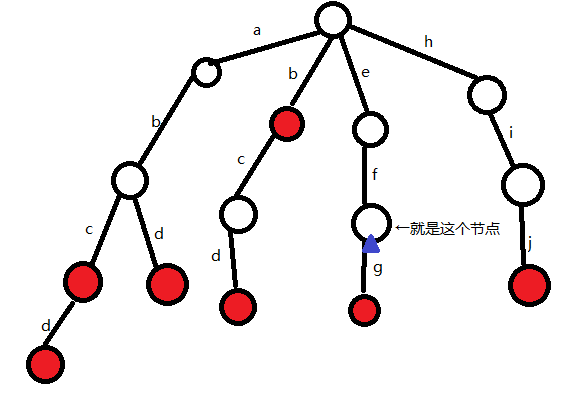
再举一个例子,我们查找abd这个单词:
(1)P为根结点,s为'a'
发现根结点下方有'a',所以P变为'a'下方的结点
(2)P为a下方那个结点,s为'b'
发现P下方有'b',所以P变为'b'下方的结点
(3)P为b下方那个结点,s为'd'
发现P下方有'd',所以P变为'd'下方的结点
(3)查找完成,发现P这里有标记,所以abd是词典中的单词,返回true
应该讲的挺明白的
查找的一个单词的时间复杂度O(E),比起暴力的O(NE)要快多了
参考代码:

bool find(char *s)//s为要查找的字符串 { int len=strlen(s); int u=1;//1为根节点 for(int i=0;i<len;i++) { int c=s[i]-'a';//'a'有时需换成'A'或'0' if(!trie[u][c])//单词没有出现,直接返回false return false; u=ch[u][c];//继续向下查找单词 } //如果扫描完了这个单词 return true;//是某个单词的前缀 }

bool find(char *s)//s为要查找的字符串 { int len=strlen(s); int u=1;//1为根节点 for(int i=0;i<len;i++) { int c=s[i]-'a';//'a'有时需换成'A'或'0' if(!trie[u][c])//单词没有出现,直接返回false return false; u=ch[u][c];//继续向下查找单词 } //如果扫描完了这个单词 return book[u];//如果出现过,返回true;如果没有出现过(是前缀),返回false }
模板题:
https://www.cnblogs.com/llllllpppppp/p/9366344.html
本文部分图片来源于网络
部分内容参考《信息学奥赛一本通.提高篇》第二部分第三章 Trie字典树
若需转载,请注明https://www.cnblogs.com/llllllpppppp/p/9449846.html
~祝大家编程顺利~
