[概率]Lucky Coins

题目描述

Bob has collected a lot of coins in different kinds. He wants to know which kind of coins is lucky. He finds out a lucky kind of coins by the following way. He tosses all the coins simultaneously, and then removes the coins that come up tails. He then tosses all the remaining coins and removes the coins that come up tails. He repeats the previous step until there is one kind of coins remaining or there are no coins remaining. If there is one kind of coins remaining, then this kind of coins is lucky. Given the number of coins and the probability that the coins come up heads after tossing for each kind, your task is to calculate the probability for each kind of coins that will be lucky.

输入

The first line is the number of test cases. For each test case, the first line contains an integer k representing the number of kinds. Each of the following k lines describes a kind of coins, which contains an integer and a real number representing the number of coins and the probability that the coins come up heads after tossing. It is guaranteed that the number of kinds is no more than 10, the total number of coins is no more than 1000000, and the probabilities that the coins come up heads after tossing are between 0.4 and 0.6.

输出

For each test case, output a line containing k real numbers with the precision of 6 digits, which are the probabilities of each kind of coins that will be lucky.

样例输入

复制样例数据

3
1
1000000 0.5
2
1 0.4
1 0.6
3
2 0.4
2 0.5
2 0.6

样例输出

1.000000
0.210526 0.473684
0.124867 0.234823 0.420066

思路：算出die[i][j]=(1-p[i]^j)^num[i]表示第i种硬币在第j轮之前死光的概率，以及alive[i][j]=1.0-die[i][j]表示第i种硬币在第j轮时还没死光的概率。
则假设在第j轮时第i种硬币成为了lucky coin，此概率将等于(∏u=1~k&&u!=idie[u][j]-∏u=1~k&&u!=idie[u][j-1])*alive[i][j]; 因为此概率等于（恰好在第j轮其他硬币全死光的概率）*（第j轮第i种硬币还活着的概率）。
则第i种硬币成为lucky coin的总概率为

。

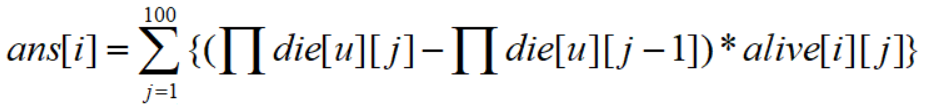AC代码：

#include<bits/stdc++.h>
using namespace std;

int num[15];
double p[15];
double die[15][105],alive[15][105];
double ans[15];

int main()
{
    int _;scanf("%d",&_);
    while(_--){
        int k;scanf("%d",&k);
        for(int i=1;i<=k;i++){
            scanf("%d%lf",&num[i],&p[i]);
        }

        if(k==1){
            printf("1.000000
");
            continue;
        }

        for(int i=1;i<=k;i++){
            for(int j=1;j<=100;j++){
                die[i][j]=pow((1.0-pow(p[i],j)),num[i]);
                alive[i][j]=1.0-die[i][j];
            }
        }


        for(int i=1;i<=k;i++){
            ans[i]=0.0;
            for(int j=1;j<100;j++){
                double tmp1=1.0,tmp2=1.0;
                for(int u=1;u<=k;u++){
                    if(u!=i) {
                        tmp1*=die[u][j-1];
                        tmp2*=die[u][j];
                    }
                }
                ans[i]+=(tmp2-tmp1)*alive[i][j];
            }
        }

        for(int i=1;i<=k;i++){
            if(i!=1) printf(" ");
            printf("%.6f",ans[i]);
        }
        printf("
");
    }
    return 0;
}