题目描述
Ian's going to California, and he has to pack his things, including his collection of cirles. Given a set of cirles, your program must find the smallest rectangular box in which they fit.
All cirles must touch the bottom of the box. The figure below shows an acceptable packing for a set of cirles (although this may not be the optimal packing for these partiular cirles). Note that in an ideal packing, each cirle should touch at least one other cirle (but you probably figured that out).

All cirles must touch the bottom of the box. The figure below shows an acceptable packing for a set of cirles (although this may not be the optimal packing for these partiular cirles). Note that in an ideal packing, each cirle should touch at least one other cirle (but you probably figured that out).

输入
The first line of input contains a single positive decimal integer n, n < 50. This indicates the number of lines which follow. The subsequent n lines each contain a series of numbers separated by spaces.
The first number on each of these lines is a positive integer m, m < 8, which indicates how many other numbers appear on that line. The next m numbers on the line are the radii of the cirles which must be packed in a single box. These numbers need not be integers.
The first number on each of these lines is a positive integer m, m < 8, which indicates how many other numbers appear on that line. The next m numbers on the line are the radii of the cirles which must be packed in a single box. These numbers need not be integers.
输出
For each data line of input, excluding the first line of input containing n, your program must output the size of the smallest rectangle which an pack the cirles. Each case should be output on a separate line by itself, with three places after the decimal point. Do not output leading zeroes unless the number is less than 1, e.g. 0.543.
样例输入
3
3 2.0 1.0 2.0
4 2.0 2.0 2.0 2.0
3 2.0 1.0 4.0
样例输出
9.657 16.000 12.657
思路:dfs n!种全排列,计算每种排列所需长度,取最小
计算长度:
1.计算两相切圆在x方向上的距离L:
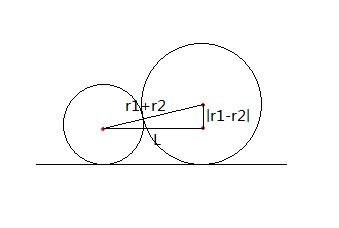
2.让第一个圆与直线x=0相切,根据以上方法确定当前排列的每一个圆的圆心x坐标
注意:
1)
第i个圆不一定是与第i-1个圆相切
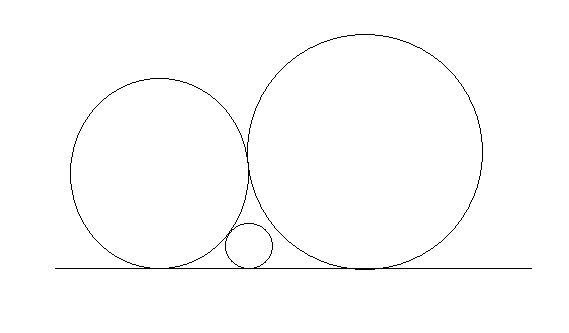
所以要从左 往右枚举第j=1~i-1个圆,判断j与i相切是否合理
合理是指:
第i个圆一定不与第1~i-1个圆相交
第i个圆的坐标一定大于第i-1个圆的坐标
2)
有可能出现第i个圆的坐标x大于其半径r的情况,这时要使第i个圆与直线x=0相切
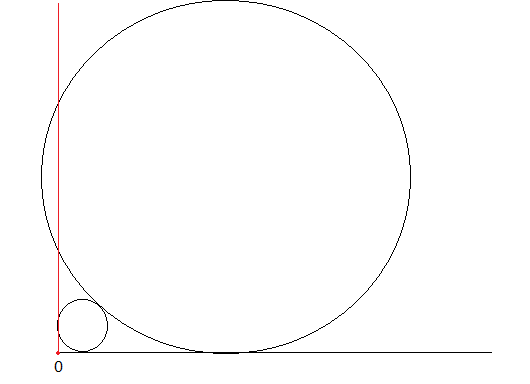
AC代码:
#include <iostream> #include<cstdio> #include<cmath> #include<cstring> #define inf 0x3f3f3f3f using namespace std; int n,vis[10]; double r[10],ans; struct Point{ double x,y; }point[10]; double get_dis(Point a,Point b){ return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } void dfs(int cur,double len){ if(cur==n+1){ //for(int i=1;i<=n;i++) printf("%.3f ",point[i].x);printf(" "); ans=min(ans,len); return; } for(int i=1;i<=n;i++){ if(vis[i]) continue; vis[i]=1; if(cur==1) point[cur].x=point[cur].y=r[i]; else{ for(int j=1;j<=cur-1;j++){ double L=sqrt((point[j].y+r[i])*(point[j].y+r[i])-(point[j].y-r[i])*(point[j].y-r[i])); Point tmp=Point{point[j].x+L,r[i]}; if(tmp.x<point[cur-1].x) continue; bool flag=true; for(int k=1;k<=cur-1;k++){ if(k==j) continue; if(get_dis(point[k],tmp)<point[k].y+r[i]) {flag=0;break;} } if(flag){ if(tmp.x<r[i]) point[cur].x=point[cur].y=r[i]; else point[cur]=tmp; break; } } } dfs(cur+1,max(len,point[cur].x+r[i])); vis[i]=0; } } int main() { int t;scanf("%d",&t); while(t--){ scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%lf",&r[i]); ans=inf; memset(vis,0,sizeof(vis)); dfs(1,0); printf("%.3f ",ans); } return 0; }