问题 G: 约数研究
时间限制: 1 Sec 内存限制: 128 MB提交: 30 解决: 25
[提交] [状态] [讨论版] [命题人:admin]
题目描述
科学家们在Samuel星球上的探险得到了丰富的能源储备,这使得空间站中大型计算机“Samuel II”的长时间运算成为了可能。由于在去年一年的辛苦工作取得了不错的成绩,小联被允许用“Samuel II”进行数学研究。
小联最近在研究和约数有关的问题,他统计每个正数N的约数的个数,并以f(N)来表示。例如12的约数有1、2、3、4、6、12。因此f(12)=6。下表给出了一些f(N)的取值:

现在小联希望用“Samuel II”来统计f(1)到f(N)的累加和M。
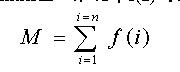
小联最近在研究和约数有关的问题,他统计每个正数N的约数的个数,并以f(N)来表示。例如12的约数有1、2、3、4、6、12。因此f(12)=6。下表给出了一些f(N)的取值:

现在小联希望用“Samuel II”来统计f(1)到f(N)的累加和M。
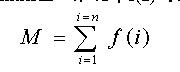
输入
只有一行一个整数 N(0 < N < 1000000)
输出
只有一行输出,为整数M,即f(1)到f(N)的累加和。
样例输入
3
样例输出
5
思路:
1.打表找规律:f[x]=∏(num_of{prime_fac[i]}+1)
2.约数i对答案的贡献为N/i ans=sum(N/i)
AC代码:
#include <iostream> #include<cstdio> #include<cmath> typedef long long ll; using namespace std; bool isprime[1000010]; ll cnt=0,prime[1000010]; ll num[1000010]; void get_prime(){ for(int i=0;i<=1000000;i++) isprime[i]=1; isprime[0]=isprime[1]=0; for(ll i=2;i<=1000000;i++){ if(isprime[i]) { prime[++cnt]=i;num[i]=2; for(ll j=i+i;j<=1000000;j+=i) { isprime[j]=0; ll tmp=0,cop=j; while(cop%i==0) cop/=i,tmp++; num[j]*=(tmp+1); } } } } int main() { for(ll i=0;i<=1000000;i++) num[i]=1; get_prime(); ll n;scanf("%lld",&n); ll ans=0; for(ll i=1;i<=n;i++){ ans+=num[i]; } printf("%lld ",ans); return 0; }
问题 D: 洗牌
时间限制: 1 Sec 内存限制: 128 MB提交: 18 解决: 14
[提交] [状态] [讨论版] [命题人:admin]
题目描述
为了表彰小联为Samuel星球的探险所做出的贡献,小联被邀请参加Samuel星球近距离载人探险活动。 由于Samuel星球相当遥远,科学家们要在飞船中度过相当长的一段时间,小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后,大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。 对于扑克牌的一次洗牌是这样定义的,将一叠N(N为偶数)张扑克牌平均分成上下两叠,取下面一叠的第一张作为新的一叠的第一张,然后取上面一叠的第一张作为新的一叠的第二张,再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。 如果对一叠6张的扑克牌1 2 3 4 5 6,进行一次洗牌的过程如下图所示:

从图中可以看出经过一次洗牌,序列1 2 3 4 5 6变为4 1 5 2 6 3。当然,再对得到的序列进行一次洗牌,又会变为2 4 6 1 3 5。 游戏是这样的,如果给定长度为N的一叠扑克牌,并且牌面大小从1开始连续增加到N(不考虑花色),对这样的一叠扑克牌,进行M次洗牌。最先说出经过洗牌后的扑克牌序列中第L张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利,你能帮助他吗?

从图中可以看出经过一次洗牌,序列1 2 3 4 5 6变为4 1 5 2 6 3。当然,再对得到的序列进行一次洗牌,又会变为2 4 6 1 3 5。 游戏是这样的,如果给定长度为N的一叠扑克牌,并且牌面大小从1开始连续增加到N(不考虑花色),对这样的一叠扑克牌,进行M次洗牌。最先说出经过洗牌后的扑克牌序列中第L张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利,你能帮助他吗?
输入
有三个用空格间隔的整数,分别表示N,M,L (其中0< N ≤ 10 ^ 10 ,0 ≤ M ≤ 10^ 10,且N为偶数)。
输出
单行输出指定的扑克牌的牌面大小。
样例输入
6 2 3
样例输出
6
思路:找规律:
N=12时,变化关系为
1->2->4->8->3->6->12->11->9->5->10->7->1
(i->j表示经一次洗牌后位置i移动到了位置j)
可见经1次洗牌后位置x移动到了x*2%(N+1)
所以经M次洗牌后位置x将移动到x*pow(2,M)%(N+1)
已知位置x移动M次后至位置L,求位置x
即求方程x*pow(2,M)%(N+1)=L的解x
AC代码:
#include <iostream> #include<cstdio> typedef long long ll; using namespace std; ll qpow(ll a,ll b,ll mod){ ll ret=1; while(b){ if(b&1) ret=ret*a%mod; a=a*a%mod; b>>=1; } return ret; } void exgcd(ll a,ll b,ll& d,ll& x,ll& y){ if(!b){ d=a; x=1; y=0;} else{ exgcd(b,a%b,d,y,x); y-=x*(a/b); } } int main() { ll n,m,l; scanf("%lld%lld%lld",&n,&m,&l); if(n==1) {printf("1 "); return 0;} ll a=qpow(2,m,n+1); ll b=(n+1); //printf("a=%lld b=%lld ",a,b); ll d,x,y; exgcd(a,b,d,x,y); x=x*(l/d),y=y*(l/d); //printf("x=%lld y=%lld ",x,y); ll k=b/d; //printf("%lld ",k); if(x<=0) x=x+(x/k)*k; if(x>n) x=x-((x-n)/k)*k; while(x<=0) x+=k; while(x>n) x-=k; printf("%lld ",x); return 0; }
问题 M: 分金币
时间限制: 1 Sec 内存限制: 128 MB提交: 118 解决: 44
[提交] [状态] [讨论版] [命题人:admin]
题目描述
圆桌上坐着n个人,每人有一定数量的金币,金币总数能被n整除。每个人可以给他左右相邻的人一些金币,最终使得每个人的金币数目相等。你的任务是求出被转手的金币数量的最小值。
输入
第一行为整数n(n>=3),以下n行每行一个正整数,按逆时针顺序给出每个人拥有的金币数。
3<=N<=100000,总金币数<=10^9
3<=N<=100000,总金币数<=10^9
输出
输出被转手金币数量的最小值
样例输入
4
1
2
5
4
样例输出
4
提示
设四个人编号为1,2,3,4。第3个人给第2个人2个金币(变成1,4,3,4),第2个人和第4个人分别给第1个人1个金币。
思路:
设xi表示i->i+1的金币(即i+1->i的金币为-xi)
则
a1+xn-x1=ave;
a2+x1-x2=ave;
...
an+xn-1-xn=ave;
所以:
x1=a1-ave+xn;
x2=a1+a2-2*ave+xn;
x3=a1+a2+a3-3*ave+xn;
...
xn-1=a1+a2+..+an-1-(n-1)*ave+xn;
所以min{|x1|+|x2|+|x3|+...+|xn|}=min{|ave-a1-xn|+|2*ave-a1-a2-xn|+...+|(n-1)*ave-a1-a2-..-an-1-xn|+|0-xn|}
AC代码:
#include <iostream> #include<cstdio> #include<cmath> #include<algorithm> typedef long long ll; using namespace std; ll a[100005],c[100005]; int main() { ll n;scanf("%lld",&n); ll sum=0; for(ll i=1;i<=n;i++){ scanf("%lld",&a[i]); sum+=a[i]; } ll ave=sum/n; for(ll i=1;i<=n-1;i++){ c[i]=c[i-1]+(ave-a[i]); } c[n]=0; sort(c+1,c+1+n); ll x=c[(n+1)/2]; ll ans=0; for(int i=1;i<=n;i++){ ans+=abs(c[i]-x); } printf("%lld ",ans); return 0; }