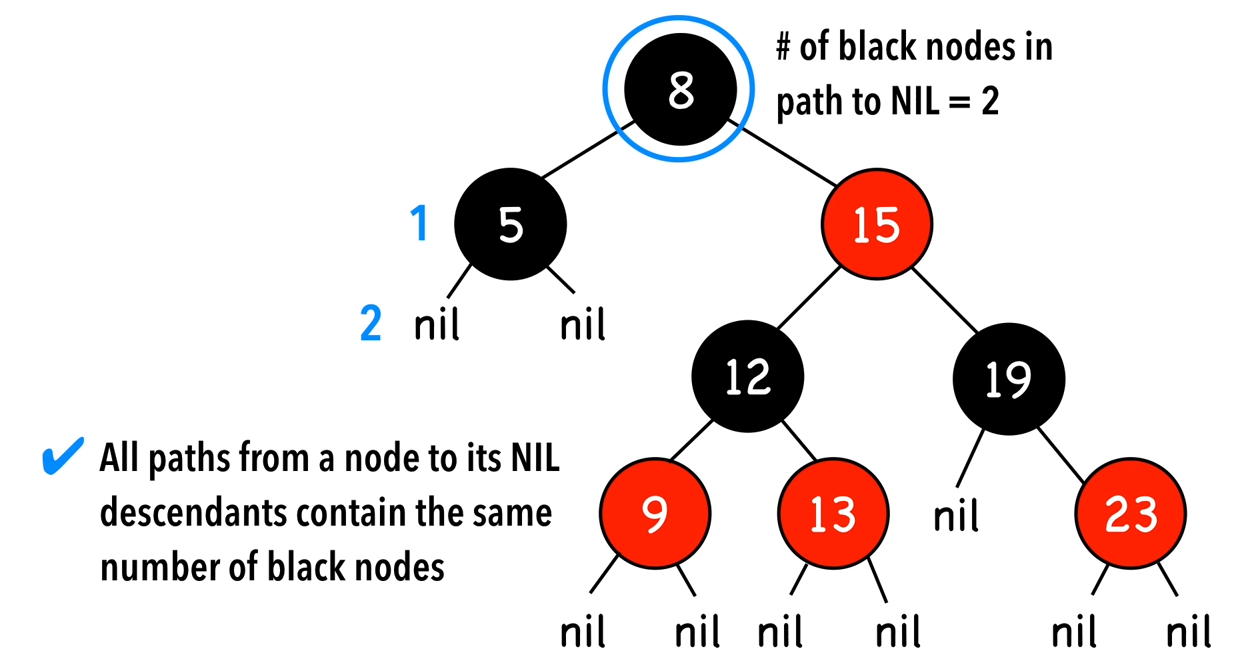
1) Every node has a color either red or black.
2) Root of tree is always black.
3) There are no two adjacent red nodes (A red node cannot have a red parent or red child).
4) Every path from a node (including root) to any of its descendant NULL node has the same number of black nodes.
Why Red-Black Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed(偏斜的) Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of a Red-Black tree is always O(Logn) where n is the number of nodes in the tree.
Comparison with AVL Tree
The AVL trees are more balanced compared to Red-Black Trees, but they may cause more rotations during insertion and deletion. So if your application involves many frequent insertions and deletions, then Red Black trees should be preferred. And if the insertions and deletions are less frequent and search is a more frequent operation, then AVL tree should be preferred over Red-Black Tree.
In AVL tree insertion, we used rotation as a tool to do balancing after insertion caused imbalance. In Red-Black tree, we use two tools to do balancing.
1) Recoloring
2) Rotation
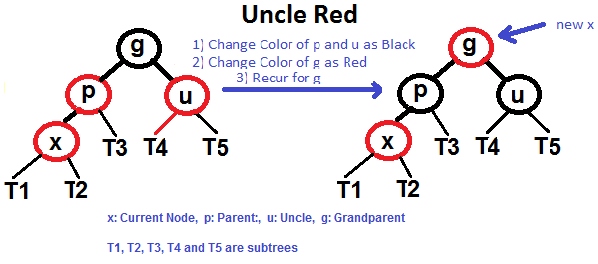
We try recoloring first, if recoloring doesn’t work, then we go for rotation. Following is detailed algorithm. The algorithms has mainly two cases depending upon the color of uncle. If uncle is red, we do recoloring. If uncle is black, we do rotations and/or recoloring.
Insertion:
Case:Uncle Red
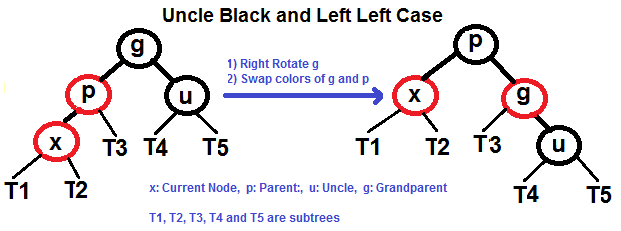
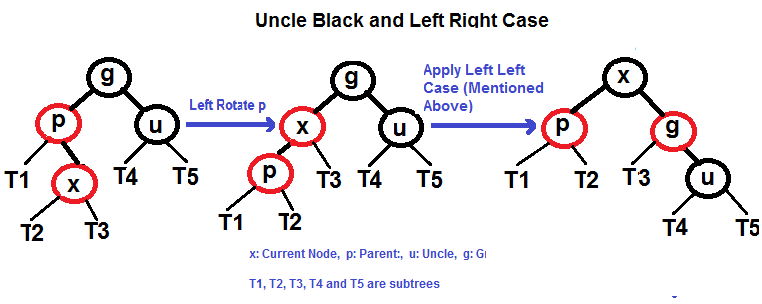
All four cases when Uncle is BLACK
Left Left Case (See g, p and x)
Left Right Case (See g, p and x)
Right Right Case (See g, p and x)
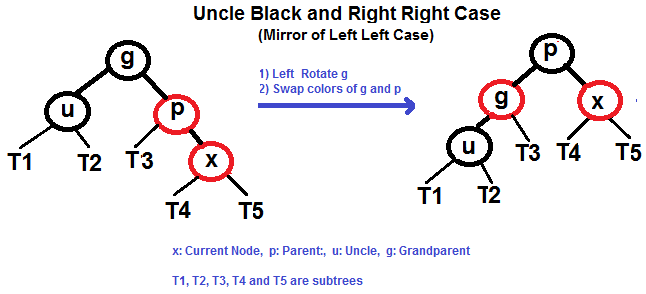
Right Left Case (See g, p and x)
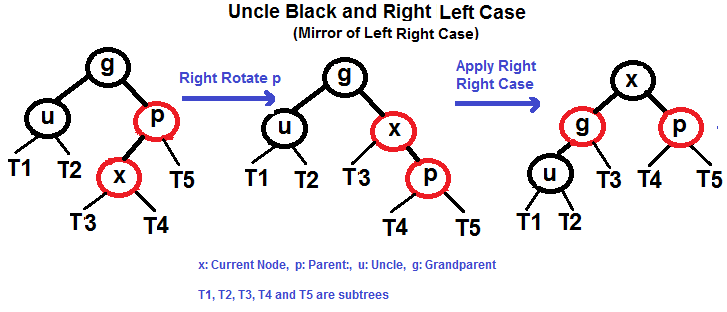
In insert operation, we check color of uncle to decide the appropriate case. In delete operation, we check color of sibling to decide the appropriate case.
Application: treeset and treemap in java
https://www.geeksforgeeks.org/red-black-tree-set-2-insert/
https://www.geeksforgeeks.org/red-black-tree-set-3-delete-2/