题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1695
题意:给你a,b,c,d,k。问你对于1<=x<=b,1<=y<=d。有多少对(x,y)使gcd(x,y) = k。其中(5,7)和(7,5)算一对。
问题转换:gcd(x,y) = k =》 gcd(x/k,y/k) = 1 ,转化之后就是求[1,b/k],[1,d/k]之间互质的数的对数
虽然懵逼乌斯反演基本不会,但还是要写一写。
第一种式子:
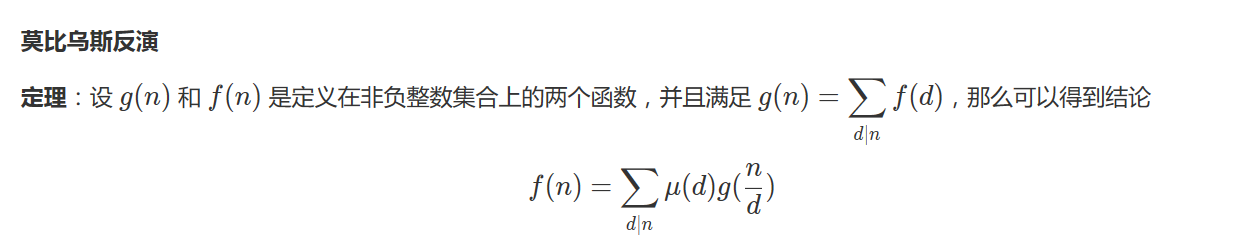
第二种式子:
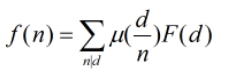
我们用的第二种式子,首先使用这个式子的条件是f(n)和F(n)的倍数关系,比如说在本题中,f(n)表示gcd(x,y)=n的对数,F(d)则表示gcd(x,y)=D(D是满足D%d==0的任意数)的对数
接着,把这个式子展开,就是f(n)=u(1)F(1*n)+u(2)F(2*n)+u(3)F(3*n)+...u(1)F(i*n)+..
而这题为什么要用第二种莫比乌斯反演呢,是因为这题的f(n)难求,而F(n)很好知道,F(n)=(b/n)*(d/n),所以求出本题只需要先预处理出莫比乌斯函数u(x),然后下面的循环:
for(i = 1; i <= d;i++)
sum1 += (ll)mu[i]*(b/i)*(d/i);
当然还得去重,具体看下面的代码

1 #include<stdio.h>
2 #include<string.h>
3 #define MAXN 1000000
4 int check[MAXN+10];
5 int prime[MAXN+10];
6 int mu[MAXN+10];
7 typedef long long ll;
8 void Moblus()
9 {
10 memset(check,0,sizeof(check));
11 mu[1] = 1;
12 int tot = 0,i,j;
13 for(i = 2; i <= MAXN; i++)
14 {
15 if( !check[i] )
16 {
17 prime[tot++] = i;
18 mu[i] = -1;
19 }
20 for(j = 0; j < tot; j++)
21 {
22 if(i * prime[j] > MAXN) break;
23 check[i * prime[j]] = 1;
24 if( i % prime[j] == 0)
25 {
26 mu[i * prime[j]] = 0;
27 break;
28 }
29 else
30 {
31 mu[i * prime[j]] = -mu[i];
32 }
33 }
34 }
35 }
36
37 int main()
38 {
39 int T,a,b,c,d,k,t,id=1,i;
40 ll sum1,sum2;
41 scanf("%d",&T);
42 Moblus();
43 while(T--)
44 {
45 sum1=0,sum2=0;
46
47 scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
48 if(k==0)
49 {
50 printf("Case %d: 0
",id++);
51 continue;
52 }
53
54 b=b/k,d=d/k;
55 if(b<d) t=b,b=d,d=t;
56
57 for(i = 1; i <= d;i++)
58 sum1 += (ll)mu[i]*(b/i)*(d/i);
59
60 for(i = 1;i <= d;i++)
61 sum2 += (ll)mu[i]*(d/i)*(d/i);
62
63 sum1 -= sum2/2;
64 printf("Case %d: %lld
",id++,sum1);
65 }
66 return 0;
67 }
第二种方法:
转化成求互质对数后,枚举x(保证x>y就不会重复),用欧拉函数和容斥定理不会超时
