后缀数组是一种处理字符串的算法。
它可以将所有后缀按字典序排序,并求出任意2个后缀的最长公共前缀。
首先将所有后缀排序,因为后缀有这样的性质:任意一个后缀都可以拆分成另一个后缀和一个子串,且一个子串也可以拆分成其他子串,所以可以采用倍增算法对所有后缀进行排序,方法如下:(分若干步)
第k步的处理如下:
首先,根据上一步的结果,得到每个位置开始,长度为(2^{k-1})的子串的排名。
然后,把长度为(2^{k-1})的子串拼在一起,得到长度为(2^{k})的子串。
通过之前的排名,将长度为(2^{k-1})的子串,变为一个数字(原理类似离散化)。
这样,长度为(2^{k})的的子串,就变成了两个数字。
这样,通过排序,就能求出从每个位置开始,长度为(2^{k})的子串的排名。
如下图:
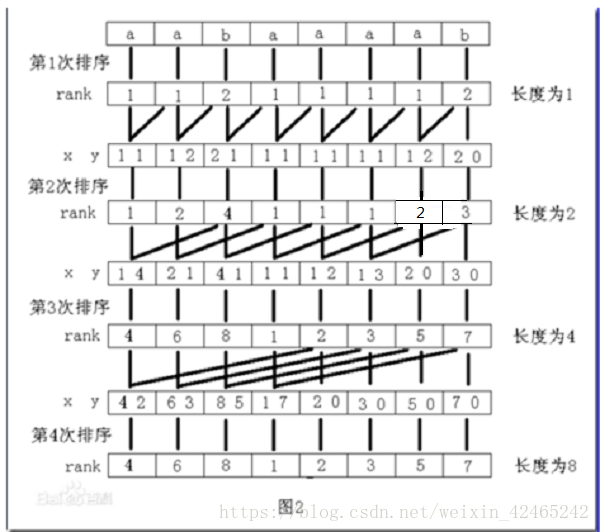
因为需要排序的数字的最大值不会超过n,所以可以采用基数排序,时间复杂度(O(nlogn))
后缀数组代码:
#include <stdio.h>
#include <string.h>
char zf[1000010];
int js[1000010]={0};
int x[1000010],y[1000010];
int sa[1000010];
int main()
{
scanf("%s",zf);
int n,m;
for(n=0;zf[n]!=0;n++)
js[x[n]=zf[n]]+=1;//基数排序,同时求出字符串长度
for(int i='0';i<='z';i++)
js[i]+=js[i-1];;//基数排序,求前缀和
for(int i=n-1;i>=0;i--)
sa[--js[x[i]]]=i;//放回数组
m='z';
for(int mi=1;mi<=n;mi=(mi<<1))
{
int s=0;
for(int i=n-mi;i<n;i++)
y[s++]=i;//处理出第二关键字为空的位置
for(int i=0;i<n;i++)//从小到大,枚举第二关键字的位置
{
if(sa[i]>=mi)//此位置存在对应的第一关键字
y[s++]=sa[i]-mi;//保存位置
}
//此时,y中储存的是按照第二关键字从小到大排序后,第一关键字的位置
for(int i=1;i<=m;i++)
js[i]=0;
for(int i=0;i<n;i++)
js[x[i]]+=1;
for(int i=1;i<=m;i++)
js[i]+=js[i-1];
for(int i=n-1;i>=0;i--)
sa[--js[x[y[i]]]]=y[i];
//对第一关键字进行基数排序
m=1;
y[sa[0]]=1;
for(int i=1;i<n;i++)
{
if(x[sa[i]]!=x[sa[i-1]]||x[sa[i]+mi]!=x[sa[i-1]+mi])//与上一个不相同
m+=1;
y[sa[i]]=m;
}
//处理排名
if(m==n)//所有排名都出现过,算法结束
break;
for(int i=0;i<n;i++)//将排名赋值回原来的数组
x[i]=y[i];
}
for(int i=0;i<n;i++)
printf("%d ",sa[i]+1);
return 0;
}
height数组:
很多时候,只有一个sa数组,能做的事情并不多,我们通常还需要一个height数组,表示排名相邻的两个后缀的最长公共前缀。
暴力求是(O(n^2))的。
考虑优化:
设h(i)表示从i开始的后缀和它上一排名的最长公共前缀。
有如下结论成立:(h(i+1)geq h(i)-1)
证明:
分两种情况:
- h(i)>0,设i的上一排名为j,说明后缀i的第一个字符和后缀j的第一个字符相等,后缀j<后缀i,所以后缀j+1<后缀i+1(就是都去掉第一个字符后仍然小于)。后缀j+1和后缀i+1的最长公共前缀长度是h(i)-1,并且在同大于或小于的i情况下,排名越接近,h越大。所以h(i+1)至少是h(i)-1。
- h(i)=0。此时,h(i)-1为-1。由于h一定为非负整数,所以h(i+1)一定>-1。
证明完毕。
然后,通过height数组,还可以求得任意两个后缀的最长公共前缀。
如下图:
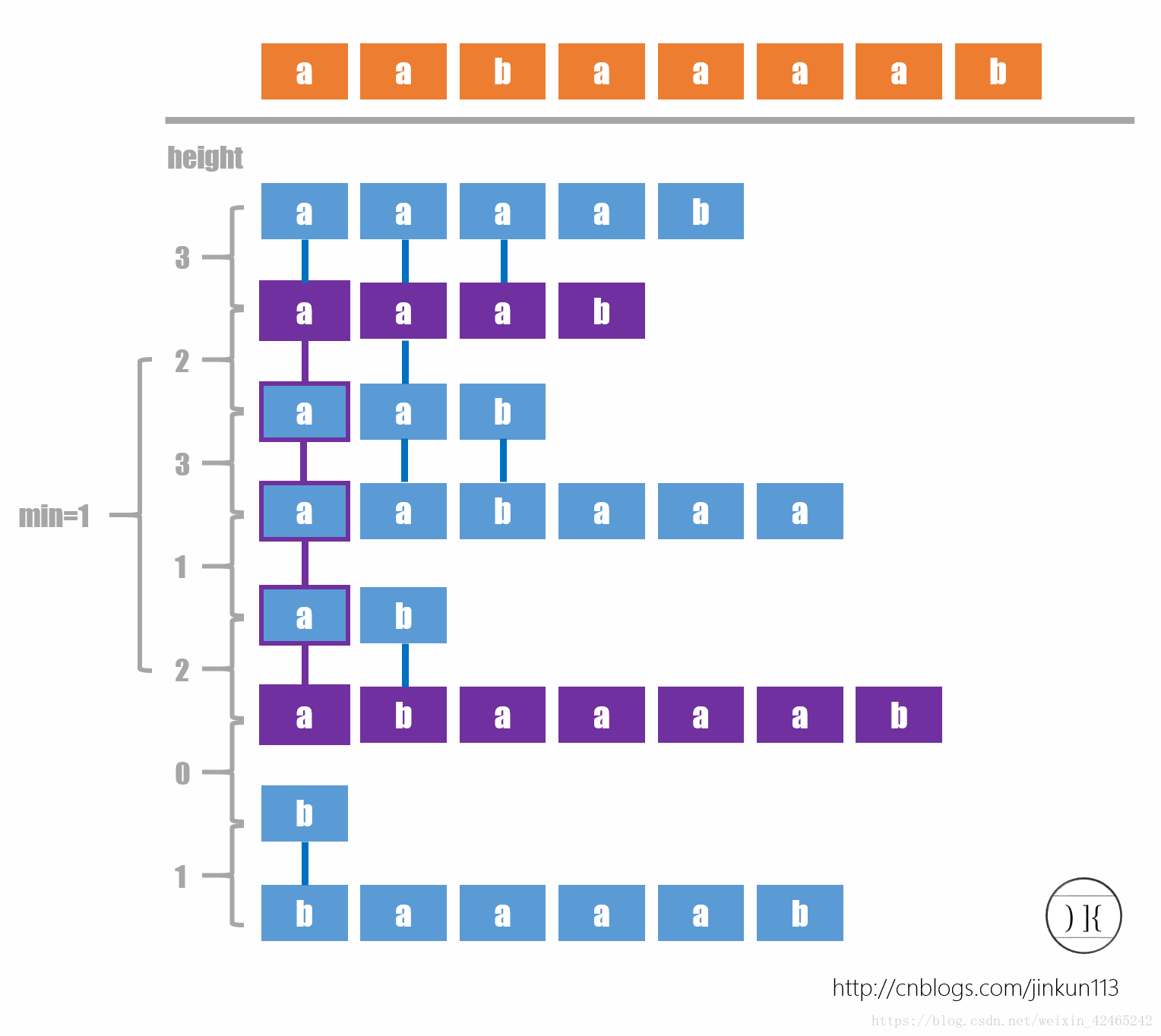
就是从i到j,最大的变化。
就是求(RMQ(h(ra[a]+1),h(ra[b])))
代码:
for(int i=0,h=0;i<n;i++)
{
if(ra[i]==0)
continue;
if(h>0)
h-=1;
int j=sa[ra[i]-1];
while(zf[i+h]==zf[j+h])
h+=1;
hei[ra[i]]=h;
}
例题:
NOI2016优秀的拆分
枚举长度L,然后放置关键点,求相邻关键点的lcp,lcs,然后差分。
复杂度(O(nlogn))。
代码:
#include <stdio.h>
#include <string.h>
#define ll long long
int lo[30010],N;
char ch[30010];
int cf1[30010],cf2[30010];
struct SA
{
int sa[30010],x[60010],y[30010],sl[30010],ra[30010],hei[30010],zx[15][30010];
char zf[30010];
void getsa(int n)
{
zf[n]=0;
for(int i=0;i<=n+n;i++)
x[i]=0;
for(int i=0;i<='z';i++)
sl[i]=0;
for(int i=0;i<n;i++)
sl[x[i]=zf[i]]+=1;
for(int i=1;i<='z';i++)
sl[i]+=sl[i-1];
for(int i=n-1;i>=0;i--)
sa[--sl[x[i]]]=i;
int m='z';
for(int mi=1;mi<=n;mi*=2)
{
int s=0;
for(int i=n-mi;i<n;i++)
y[s++]=i;
for(int i=0;i<n;i++)
{
if(sa[i]>=mi)
y[s++]=sa[i]-mi;
}
for(int i=1;i<=m;i++)
sl[i]=0;
for(int i=0;i<n;i++)
sl[x[i]]+=1;
for(int i=1;i<=m;i++)
sl[i]+=sl[i-1];
for(int i=n-1;i>=0;i--)
sa[--sl[x[y[i]]]]=y[i];
m=1;
for(int i=0;i<n;i++)
{
if(i!=0&&(x[sa[i]]!=x[sa[i-1]]||x[sa[i]+mi]!=x[sa[i-1]+mi]))
m+=1;
y[sa[i]]=m;
}
if(m==n)
break;
for(int i=0;i<n;i++)
x[i]=y[i];
}
for(int i=0;i<n;i++)
ra[sa[i]]=i;
for(int i=0,h=0;i<n;i++)
{
if(ra[i]==0)
continue;
if(h>0)
h-=1;
int j=sa[ra[i]-1];
while(zf[i+h]==zf[j+h])
h+=1;
hei[ra[i]]=h;
}
for(int i=1;i<n;i++)
zx[0][i]=hei[i];
for(int i=1;i<=lo[n];i++)
{
for(int j=1;j<n;j++)
{
if(j+(1<<i)-1>=n)
break;
zx[i][j]=zx[i-1][j+(1<<(i-1))];
if(zx[i-1][j]<zx[i][j])
zx[i][j]=zx[i-1][j];
}
}
}
int RMQ(int l,int r)
{
int i=lo[r-l+1];
int jg=zx[i][r-(1<<i)+1];
if(zx[i][l]<jg)
jg=zx[i][l];
return jg;
}
};
SA ch1,ch2;
int getlcp(int a,int b)
{
if(ch1.ra[a]>ch1.ra[b])
{
int t=a;
a=b;
b=t;
}
return ch1.RMQ(ch1.ra[a]+1,ch1.ra[b]);
}
int getlcs(int a,int b)
{
a=N-1-a;
b=N-1-b;
if(ch2.ra[a]>ch2.ra[b])
{
int t=a;
a=b;
b=t;
}
return ch2.RMQ(ch2.ra[a]+1,ch2.ra[b]);
}
void yucl()
{
lo[1]=0;
for(int i=2;i<=N;i++)
lo[i]=lo[i>>1]+1;
ch1.getsa(N);
ch2.getsa(N);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%s",ch);
N=strlen(ch);
for(int i=0;i<N;i++)
{
ch1.zf[i]=ch2.zf[N-1-i]=ch[i];
cf1[i]=cf2[i]=0;
}
yucl();
for(int l=1;l<=N;l++)
{
for(int i=0;i+l<N;i+=l)
{
int j=i+l;
int x=getlcp(i,j),y=getlcs(i,j);
if(x>l)
x=l;
if(y>l)
y=l;
if(x+y>l)
{
int L=i+1-y,R=i+x-l;
cf1[L]+=1;
cf1[R+1]-=1;
cf2[L+l+l]+=1;
cf2[R+l+l+1]-=1;
}
}
}
ll jg=0;
int he1=0,he2=0;
for(int i=0;i<N;i++)
{
he1+=cf1[i];
he2+=cf2[i];
jg+=(ll)he1*he2;
}
printf("%lld
",jg);
}
return 0;
}
应用:
- 二分/枚举长度,然后划分为若干区间
- 统计问题可以转化为RMQ之和,可以枚举最小值,然后单调栈
- 循环串,连续重复串可以枚举长度,然后放置关键点,使用lcp+lcs等。