---恢复内容开始---
一、与K-mean算法的比较:

二、Gauss Mixture 模型
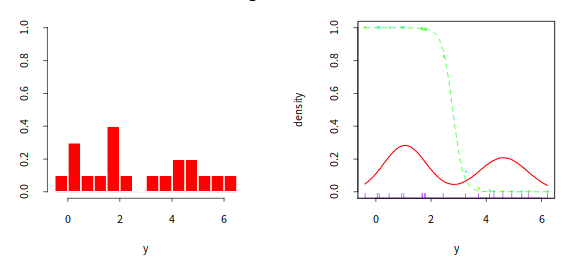

- 有一组数据,直方图如左上。显然这样的分布不能用某一个单峰简单分布来描述,可以利用高斯混合分布来解决。
分布Y由两个高斯分布混合而成:
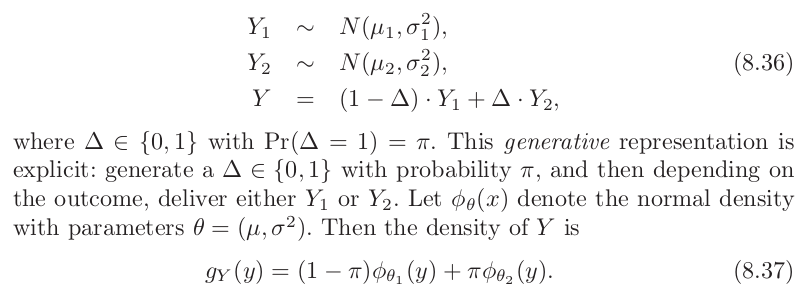
- 现在,我们要求未知参数
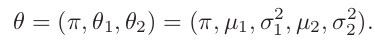
- 那么似然函数是这样的(基于N个已知数据的对数似然)
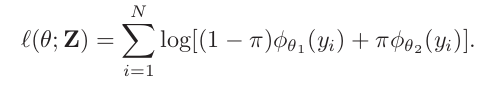
- 由于这个似然函数很难求得使似然最大的参数,因此,引入前面提到的潜变量∆ ,但是∆的值实际上未知,我们用其期望来替代,期望是未知参数的函数,这个期望称作responsibility:

三、EM算法
- 通过EM算法来求得参数,这事实上是一种聚类。
- 随机选择参数开始
- 计算∆的期望γ
- 利用γ计算各参数
- 。。。反复迭代直到参数不再更新

关于开始参数的选择:
