Today Pari and Arya are playing a game called Remainders.
Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 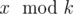 . There are n ancient numbers c1, c2, ..., cn and Pari has to tell Arya
. There are n ancient numbers c1, c2, ..., cn and Pari has to tell Arya 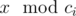 if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value
if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value 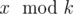 for any positive integer x?
for any positive integer x?
Note, that 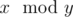 means the remainder of x after dividing it by y.
means the remainder of x after dividing it by y.
The first line of the input contains two integers n and k (1 ≤ n, k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.
The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 1 000 000).
Print "Yes" (without quotes) if Arya has a winning strategy independent of value of x, or "No" (without quotes) otherwise.
4 5
2 3 5 12
Yes
2 7
2 3
No
In the first sample, Arya can understand 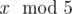 because 5 is one of the ancient numbers.
because 5 is one of the ancient numbers.
In the second sample, Arya can't be sure what 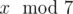 is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.
is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.
#include <cstdio> #include <cmath> #include <cstring> #include <algorithm> #include <map> #include <iostream> using namespace std; #define ll long long ll lcm; const int maxn = 1e6 + 10; ll getlcm(ll a, ll b) { return a / __gcd(a, b) * b; } ll p[maxn]; int main() { ll n, k; while(~scanf("%I64d %I64d", &n, &k)) { for(int i = 1; i <= n; i++) scanf("%I64d", &p[i]); ll lcm = 1; int flag = 0; for(int i = 1; i <= n; i++) { lcm = getlcm(lcm, p[i]); lcm = lcm % k; if(lcm == 0) { puts("Yes"); flag = 1; break; } } if(!flag) puts("No"); } }