Codeforces Round #365 (Div. 2) D. Mishka and Interesting sum (树状数组 + 离线查询)

D. Mishka and Interesting sum

Little Mishka enjoys programming. Since her birthday has just passed, her friends decided to present her with array of non-negative integers a1, a2, ..., an of n elements!

Mishka loved the array and she instantly decided to determine its beauty value, but she is too little and can't process large arrays. Right because of that she invited you to visit her and asked you to process m queries.

Each query is processed in the following way:

1. Two integers l and r (1 ≤ l ≤ r ≤ n) are specified — bounds of query segment.
2. Integers, presented in array segment [l,  r] (in sequence of integers al, al + 1, ..., ar) even number of times, are written down.
3. XOR-sum of written down integers is calculated, and this value is the answer for a query. Formally, if integers written down in point 2 are x1, x2, ..., xk, then Mishka wants to know the value , where  — operator of exclusive bitwise OR.

Since only the little bears know the definition of array beauty, all you are to do is to answer each of queries presented.

Input

The first line of the input contains single integer n (1 ≤ n ≤ 1 000 000) — the number of elements in the array.

The second line of the input contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — array elements.

The third line of the input contains single integer m (1 ≤ m ≤ 1 000 000) — the number of queries.

Each of the next m lines describes corresponding query by a pair of integers l and r (1 ≤ l ≤ r ≤ n) — the bounds of query segment.

Output

Print m non-negative integers — the answers for the queries in the order they appear in the input.

Examples

input

3
3 7 8
1
1 3

output

0

input

7
1 2 1 3 3 2 3
5
4 7
4 5
1 3
1 7
1 5

output

0
3
1
3
2

Note

In the second sample:

There is no integers in the segment of the first query, presented even number of times in the segment — the answer is 0.

In the second query there is only integer 3 is presented even number of times — the answer is 3.

In the third query only integer 1 is written down — the answer is 1.

In the fourth query all array elements are considered. Only 1 and 2 are presented there even number of times. The answer is .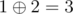

In the fifth query 1 and 3 are written down. The answer is .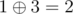

题意是求区间内出现偶数次的数的异或和，根据异或的概念，异或奇数次的数再异或一次这个数就变成0了，异或偶数次的数再异或这个数就变成自身了，所以题目就变成了区间所有数的异或和再异或一次区间中不同的数的异或和(类似hdu3333的离线查询, 不过是加法变成异或)，可以用树状数组解决。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 10;
int n;
int a[maxn];
int Xsum[maxn];
int c[maxn];
struct node {
    int l, r, ans, id;
}p[maxn];

bool cmp1(node a, node b) {
    return a.r < b.r;
}

bool cmp2(node a, node b) {
    return a.id < b.id;
} 

inline int lowbit(int x) {
    return x & (-x);
}

int sum(int x) {
    int ret = 0;
    while(x > 0) {
        ret ^= c[x]; x -= lowbit(x);
    }
    return ret;
}

void add(int x, int d) {
    while(x <= n) {
        c[x] ^= d; x += lowbit(x);
    }
}

int main()  {
    Xsum[0] = 0;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        Xsum[i] = Xsum[i-1] ^ a[i];
    }
    int m;
    scanf("%d", &m);
    for(int i = 1; i <= m; i++) {
        scanf("%d %d", &p[i].l, &p[i].r);
        p[i].id = i;
    }
    memset(c, 0, sizeof(c));
    sort(p + 1, p + 1 + m, cmp1);
    int pos = 1;
    map<int, int> mp;
    for(int i = 1; i <= n; i++) {
        if(mp[a[i]]) {
            add(mp[a[i]], a[i]);
            a[mp[a[i]]] = 0;
        }
        mp[a[i]] = i;
        add(i, a[i]);
        for( ; pos <= m && i == p[pos].r; pos++) {
            p[pos].ans = Xsum[p[pos].r] ^ Xsum[p[pos].l-1] ^ sum(p[pos].r) ^ sum(p[pos].l-1);
        }
    }
    sort(p + 1, p + 1 + m, cmp2);
    for(int i = 1; i <= m; i++) {
        printf("%d
", p[i].ans);
    }
}