Minimum Snap轨迹规划详解（2）corridor与时间分配

在上一篇文章中，我们得到的轨迹并不是很好，与路径差别有点大，我们期望规划出的轨迹跟路径大致重合，而且不希望有打结的现象，而且希望轨迹中的速度和加速度不超过最大限幅值。为了解决这些问题有两种思路：

    思路一：把这些”期望“加入到优化问题中。
    思路二：调整时间分配，来避免这些问题。
1.corridor
1.1 corridor是什么？

为了限制轨迹的形状，引入了corridor的概念，corridor可以理解为可行通道，如下图，规划出的轨迹必须在corridor内。直观的思路是：如果能把corridor当作约束加入到QP问题中，那么解得的轨迹自然就在corridor内了。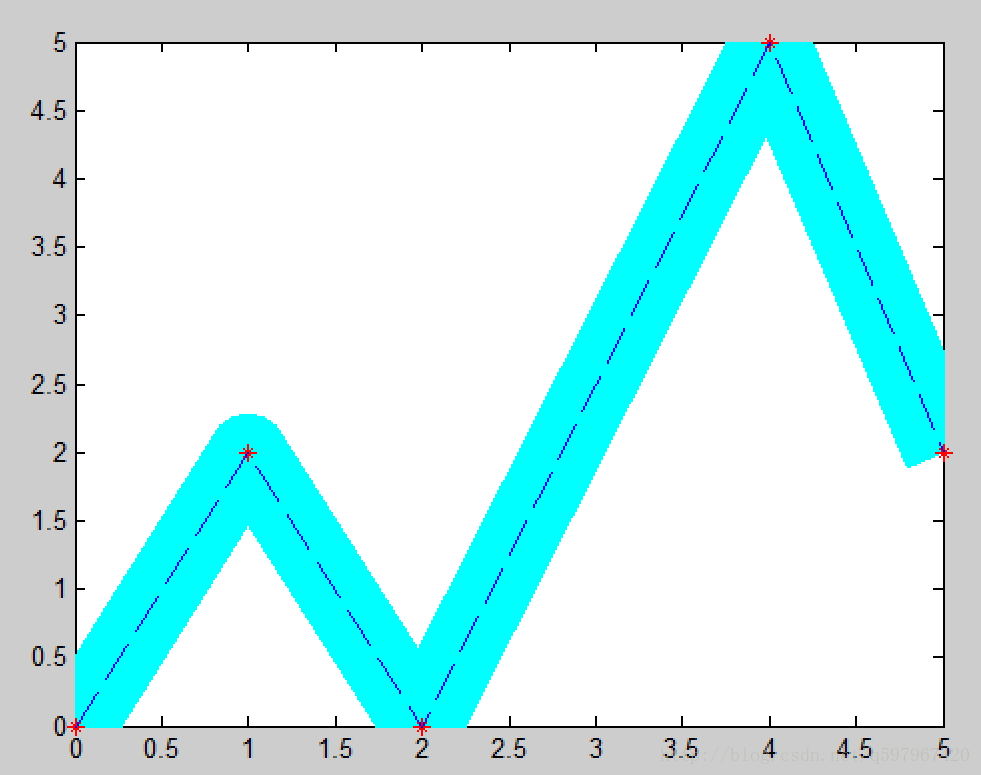

 1.2 corridor约束怎么加？

很容易想到，把之前的等式约束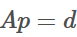改成不等式约束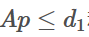和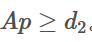。然而，不管是等式约束还是不等式约束，都是针对一个特定的时刻，而实际希望的是对所有时刻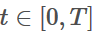

  ，都需要在corridor中。
一个简单粗暴的思路：在路径上多采样一些中间点，每个中间点都加corridor约束。尽管这种方法理论上只能保证采样点在corridor中，但实际过程中，如果corridor大小和采样步长设置得合理，而且不Fix waypoints，能work的比较好。这里不fix 中间点的位置，是为了去掉中间点的强约束，尽量避免轨迹打结，实际中，我们也是不一样要求轨迹完全经过中间点，只要在那附近（corridor）内就行。

1.3 构造corridor不等式约束

为了方便构造，对于每一个采样点pt，我们施加一个矩形的corridor，即

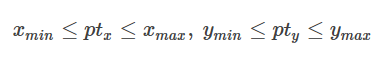
这里用矩形corridor是因为斜线corridor（平行四边形）不好构造，而且我们只需要大致在corridor里面就好，没有必要非弄一个严格的斜线corridor。对于每个采样点，设矩形corridor的边长为2r，增加两个位置不等式约束：

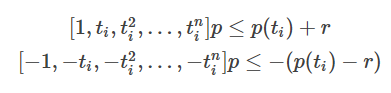
1.4 实验结果

代码见这里
优化列表in

• min：snap
• 等式约束：起点pva(3)+终点pva(3)+中间点pva连续(3*(n_ploy-1))
• 不等式约束：中间点位置corridor(2*(n_ploy-1))

优化结果如下图所示，绿色的点为按固定步长新采样的中间点，每个中间点都有一个矩形corridor，红色为优化后的轨迹。可以看到，去掉中间点的位置强约束(等式约束)改成弱约束(corridor不等式约束)后，轨迹比之前要好很多，而且尽管轨迹有小部分超出了corridor（因为只加了采样时刻的位置corridor约束），但基本不会超出太多。

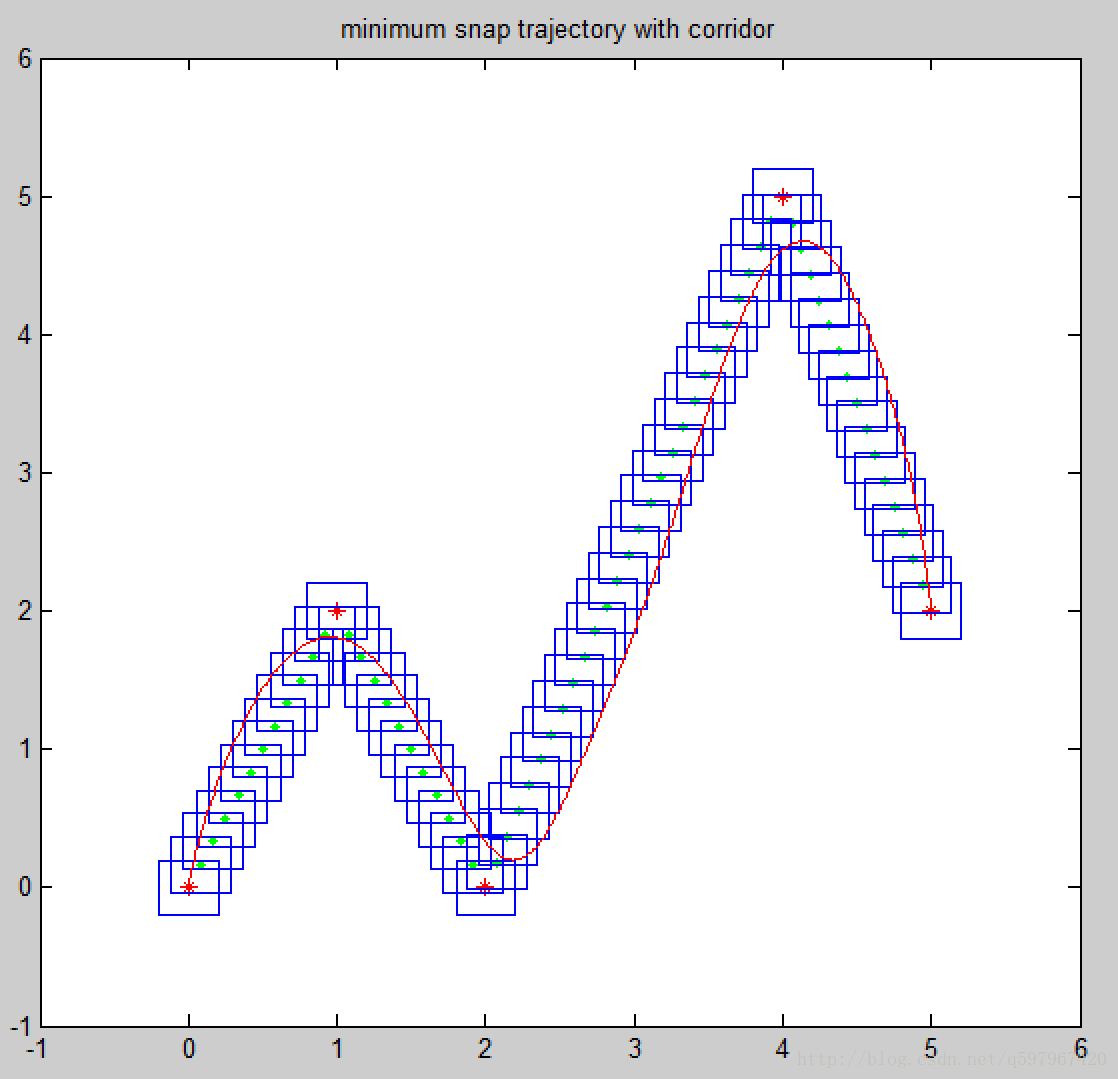
但这带来的一个问题是，为了保证轨迹不超出corridor，需要采样比较密，但这样轨迹的段数就上来的（轨迹段数=waypoint数量-1），优化参数变多了，计算效率会下降。

•     一种解决思路是通过corridor合并来减少中间点轨迹段数，从而提高计算效率；
•     另一种解决思路是，不采样中间点，直接规划出轨迹以后，找到轨迹的极值点（波峰、波谷），若极值点位置超出corridor，在极值点上添加一个corridor或者位置强约束（俗称”压点“，把极值点压到corridor以内），以此迭代。实验证明：压有限个（不超过路径点总数）点就能把整段轨迹压到corridor以内。

1.5 广义corridor

上面实验介绍了位置corridor，也就是位置不等式约束，但同样也可以扩展到速度corridor、加速度corridor乃至更高阶。
诶~是不是有点灵感？上一篇文章中实验得到的轨迹的另一个问题是速度、加速度超过了最大限幅，所以同样的思路每个waypoint都增加速度、加速度corridor，是不是就能解决了？
然而，并不能！！！ 为什么呢？举个简单的例子，假设一维空间规划一条轨迹从0到10，给定总时间T=1s，要求最大限速2m/s，满足要求的轨迹根本不存在，即使你加很多中间点并加速度corridor，得到的轨迹在采样点中间肯定会速度蹭的巨高。
速度、加速度之所以很大，是因为时间给的不合理（时间太小），所以这种情况光靠加corridor是行不通的，还是要从时间分配的层面来解决。
2. 时间分配
时间分配是轨迹规划中很关键的一个问题，它直接影响规划结果的好坏。
2.1 初始时间分配

    总时间给定：通常给一个平均速度，根据总路程计算得到总时间

    各段时间分配：
        匀速分配：假设每段polynomial内速度恒定不变，这样各段poly的时间比就等于路程比。
        梯形分配：假设每段polynomial内速度曲线为：以恒定加速度a从0加速到最大速度v_max，再以−a减速到0。a和v_max事先给定，就能得出每一段所需要的时间。

设各段时间分别为t′₁,t′₂,...,t′_n，求前k项和可以得到轨迹分段的时刻向量t₀=0,t₁=t′₁,t₂=t₁+t′₂,...,t_n=t_n−1+t′_n。

2.2 feasibility check

有了时间分配，就可以规划得到轨迹参数，对于轨迹参数，求速度和加速度曲线的极值，判断是否超过最大限幅，如果所有极值都小于最大限幅，则得到可行轨迹。如果不满足，则需要调整该段的时间。
调整的方法是：增大unfeasible段poly的时间，显然，增大时间会使得速度和加速度都变小。通常以一个固定的比例来调整时间如（k=1.2~1.5），并进行迭代，每调整一次，重新规划轨迹并check feasibility，如若不满足，再次加大时间，直至满足为止。
2.3 corridor与时间分配的关联

不等式corridor约束实际上也有时间分配的效果，可以这么想，polynomial的分段点（轨迹中间点）在corridor内移动，实际上就相当于分段点的时刻在移动，中间点在corridor内移动，也就变相调整了前后两段poly分配的时间。
举个简单的例子，如下图所示，

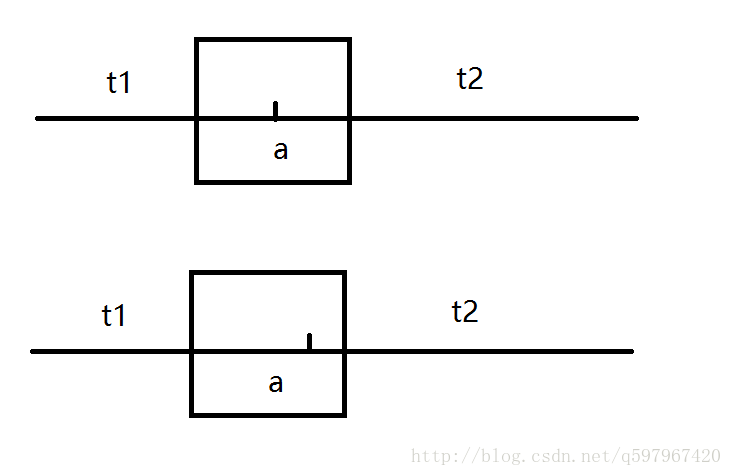
 两段轨迹的分段点为a，初始时间分配为t1,t2，比如说想减少前一段的时间t1，加大后一段的时间t2，其实就相当于把分段点a向右挪。也就是说，还是前段poly仍然分配t1时间，但走的路程更多了（相当于原来路程所用的时间减少了），后一段poly在t2时间走的路程更少了（相当于原来的路程所用时间增加了）。所以如果corridor比较大的话，时间调整的空间就会更大，规划出的轨迹就会更平滑。
3. 归一化时间参数

轨迹规划中容易出现一些数值问题，比如需要求t的高阶指数，如果t比较大，计算数值就会很大，而且最终轨迹的参数会很小，特别是高阶项系数，比如很有可能小于float的精度，所以一般计算过程中最好用double。
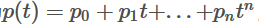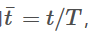但还有一种办法，是把轨迹参数做时间归一化，将时间归一化到[0,1]之间。设未归一化的轨迹为，令时间，则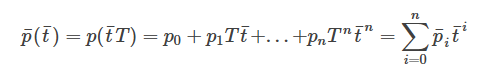

其中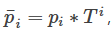，，T为轨迹总时间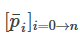，就是归一化时间的轨迹参数，它们不会像非归一化参数那么小，便于参数传递。

归一化参数如何求pva？

对于任一时刻t，先除以总时间T得到归一化时间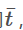

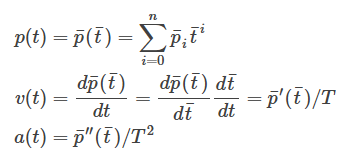
注意：归一化事件参数后，位置计算和原来相同，但速度计算需要除以T，加速度需要除以T²，即每求一阶导需要除以一个T。

实验过程中，用Matlab求解，如果一开始就用归一化时间参数，会解不出来，不知为何？所以，在求解过程中，仍然用的非归一化时间参数，而求解完以后，参数传递出去时，转换成归一化时间参数。


参考链接：https://blog.csdn.net/q597967420/article/details/77623235