正则文法介绍
要了解正则表达式的原理,需要先了解一些计算机语言文法的基础知识。
一个文法可以用一个四元来定义,G = {Vt,Vn,S,P}
其中Vt是一个非空有限的符号集合,它的每个元素成为终结符号。Vn也是一个非空有限的符号集合,它的每个元素称为非终结符号,并且Vt∩Vn=Φ。S∈Vn,称为文法G的开始符号。P是一个非空有限集合,它的元素称为产生式。所谓产生式,其形式为α→β,α称为产生式的左部,β称为产生式的右部,符号“→”表示“定义为”,并且α、β∈(Vt∪Vn)*,α≠ε,即α、β是由终结符和非终结符组成的符号串。开始符S必须至少在某一产生式的左部出现一次。
文法可推导的语言标记为L(G)。
著名语言学家Chomsky(乔姆斯基)根据对产生式所施加的限制的不同,把文法分成四种类型,即0型、1型、2型和3型。
- 0型文法要求至少含有一个非终结符,基本没有什么限制,一个非常重要的理论结果是:0型文法的能力相当于图灵机
- 1型文法也叫上下文有关文法,对应于线性有界自动机,要求每个产生式α→β,都有|β|>=|α|,|β|指长度;
- 2型文法也叫上下文无关文法,对应于下推自动机,要求在1型文法的基础上,再满足:每一个α→β都有α是非终结符;
- 3型文法也叫正则文法,它对应于有限状态自动机。它是在2型文法的基础上满足:A→α|αB(右线性)或A→α|Bα(左线性)。
正则表达式就是最后一种,正则文法,的一种表达形式,以整个字母表作为终结符集合Vt。
假设有一个文法的产生式是{S->Sa; S->b;},那么对应的正则表达式为ba*。
因此正则表达式,正则文法,有限状态自动机这个三个概念虽然指不同的东西,但是具备内在的等价性。
正则表达式是正则文法,限制多于上下文无关文法,而我们使用的编程语言语法都是上下文无关文法,因此试图通过正则表达式去处理代码(比如语言翻译、代码生成)的努力极可能归于徒劳。不过,把代码当做纯文本,然后在处理过程中使用正则表达式,仍然能大大提高效率。
正则表达式的基础运算符
正则表达式包含很多的元字符来表达规则,不过本文不是要介绍如何使用正则表达式,关于正则表达式规则最好的参考书是《精通正则表达式》。
实际上,正则表达式核心的运算符只有以下几种:
| 名称 | 示例 | 备注 |
|---|---|---|
| 或运算 | r|s | 匹配的语言是L(r)和L(s)的并集 |
| 连接运算 | rs | 匹配的语言是L(r)和L(s)连接 |
| Kleene运算 | r* | 匹配的语言是L(r)和L(s)连接 |
| 括号 | (r) | 匹配的语言与L(r)一致 |
kleene运算符优先级最高,且是左结合的,连接第二,或运算优先级最低。
运算定律:
| 示例 | 备注 |
|---|---|
| r|s = s|r | | 运算满足交换律 |
| r|s|t = r|(s|t) | | 满足结合律 |
| r(st) | 连接可以结合 |
| r(s|t) = rs|rt | 连接对|可以分配 |
| ℇr = rℇ = r | ℇ是连接的单位元 |
| r* = (r|ℇ)* | 闭包中一定包含ℇ |
| r** = r* | *具有幂等性 |
扩展运算符使得正则表达式更具表达力,下面仅举几个例子:
| 扩展运算符 | 等价形式 |
|---|---|
| + | r+ = rr* = r*r |
| ? | r? = r | ℇ |
| 字符类 | [a1a2…an] = a1|a2|…|an;如果是连续的字符类,可以写成[a1-an] |
高级特性:
正则表达式具备很多高级特性,比如捕获、环视、固化分组等等,这些特性是为了提高正则表达式的实用价值被设计出来的,不属于正则文法的范畴。
NFA和DFA
前面说过,正则文法对应于有限状态自动机,又分确定型有限状态自动机(DFA)和非确定型有限状态自动机(NFA),这两种状态机的能力是一样的,都能识别正则语言。正则表达式的识别引擎,都是基于DFA或NFA构造的。关于状态机的基础理论,这里就不描述了,只要稍微有点印象,就不妨碍继续阅读。
-
NFA
一个字母可以标记离开状态的多条边,并且ℇ 也可以标记一条边;这说明NFA的匹配过程面临很多的岔路,需要做出选择,一旦某条岔路失败,就需要回朔。
下图是正则表达式(a|b)*abb对应的NFA,它相当直观,基本可以从正则表达式直接转换而来。
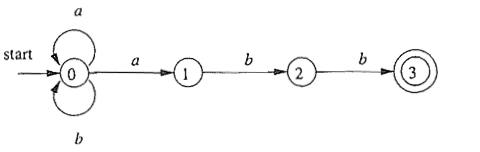
-
DFA
对于每个状态以及字母表中的每个字母,只能有一条以该字母为标记的,离开该状态的边;这说明DFA的匹配过程是确定的,每个字母是需要匹配一次。
与上面NFA等价的DFA如下图,相当地不直观:

- 将NFA转化成DFA
由于NFA和DFA的能力是一样的,每个NFA必然可以转化成一个等价的DFA。既然DFA对每个输入可以到达的状态时是确定的,那么输入串s在NFA中可能达到的状态集合对应为等价DFA中某个状态。从这个思路出发,可以构造出DFA。
- 首先NFA的初始状态0不接受ℇ ,因此可以构造出DFA的初始状态(0);
- 集合(0)输入a,在NFA中能够到达(0,1),于是构造出此状态,以及从(0)到(0,1)的边,标记为a
- 集合(0)输入b,能到到达的还是(0),因此构造出从(0)到自身的一条标记为b的边
- 集合(0,1)输入a,能能够到达的还是(0,1),与上一步类似
- 集合(0,1)输入b,能够给到达的是(0,2),构造状态(0,2)及相应的边
- 集合(0,2)输入a, 能够到达(0,1),没有新状态,添加一条边
- 集合(0,2)输入b,能够给达到(0,3),构造新状态(0,3)
- 集合(0,3)输入a,能够到达(0,1),添加一条边即可
- 集合(0,3)输入b,能够给达到(0),添加一条边即可
- 没有新状态,结束
最终得到的DFA如下,(0,3)包含了NFA的终结状态3,因此也是DFA的中介状态,对状态重新命名可以得到上面同样的DFA。
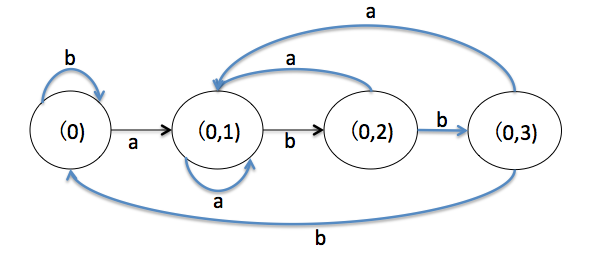
-
DFA和NFA的效率差异
很容易理解,构造DFA的代价远大于NFA,假设NFA的状态数为K,那么等价DFA的状态数目理论上可达2的k次方,不过实际上几乎不会出现这么极端的情况,可以肯定的是构造DFA会消耗更多的时间和内存。
但是DFA一旦构造好了之后,执行效率就非常理想了,如果一个串的长度是n,那么匹配算法的执行复杂度是O(n);而NFA在匹配过程中,存在大量的分支和回朔,假设NFA的状态数为s,因为每输入一个字符可能达到的状态数做多为s,那么匹配算法的复杂度及时输入串的长度乘以状态数O(ns)。
正则表达式的NFA&DFA构造、转化、简化有一整套理论及方法,远比上面的例子复杂,本文仅通过一个简单的例子来说明原理。
NFA与DFA的能力差异
NFA和DFA这两种匹配算法,除了效率上的差别外,从更高的视点看,形成了两种风格的引擎,进而对正则表达式的匹配的其他方面能力造成差异。NFA被称之为"表达式主导"引擎,而DFA被称之为“文本主导”引擎。
NFA:表达式主导
从表达式的第一个部分开始,每次检查一部分,同时检查当前文本是否匹配表达式的当前部分,如果是,则继续表达式的下一部分,如此继续,直到表达式的所有部分都能匹配,即整个表达式匹配成功。
我们来看表达式to(nite|knight|night)匹配文本...tonight...的过程: 表达式的第一个部分是t,它会不断重复扫描,直到在字符串中找到t,之后就检查随后的o,如果能匹配就继续检查下面的元素。这个例子中,下面的元素是(nite|knight|night),意思是nite或者knight或者night,引擎会依次尝试这三种可能。
整个过程,控制权在表达式的元素之间转换,因此被称之为“表达式主导”。“表达式主导”的特点是每个子表达式都是独立的,不存在内在联系。 子表达式与整个正则表达式的控制结构(多选、量词)的层级关系控制了整个匹配过程。
DFA:文本主导
DFA在读入一个文本的时候,会记录当前有效的所有匹配的表达式位置(这些位置集合对应于DFA的一个状态)。
以上面的匹配过程为例:
- 当引擎读入文本t时,记录匹配的位置是to(nite|knight|night);
- 接着读入o,匹配位置to(nite|knight|night);
- 读入n,匹配位置to(nite|knight|night),两个位置,knight被淘汰出局;
- ...
这种方式被称之“文本主导”是因为被扫描的字符串,控制了引擎的执行过程。
差异之一:NFA表达式影响引擎
NFA表达式主导的特性,使得通过修改正则表达式来影响引擎,因此下面三个表达式尽管能够匹配同样的文本,但是引擎的执行过程各不相同:
- to(nite|knight|night)
- tonite|toknight|tonight
- to(k?night|nite)
但是对于DFA来说,没有任何区别。
差异之二:DFA能保证最长匹配
对于包含或选项的表达式,NFA在成功匹配一个选项之后可能报告匹配成功,此时并不知道后面的选项是否也会成功,是否包含一个更长的匹配。
假设使用one(self)?(selfsufficient)?来匹配oneselfsufficient,NFA首先匹配one,然后匹配self,此时发现selfsufficient无法匹配剩余子串,但是这个子表达式不是必须的,因此可以立即返回成功,此时匹配的串为oneself。
实际上NFA引擎的匹配结果与具体实现有关,而DFA必然会成功匹配oneselfsufficient。
差异之三:NFA支持更多功能
NFA能够支持“捕获group”,“环视”,“占有优先量词”,“固话分组”等高级功能,这些功能都基于“子表达式独立进行匹配”这一特点。 而DFA无法记录匹配历史与子表达式之间的关系,因而也无法实现这些功能。
可见NFA引擎具备更大的实用价值,因而,我们在编程语言里面使用的正则表达式库都是基于NFA的。java的Pattern就是基于NFA的,Pattern.compile()方法显然就是在构造NFA状态图。
参考资料
- 《精通正则表达式》
- 《编译原理龙书第二版》