1.4.25扔两个鸡蛋。和上一题相同的问题,但现在假设你只有两个鸡蛋,而你的成本模型则是扔鸡蛋的次数。设计一种策略,最多扔2sqrt(N)次鸡蛋即可判断出F的值,然后想办法把这个成本降低到~c.sqrt(F)次。这和查找命中(鸡蛋完好无损)比未命中(鸡蛋被摔碎)的成本小得多的情形类似。
答:
1)~2sqrt(N)次的算法是:约分成sqrt(N)个组,每组sqrt(N)层,先用一个蛋从每组的最高层向上抛,蛋碎后确定所在的层,然后从上一组的第一层逐层向上抛另一个蛋,直到碎为止,从而确定F的值。
2)抛~c√F次蛋的算法:
2.1)首先蛋不能从高层开始抛,碎了一个蛋后剩下的一个蛋就只能逐层抛。
2.2)√F次就是一个提示信息。
依据以上两点,设(k-1)^2<F<=k^2,在k^2层抛时碎一个蛋,由此得出确定F所在的区间需要进行k次抛蛋,由于F<=k^2,所以√F≅k,所以确定F所在的区间需要√F次抛蛋。在确定区间后,需要在(K-1)^2~k^2区间内从低到高逐层抛第二个蛋以确定F的精确值,此区间抛蛋次数为k^2-(k-1)^2=2k-1次,2k-1≅2k≅2√F,所以在区间内确定F的精确值最多需要进行约2√F,那么确定区间和在区间内确定精确F值的抛蛋次数约为3√F。
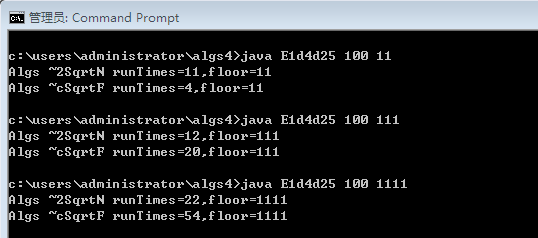
public class E1d4d25
{
public static void rank2SqrtN(int M,int f)
{
if(M*M<1) return;
if(f<1) return;
if (f>M*M) return;
//
int x=0;
int runTimes=0;
while(x<=M*M && x<f)
{
x=x+M;
runTimes++;
}//end while
int floor=x-M+1;
while(floor<f)
{
floor++;
runTimes++;
}
StdOut.printf("Algs ~2SqrtN runTimes=%d,floor=%d ",runTimes,floor);
return ;
}//end rank
public static void rankCSqrtF(int N,int f)
{
int k=1;
int runTimes=0;
while(k*k<f)
{
k++;
runTimes++;
}
//
int i=(k-1)*(k-1)+1;
while (i<f)
{
i++;
runTimes++;
}
StdOut.printf("Algs ~cSqrtF runTimes=%d,floor=%d ",runTimes,i);
}
public static void main(String[] args)
{
int M=Integer.parseInt(args[0]);
int f=Integer.parseInt(args[1]);
rank2SqrtN(M,f);
rankCSqrtF(M*M,f);
}
}
答:
1)~2sqrt(N)次的算法是:约分成sqrt(N)个组,每组sqrt(N)层,先用一个蛋从每组的最高层向上抛,蛋碎后确定所在的层,然后从上一组的第一层逐层向上抛另一个蛋,直到碎为止,从而确定F的值。
2)抛~c√F次蛋的算法:
2.1)首先蛋不能从高层开始抛,碎了一个蛋后剩下的一个蛋就只能逐层抛。
2.2)√F次就是一个提示信息。
依据以上两点,设(k-1)^2<F<=k^2,在k^2层抛时碎一个蛋,由此得出确定F所在的区间需要进行k次抛蛋,由于F<=k^2,所以√F≅k,所以确定F所在的区间需要√F次抛蛋。在确定区间后,需要在(K-1)^2~k^2区间内从低到高逐层抛第二个蛋以确定F的精确值,此区间抛蛋次数为k^2-(k-1)^2=2k-1次,2k-1≅2k≅2√F,所以在区间内确定F的精确值最多需要进行约2√F,那么确定区间和在区间内确定精确F值的抛蛋次数约为3√F。

public class E1d4d25
{
public static void rank2SqrtN(int M,int f)
{
if(M*M<1) return;
if(f<1) return;
if (f>M*M) return;
//
int x=0;
int runTimes=0;
while(x<=M*M && x<f)
{
x=x+M;
runTimes++;
}//end while
int floor=x-M+1;
while(floor<f)
{
floor++;
runTimes++;
}
StdOut.printf("Algs ~2SqrtN runTimes=%d,floor=%d ",runTimes,floor);
return ;
}//end rank
public static void rankCSqrtF(int N,int f)
{
int k=1;
int runTimes=0;
while(k*k<f)
{
k++;
runTimes++;
}
//
int i=(k-1)*(k-1)+1;
while (i<f)
{
i++;
runTimes++;
}
StdOut.printf("Algs ~cSqrtF runTimes=%d,floor=%d ",runTimes,i);
}
public static void main(String[] args)
{
int M=Integer.parseInt(args[0]);
int f=Integer.parseInt(args[1]);
rank2SqrtN(M,f);
rankCSqrtF(M*M,f);
}
}