题目:https://suctf.xctf.org.cn/contest_challenge/
答案:https://www.anquanke.com/post/id/146419#h3-23
MISC:
sandgame:
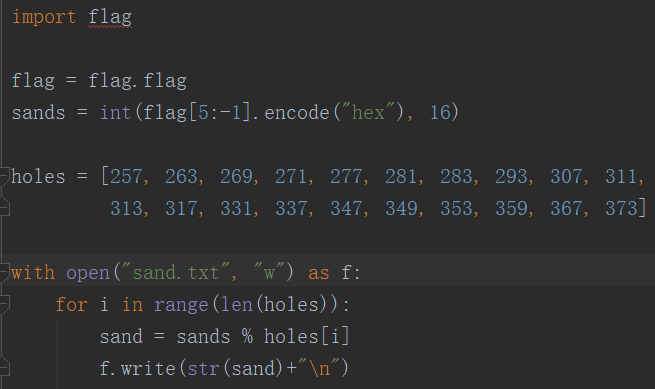
sand.txt :
222
203
33
135
203
62
227
82
239
82
11
220
74
92
8
308
195
165
87
4
转载来自:http://keep.01ue.com/?pi=370282&_a=app&_c=index&_m=p
题目很明确 就是同余方程组,只是20个同余式联立。考虑中国剩余定理,本来想写个程序,但是感觉太麻烦...(很有可能编不出来) 直接找工具。
Matlab好像没有算同余这种的,转手mathematica,调用ChineseRemainder,游戏结束:
百度:Mathematica 和 MATLAB、Maple 并称为三大数学软件。
另一种方法:
1 import gmpy2 as gm 2 def crack(): 3 holes = [257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373] 4 remains = [] 5 with open("sand.txt") as f: 6 line = f.readline().strip() 7 while line: 8 remains.append(int(line)) 9 line = f.readline().strip() 10 #提供一个在gmpy2下可以运行的数 11 M = gm.mpz(1) 12 for hole in holes: 13 #因为hole下全为质数,所以最小公倍数为全部相乘 14 M = M * hole 15 m = [] 16 m_inv = [] 17 for i in range(len(holes)): 18 #这个for循环求各个数对应基础数 19 #首先用最小公倍数除以holes的各个数 20 m.append(M / holes[i]) 21 #invert方法返回一个y,使m[i] + y = 1(mod holes[i]) 22 #通过乘法逆元得到基础数 23 #一个数与一个数的乘法逆元相乘(在mod p下)结果一定为一 24 m_inv.append(gm.invert(m[i], holes[i])) 25 re = gm.mpz(0) 26 for i in range(len(holes)): 27 #被除数与除数相乘,余数为1,那么除数不变,被除数扩大n倍,余数也一定扩大n被 28 #m[i]与m_inv相乘(在mod holes[i]下)结果为1,那么放大remains[i]倍后结果也会是remains[i] 29 re = re + m[i] * m_inv[i] * remains[i] 30 #求出re/M的余数 31 #因为M是holes列表中所有数的最小公倍数 32 re = gm.f_mod(re, M) 33 #将数字转换成16进制字符串,并把开头的0x去掉 34 print ("flag{" + hex(re)[2:].decode("hex") + "}") 35 36 37 if __name__ == "__main__": 38 crack()
Game:
Bash game, :https://blog.csdn.net/qq_41225779/article/details/79786815
巴什博弈:
n个物品,两个人每人每次可以取m~k个物品,最后取完的人获胜,输入n,m,k,问先手能否获胜。
(m当然不能为零,不然谁都不取,游戏就玩不下去了)
Wythoff game:https://blog.csdn.net/kongming_acm/article/details/5871249
威左夫博弈:
有两堆石子,数量任意,可以不同。游戏开始由两个人轮流取石子。游戏规定,每次有两种不同的取法,一是可以在任意的一堆中取走任意多的石子;二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。
Nim Game:https://www.cnblogs.com/wchyi/p/5551434.html
一张纸上,画若干条线,双方一人划一次,每次划掉1~3条线。可以选择画1条,也可以划2条,也可以3条。具体划去几条线完全看自己的策略。谁划掉最后一条线,就是赢家。
-----pwn(转载):https://blog.csdn.net/gyhgx/article/details/53439417
RSA(可参考博客:https://www.cnblogs.com/my-mind/articles/9578491.html
题目下载下来后是一串代码
1 import random 2 import hashlib 3 4 def invmod(a, n): 5 t = 0 6 new_t = 1 7 r = n 8 new_r = a 9 while new_r != 0: 10 #整除符号,联想到辗转相除法 11 q = r // new_r 12 (t, new_t) = (new_t, t - q * new_t) 13 (r, new_r) = (new_r, r - q * new_r) 14 if r > 1: 15 raise Exception('unexpected') 16 if t < 0: 17 t += n 18 return t 19 20 smallPrimes = [2, 3, 5, 7, 11, 13, 17, 19] 21 22 #判断一个数是否能和smallPrimes里的数整除 23 def primefactor(p): 24 for x in smallPrimes: 25 if p % x == 0: 26 return True 27 return False 28 29 def isprime(p, n): 30 for i in range(n): 31 #返回闭区间[1,p]范围内的整数 32 a = random.randint(1, p) 33 #这里求出a ** p-1 mod p 34 if pow(a, p - 1, p) != 1: 35 return False 36 return True 37 38 def getprime(bit): 39 while True: 40 #p是在2的bit-1次方和2的bit次方-1范围内的整数 41 p = random.randint(2**(bit - 1), 2**bit - 1) 42 #当p不能被2,3,5,7,11,13,17,19整除,且在1到p的范围内存在数a,使a ** p-1 mod p = 1成立 43 if not primefactor(p) and isprime(p, 5): 44 return p 45 46 def genKey(keybits): 47 e = 3 48 # // 为整除符号,即取商的整数部分 49 #传入的参数为2048,得出的结果即1025 50 bit = (keybits + 1) // 2 + 1 51 52 p = 7 53 while (p - 1) % e == 0: 54 p = getprime(bit) 55 56 q = p 57 while q == p or (q - 1) % e == 0: 58 q = getprime(bit) 59 #RSA加密的公钥和私钥的生成 60 n = p * q 61 et = (p - 1) * (q - 1) 62 d = invmod(e, et) 63 pub = (e, n) 64 priv = (d, n) 65 66 return (pub, priv) 67 68 69 70 pub, priv = genKey(2048) 71 (e,n) = pub 72 (d,n) = priv 73 de_hash = set() 74 75 76 77 def b2n(s): 78 #将bytes[]转换为int类型的数据 79 return int.from_bytes(s, byteorder='big') 80 81 def n2b(k): 82 #将int类型的数据转换为bytes[]数组 83 return k.to_bytes((k.bit_length() + 7) // 8, byteorder='big') 84 85 def decrypt(cipher): 86 md5 = hashlib.md5() 87 md5.update(cipher) 88 digest = md5.digest() 89 if digest in de_hash: 90 raise ValueError('Already decrypted') 91 de_hash.add(digest) 92 #将密文转换为数字a,计算a ** d mod n 93 return n2b(pow(b2n(cipher), d, n)) 94 95 if __name__ == '__main__': 96 plain = "abc" 97 plain = plain.encode("utf-8") 98 #将明文转换为数字a,计算a ** e mod n 即RSA的公钥加密 99 cipher = n2b(pow(b2n(plain), e, n)) 100 #r是在2到n-1之间的一个随机整数 101 r = random.randint(2, n - 1) 102 #将密文转换为int数据 103 c = b2n(cipher) 104 105 c2 = (pow(r, e, n) * c) % n 106 print("e=",e) 107 print("d=",d) 108 print("c2=",c2) 109 print("r=",r) 110 print("n=", n)
(源代码我略微有些改动,与下载下来的有些许出入)
直接运行后会打印出e,d,c2,r,n的值
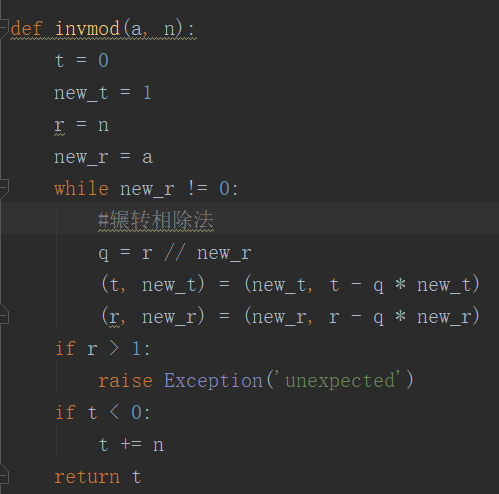

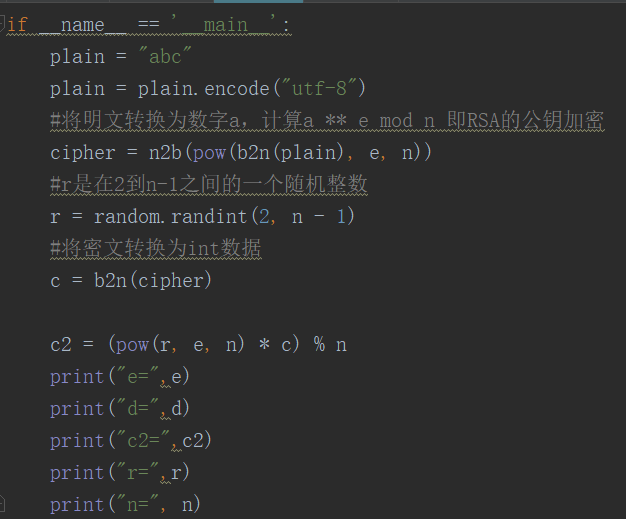

c2为多重加密最终得到的密文
然后再次使用python
1 import random 2 import binascii 3 import hashlib 4 from binascii import * 5 6 7 8 def invmod(a, n): 9 t = 0 10 new_t = 1 11 r = n 12 new_r = a 13 while new_r != 0: 14 q = r // new_r 15 (t, new_t) = (new_t, t - q * new_t) 16 (r, new_r) = (new_r, r - q * new_r) 17 if r > 1: 18 raise Exception('unexpected') 19 if t < 0: 20 t += n 21 return t 22 23 def b2n(s): 24 return int.from_bytes(s, byteorder='big') 25 26 def n2b(k): 27 return k.to_bytes((k.bit_length() + 7) // 8, byteorder='big') 28 29 30 def debytes(n,d,cbytes): 31 c = b2n(cbytes) 32 m = pow(c, d, n) 33 return n2b(m) 34 35 if __name__ == '__main__': 36 n = 66149493853860125655150678752885836472715520549317267741824354889440460566691154181636718588153443015417215213251189974308428954171272424064509738848419271456903929717740317926997980290509229295248854525731680211522487069759263212622412183077554313970550489432550306334816699481767522615564029948983958568137620658877310430228751724173392407096452402130591891085563316308684064273945573863484366971922314948362237647033045688312629960213147916734376716527936706960022935808934003360529947191458592952573768999508441911956808173380895703456745350452416319736699139180410176783788574649448360069042777614429267146945551 37 e = 3 38 d = 44099662569240083770100452501923890981810347032878178494549569926293640377794102787757812392102295343611476808834126649538952636114181616043006492565612847637935953145160211951331986860339486196832569683821120141014991379839508808414941455385036209313700326288366870889877799654511681743709353299322639045424737161223404842883211346043467541833205836604553399746326181139106884008412679110817142624390168364685584282908134947826592906891361640349523847551416712367526240125746834000852838264832774661329773724115660989856782878284849614002221996848649738605272015463464761741155635215695838441165137785286974315511355 39 c2 = 44072159524363345025395860514193439618850855989758877019251604535424645173015578445641737155410124722089855034524900974899143590319109150794463017988146330700682402644722045151564192212786022295270147246354021288864468319458821200111865992881657865302651297307278194354152154089398262689939864900434490148230032752585607483545643297707980226837109082596681204037909705850077064452350740011904984407745294229799642805761872912116003683053767810208214723900549369485228083610800628462169538658223452866042552036179759904943895834603686937581017818440377415869062864539021787490351747089653244541577383430879642738738253 40 r = 45190871623538944093785281221851226180318696177837272787303375892782101654769663373321786970252485047721399081424329576744995348535617043929235745038926187396763459008615146009836751084746961130136655078581684659910694290564871708049474081354336784708387445467688447764440168942335060081663025621606012816840929949463114413777617148271738737393997848713788551935944366549647216153686444107844148988979274170780431747264142309111561515570105997844879370642204474047548042439569602410985090283342829596708258426959209412220871489848753600755629841006861740913336549583365243419009944724130194890707627810912114268824770 41 42 cipher2 = n2b(c2) 43 plaintext3 = debytes(n,d,cipher2)#第一次解密 44 print (plaintext3)
45 p3 = b2n(plaintext3) 46 p4 = (p3 * invmod(r, n)) % n #第二次解密 47 plaintext4 = n2b(p4) 48 print (plaintext4)

获得flag
-------------------------------------------------------------------
辗转相除法:
|
a
|
b
|
a mod b
|
|
123456
|
7890
|
5106
|
|
7890
|
5106
|
2784
|
|
5106
|
2784
|
2322
|
|
2784
|
2322
|
462
|
|
2322
|
462
|
12
|
|
462
|
12
|
6
|
|
12
|
6
|
0
|